经典网文分享

实分析Ⅱ|笔记整理（5）——非负可测函数积分

同学们好！

大家是不是看到这个标题感到不太陌生呢？

这一部分内容开始我们开始关注实分析中的积分部分。这一部分和Stein也有部分的重合度，所以按照老办法，我们对于重复的部分只会简单地提一下。

因为ZH在五一期间出现了专栏的bug导致之前的笔记丢失，损失惨重，因此我想了一些补救方案，写在了这篇文章上：

刘理：杂烩|2018.5-近期情况说明，相关typo修改

提供之前的笔记（注意目录顺序……）：

我们开始本节的内容，本节所含原书内容为P131-

非负简单可测函数的积分

从这里开始考虑的原因是简单可测函数逼近定理（原书定理3.9）。

Definition 1:
设 $f(x)$ 为 $\mathbb{R}^n$ 上的非负可测简单函数，它在点集 $A_i(i=1,2,...,p)$ 上取值为 $c_i$ ，并且 $f(x)=\sum_{i=1}^{p}c_i\chi _{A_i}(x),\bigcup_{i=1}^{p}A_i=\mathbb{R}^n,A_i \cap A_j = \emptyset(i \ne j)$ 。若 $E \in \mathcal{M}$ ，那么定义 $f(x)$ 在 $E$ 上的积分为 $\int_{E}f(x)dx=\sum_{i=1}^{p}c_im(E\cap A_i)$ 。

这一块定义和Stein稍显不同。

下面是相关的性质。

Theorem 1:
设 $f(x),g(x)$ 为 $\mathbb{R}^n$ 上的非负可测简单函数， $f(x)$ 在点集 $A_i(i=1,\cdots,p)$ 上取值为 $a_i$ 。 $g(x)$ 在点集 $B_j$ 上取值为 $b_j$ ， $E \in \mathcal{M}$ ，则
(1)若 $C$ 是非负常数，那么 $\int_E Cf(x)dx=C \int_E f(x)dx$
(2) $\int_E (f(x)+g(x))dx=\int _E f(x)dx+\int _E g(x)dx$

（请注意，这里的 $dx$ 写法不规范，应该是 $\mathrm{d}x$ ，这里为节省时间）

只证明第二个，因为 $f(x)+g(x)$ 在 $A_i \cap B_j$ 上取值 $a_i+b_j$ （当然了， $A_i \cap B_j$ 是空集其实是不影响的），那么有 $\int_E (f(x)+g(x))dx=\sum_{i=1}^{p}\sum_{j=1}^{q}(a_i+b_j)m(E \cap A_i \cap B_j)$ 拆分可得 $\sum_{i=1}^{p}\sum_{j=1}^{q}(a_i+b_j)m(E \cap A_i \cap B_j)=\sum_{i=1}^{p}a_i\sum_{j=1}^{q}b_jm(E \cap A_i \cap B_j)+\sum_{j=1}^{q}b_j\sum_{i=1}^{p}a_im(E \cap A_i \cap B_j)$ 然后，注意到 $\sum_{j=1}^{q}m(E \cap A_i \cap B_j)=m(E \cap A_i)$ （这是因为 $\bigcup_{i=1}^{p}A_i=\mathbb{R}^n$ 和可数可加性），同理得到 $\sum_{i=1}^{p}m(E \cap A_i \cap B_j)=m(E \cap B_j)$ ，所以化简可得上式即为 $\sum_{i=1}^{p}a_im(E \cap A_i)+\sum_{j=1}^{q}b_jm(E \cap B_j)$ ，这也就是 $\int_E f(x)dx+\int _E g(x)dx$ 。

事实上，还有一个性质就是Stein里所说的"积分的值与表示无关"。这里Stein里说的比较清楚，所以就不再在这里赘述了。

下一个小定理也是之前对我们学过的知识的一个简单应用。

Theorem 2:
若 $\{E_k\}$ 为 $\mathbb{R}^n$ 中的递增可测集列， $f(x)$ 为 $\mathbb{R}^n$ 上的非负可测简单函数，则 $\int_E f(x)dx=\lim_{k \to \infty} \int_{E_k}f(x)dx,E = \bigcup_{k=1}^{\infty}E_k$

事实上，只需要走定义，根据 $\lim_{k \to \infty}\int _{E _k}f(x)dx=\lim_{k \to \infty}\sum_{i=1}^{p}c_i m(E_k \cap A_i)=\sum_{i=1}^{p}c_im(E \cap A_i)$ （原书定理2.8）即可得。

非负可测函数的积分

根据简单函数的积分，我们给出非负可测函数积分的定义。

Definition 2:
设 $f(x)$ 为 $E \subset \mathbb{R}^n$ 上的非负可测函数，定义 $f(x)$ 在 $E$ 上的积分为 $\int_E f(x)dx=\sup _{\substack{h(x) \le f(x) \\ x\in E} }\{\int _E h(x)dx:h(x)是\mathbb{R}^n上的非负可测简单函数\}$ ，如果 $\int_E f(x)dx<+\infty$ ，则称 $f(x)$ 在 $E$ 上可积。

一个简单的事实是

$f(x) \le g(x)(x \in E ),f(x),g(x) \ge 0$ ，则 $\int_E f(x)dx \le \int _E g(x)dx$

我们不再证明。

另外，根据这个定义还可以推出两个有趣的性质。

Proposition 1:
(1)若 $f(x)$ 为 $E$ 上的非负可测函数， $A$ 是 $E$ 中可测子集，那么 $\int_A f(x)dx=\int_E f(x)\chi_A(x)dx$
(2)若 $f(x)$ 在 $E$ 上几乎处处为0，那么 $\int_E f(x)dx=0$ ，反之亦然。

对于第一个，注意到 $\int_A f(x)dx=\sup_{\substack{h(x) \le f(x) \\ x \in A}}\{\int_A h(x)dx\}=\sup_{\substack{h(x)\chi_A(x)\le f(x)\chi_A(x) \\ x \in E }}\{\int_A h(x)dx\}$ 即可。

对于第二个，一方面，如果在 $E$ 上 $f(x)$ 几乎处处为0，那么设 $Z=\{x \in E : f(x)=0\}$ ，则 $m(Z)=0$ 。这样的话 $\int_Ef(x)dx=\int_Zf(x)dx+\int_{E \setminus Z}f(x)dx$ （Stein里提了这个性质，事实上用这里的定义证明，也不是难事）。一部分函数值是0，一部分是基于零测集上的积分，那么自然容易得到这个积分值就是0。

另一方面，如果 $\int_E f(x)dx=0$ ，考虑构造 $E_k=\{x \in E: f(x) > 1/k\}$ ，那么只需要根据 $\int_E f(x)dx \ge \int _{ E_k}f(x)dx \ge \int_{E_k}\frac1k dx=\frac1k m(E_k)$ 即可得到 $m(E_k)=0(k=1,2,\cdots)$ 。接着根据 $\{x \in E : f(x)>0\}=\bigcup_{k=1}^{\infty}E_k$ 即可得到 $m(\{x \in E : f(x)>0\})=0$ 。

下面这个依然是一个小定理，但是结论非常重要，也很直观。

Theorem 3:
若 $f(x)$ 为 $E$ 上的非负可积函数，则 $f(x)$ 在 $E$ 上几乎处处有限。

谈到"几乎处处有限"，想也不用想就是构造 $E_k=\{x \in E : f(x) >k\}$ ，则 $\{x \in E : f(x)=+\infty\}=\bigcap_{k=1}^{\infty}E_k$ 。结合 $\int_E f(x)dx \ge \int_{E_k} f(x)dx \ge km(E_k)$ 与 $\int_E f(x)dx < +\infty$ 即可得到 $\lim_{k \to \infty} m(E_k)=0$ 。别忘了 $\{E_k\}$ 是递减列，所以自然有 $m(\{x \in E : f(x) =+ \infty\})=0$ 。

接下来这个定理是一个比较重要的大定理，以后我们可能会经常用到它。

Theorem 4:Beppo Levi
设有定义在 $E$ 上的非负可测函数渐升列 $f_1(x) \le f_2(x) \le \cdots \le f_k(x) \le \cdots$ 且有 $\lim_{ k \to \infty}f_k(x)=f(x), x \in E$ ，那么有 $\lim_{k \to \infty}\int _E f_k(x)dx=\int_E f(x)dx$

首先，由渐升列的定义，容易得到 $\lim_{k \to \infty}\int_E f_k(x)dx$ 有定义，积分 $\int_E f(x)dx$ 有定义（有定义是根据 $f(x)$ 非负可测得到的，要注意它和可不可积并不是一个概念）。并且还是根据渐升列可以直接得到 $\lim_{k \to \infty}\int_E f_k(x)dx \le \int_E f(x)dx$ （某一项是小的，你取极限后自然还是小的）。

下面考虑另外一个方向。因为要证明 $\int_E f(x)dx$ 是小于左边的式子的，所以自然的要考虑非负可测简单函数 $h(x)$ （通过任意一个 $h(x)$ 的估计和积分的定义，自然可以得到 $f(x)$ 的估计）。考虑到渐升列，构造集合 $E_k=\{x \in E : f_k(x) \ge ch(x)\}(k=1,2,\cdots)$ ，其中 $0<c<1$ 任意取定。这样的话 $\{E_k\}$ 递增可测，所以根据Theorem 2可得 $\lim_{k \to \infty}c\int_{E_k}f_k(x)dx = c \int_E h(x)dx$ 。又容易得到 $\int_E f_k(x)dx \ge c\int_{E_k}h(x)dx$ ，两边取极限，令 $c \to 1$ ，可以得到 $\lim_{k \to \infty}\int_E f_k(x)dx \ge \int_E h(x)dx$ 。最后因为 $h(x)$ 是任意的，所以就可以得到 $\lim_{k \to \infty}\int_E f_k(x)dx \ge \int_E f(x)dx$ ，就证明了结论。

这个定理相当于说，如果函数是渐升列，那么它的积分和极限可交换。

这个定理的一个最直接的应用是之后的这个性质，因为有可交换性与简单函数逼近定理的保证，会让很多问题变得简单很多。

Theorem 5:
设 $f(x),g(x)$ 为 $E$ 上的非负可测函数， $\alpha,\beta$ 为非负常数，那么 $\int_E(\alpha f(x)+\beta g(x))dx=\alpha \int _E f(x)dx+\beta \int_E g(x)dx$

事实上根据简单函数逼近定理，结合Theorem 4可以把它转为非负可测简单函数的情况。具体的过程可以查看Stein，这里略去。

当然了，渐降列也是有类似的性质的

Proposition 2:
设 $\{f_k(x)\}$ 为 $E$ 上的非负可积函数渐降列，且 $\lim_{k \to \infty}f_k(x)=f(x), ~ a.e. x \in E$ ，那么 $\lim_{k \to \infty}\int_E f_k(x)dx = \int_E f(x)dx$ 。

简单说明一下，构造 $g_k(x)=f_1(x)-f_k(x)$ ，那么这就变成了一个渐升列，然后根据构造出的渐升列可得 $\lim_{k \to \infty}\int_E(f_1(x)-f_k(x))dx=\int_E(f_1(x)-f(x))dx$ 。另一方面，根据积分的线性性质，再取极限，可得 $\lim_{k \to \infty}(\int_E f_1(x)dx-\int_E f_k(x)dx)=\int_E(f_1(x)-f(x))dx=\int_E f_1(x)dx - \int_E f(x)dx$ 。这样的话，把左边取极限的部分拆开，消去有限项（可积）即可得结论（别忘了 $f_1(x)$ 在取极限的时候是不受影响的）。

之后要说的逐项积分定理，其证明将运用Beppo Levi定理，而它本身也很重要。

Theorem 6:
若 $\{f_k(x)\}$ 是 $E$ 上非负可测函数列，那么 $\int_E \sum_{k=1}^{\infty}f_k(x)dx=\sum_{k=1}^{\infty}\int_Ef_k(x)dx$

令 $S_m(x)=\sum_{k=1}^{m}f_k(x)$ ，那么就构造出了一个渐升列，并且 $\lim_{m \to \infty}S_m(x)=\sum_{k=1}^{\infty}f_k(x)=S(x)$ 。这样的话，注意到左边就相当于 $\int_E S(x)dx$ ，所以只要证明右边是 $\lim_{m \to \infty}\int \sum_{k=1}^{m}f_k(x)dx$ 即可。而右边化一下极限可得 $\sum_{k=1}^{\infty}\int_Ef_k(x)dx=\lim_{m \to \infty}\sum_{k=1}^{m}\int_E f_k(x)dx$ 。之后只要根据积分的线性性质即可得到结论。

一个简单的推论如下：

Corollary 1:
设 $E_k \in \mathcal{M}(k=1,2,\cdots)$ ， $E_i \cap E_j=\emptyset(i \ne j)$ ，若 $f(x)$ 为 $E=\bigcup_{k=1}^{\infty}E_k$ 上的非负可测函数，则 $\int_Ef(x)dx=\int_{\cup_{k=1}^{\infty}E_k}f(x)dx=\sum_{k=1}^{\infty}\int_{E_k}f(x)dx$

根据 $\int_{E_k}f(x)dx=\int_Ef(x)\chi_{E_k}(x)dx$ 和逐项积分定理即可得到结论，这里略去详细的证明。

这个推论主要的来源于测度的可数可加性，不过因为积分的存在，所以很多时候在测度的环境下也可以使用积分来估计。

下面一个例子说明了积分在测度的应用。

Example 1:
若 $E_1,E_2,\cdots, E_n$ 为 $[0,1]$ 中的可测集，且 $[0,1]$ 中每一点至少属于上述集合中的 $k$ 个，那么 $E_1,\cdots,E_n$ 中至少有一个点集的测度大于等于 $k/n$ 。

只需要注意 $\sum_{i=1}^{n}m(E_i)=\sum_{i=1}^{n}\int_{[0,1]}\chi_{E_i}(x)dx=\int_{[0,1]}\sum_{i=1}^{n}\chi_{E_i}(x)dx$ ，且根据 $\sum_{i=1}^{n}\chi_{E_i}(x) \ge k$ 可得到 $\int_{[0,1]}\sum_{i=1}^{n}\chi_{E_i}(x)dx \ge k$ 。所以如果任何一个点集测度小于 $k/n$ ，就可以得到 $\sum_{i=1}^{n}m(E_i) < \frac k n*n =k$ ，这就矛盾了。所以原定理自然是成立的。

下面引入Fatou引理。

Theorem 7: Fatou
若 $\{f_k(x)\}$ 是 $E$ 上的非负可测函数列，那么 $\int_E \underline{\lim}\limits_{k \to \infty}f_k(x)dx \le \underline{\lim}\limits_{k \to \infty}\int_E f_k(x)dx$

根据下极限的定义，考虑设 $g_k(x)=\inf \{f_j(x):j \ge k\}$ ，那么容易得到 $g_k(x) \le g_{k+1}(x)(k=1,2,\cdots)$ ，并且有 $\underline{\lim}\limits_{k \to \infty} f_k(x)=\lim_{k \to \infty}g_k(x), x\in E$ 。所以通过这种方式相当于构造了一个渐升列，根据相关定理可得 $\int_E \underline{\lim} \limits _{k \to \infty} f_k(x)dx=\lim_{k \to \infty}\int_E g_k(x)dx= \underline{\lim} \limits _{k \to \infty}\int_E g_k(x)dx \le \underline{\lim} \limits _{k \to \infty} \int _E f_k(x)dx$ （中间步骤是因为，极限存在那么下极限和极限相等），这就证明了结论。

书上给了一个函数 $f_n(x)=\begin{cases}0 & x =0 \\ n & 0<x<\frac1n \\ 0 & \frac1n \le x \le 1\end{cases}$ ，这个函数运用Fatou引理的话，其不等号是成立的。

最后是一个定理，引入了另外一种可积的充要条件，书上以它结束了这一节，我也打算这么做。

Theorem 8:
设 $f(x)$ 为 $E$ 上的几乎处处有限的非负可测函数， $m(E)<+\infty$ 。在 $[0,+\infty)$ 上作如下划分 $0=y_0<y_1<\cdots<y_k<y_{k+1}<\cdots \to \infty$ ，其中 $y_{k+1}-y_k<\delta(k=0,1,\cdots)$ ，若令 $E_k=\{x \in E : y_k \le f(x) < y_{k+1}\}(k=0,1,\cdots)$ ，则 $f(x)$ 在 $E$ 上可积当且仅当 $\sum_{k=0}^{\infty}y_km(E_k)<+\infty$ ，并且有 $\lim_{\delta \to 0}\sum_{k \to 0}^{\infty}y_km(E_k)=\int_E f(x)dx$

事实上，注意到 $y_km(E_k) \le \int_{E_k}f(x)dx \le y_{k+1}m(E_k)$ 就容易得到 $\sum_{k=0}^{\infty}y_km(E_k) \le \int_E f(x)dx \le \sum_{k=0}^{\infty}y_{k+1}m(E_k) \le \delta m(E)+\sum_{k=0}^{\infty}y_km(E_k)$ 。所以自然就可以得到结论成立（夹逼）

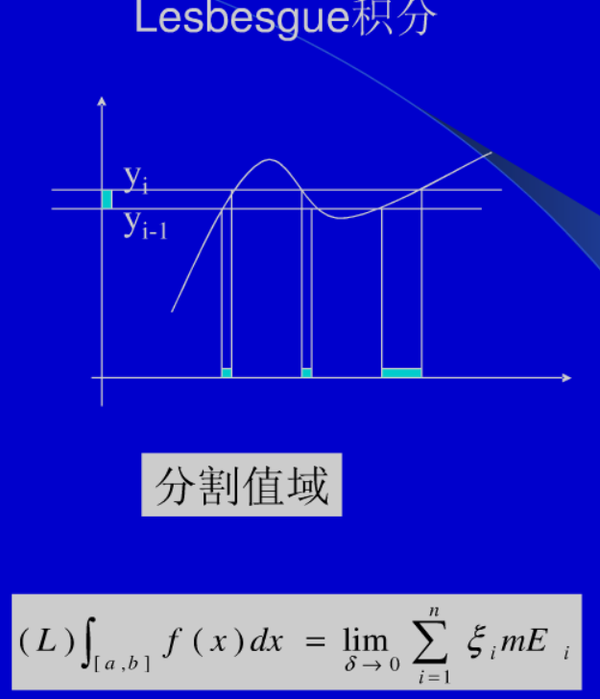
这个结论可以与Riemann积分相类比一下。Riemann积分是分割定义域来进行极限求和，而这里这个等价条件相当于是对值域进行相同的操作。

比方说，取 $E_k=\{x \in E : k \le f(x) < k+1\} (k=1,2,\cdots)$ ，那么 $f(x)$ 的可积性就等价于 $\sum_{k=1}^{\infty}km(E_k)<+\infty$ 。运用这个小结论，可以来解下面这个例子。

Example 2:
设 $E \subset \mathbb{R}:m(E)<+\infty$ , $f(x)$ 为 $E$ 上非负实值可测函数，那么 $f(x)$ 在 $[0,+\infty)$ 上可积的充要条件是 $\sum_{n=0}^{\infty}m(\{x \in E : f(x) \ge n\})<+\infty$

一方面，如果 $f(x)$ 可积，那么 $\sum_{n=0}^{\infty}m(\{x \in E : f(x) \ge n\})=\sum_{n=0}^{\infty}\sum_{k=n}^{\infty}m(\{x \in E : k \le f(x) <k+1\})$ $\sum_{k=0}^{\infty}(k+1)m(\{x \in E : k \le f(x) < k+1\}) < + \infty$ （第二步其实将求和号变一下即可，但要注意变换上下标为 $\sum_{k=0}^{\infty}\sum_{n=0}^{k}$ 。之后再用上面的结论）

另一方面，则只需要注意到 $\int_E f(x)dx=\sum_{k=0}^{\infty}\int_{\{x \in E : k \le f(x) <k+1\}}f(x)dx \le \sum_{k=0}^{\infty}(k+1)m(\{x \in E : k \le f(x) < k+1\}) < +\infty$ 即可知道结论成立（因为我偷懒省了最后一步……）

小结

这一节各位可能会想做一些吐槽，因为可能会感觉这一部分的内容没有什么太大的新意，也鲜有创新。不过确实我自己在看的时候发觉确实没有太多需要解释的部分，书上这一块写的很详细也很清楚。这当然对于所有人来说都是一件好事。

这一部分内容和Stein的观点和符号标记都稍有差别，因此我基本上没有省略掉原书的内容。这虽然一定程度上使笔记的内容多了不少，但是读者通过对比两本书的观点差异，其实还是可以发现很多有趣的东西的。

下一节我们会跟着原书的内容，继续介绍《实变函数论》中所涉及的一般函数积分的相关理论。

感谢大家一直以来的支持，为点赞收藏感谢赞赏的看客比心~~

——————————————————广告——————————————————

本专栏为我的个人专栏，也是我学习笔记的主要生产地。任何笔记都具有著作权，不可随意转载和剽窃。

想要更多方面的知识分享吗？欢迎关注专栏：一个大学生的日常笔记。我鼓励和我相似的同志们投稿于此，增加专栏的多元性，让更多相似的求知者受益~

来源：知乎 www.zhihu.com
作者：刘理

【知乎日报】千万用户的选择，做朋友圈里的新鲜事分享大牛。点击下载

先不谈杜兰特，火箭总得把应该做好的做好

这场是火箭视角的复盘，勇士视角复盘明天在公众号会发。

勇士VS火箭（G1）

勇士防守：

汤普森VS保罗，杜兰特VS哈登，库里VS阿里扎，伊戈达拉VS塔克，格林VS卡佩拉

火箭防守：

阿里扎VS库里，保罗VS汤普森，哈登VS伊戈达拉，塔克VS杜兰特，卡佩拉VS格林

全文核心内容，送给太长不看党：

初始对位存在问题，保罗这场防无球不佳；
哈登被库里找了N次，还被无球针对，火箭竟然无动于衷；
火箭固有的退防问题没有因为这是西决而改善；
锋线处理球和篮下终结差；
保罗带衔接段输给了勇士；
火箭的小个阵容有隐患。

勇士果然首发了死亡五小，首发对位还是与前瞻里的预测稍有出入。勇士直接让杜兰特对哈登——科尔好魄力——就像前瞻说的，这个对位的好处是哈登与卡佩拉挡拆，杜兰特和格林可以直接换防，其实就是直接断了哈卡挡拆的可能性。

但火箭的问题从对位就开始了。原本预期保罗会亲自对位库里，阿里扎对位汤神，这样体型上火箭吃亏少，结果火箭教练组让保罗去对汤普森，阿里扎对库里。火箭的意思可以理解为，库里更难防，为了给保罗减压，让阿里扎去对。

可问题就是，对位汤普森很轻松么？汤普森那跑动也累腿吧，保罗比汤神矮了快20厘米，汤神的无球掩护和背身翻身跳投，保罗都是干扰不到的——想想隆多是怎么被汤神射的。

火箭这赛季始终没能形成统一的防守对位规律，保罗和哈登的防守任务太奇怪了，第一轮就让横移吃亏的哈登对蒂格，身高吃亏的保罗对维金斯，但森林狼进攻选择能力全联盟最差没有之一，没能在这上面把文章做够，现在面对勇士就太冒险了。

保罗一些防无球失误

问题更大的是，保罗这场对汤神的盯防有点过于轻视，总是给汤神和尼克扬空位，不知道是怎么想的。

这个球，保罗站那愣神，汤神绕了一大圈没发现

保罗篮下去堵库里，给克莱那么大空位，库里的视野可不简单

同理，保罗衔接段对位尼克扬，还是放这么大，汤神突破分球的视野也不简单

可能是保罗这赛季总担任防守自由人的任务，协防习惯了，但对位克莱这个级别的射手，是不是应该给足尊重呢？如果保罗坚持要去协防，那么队友的轮转跟不上啊？

保罗和哈登还出现过换防交代不清的错误，库里挡拆找哈登，哈登想换，保罗没换，结果变成了夹击库里，放空尼克扬——最错误的防守策略就是夹击库里。

以保罗在江湖上的防守名望，这场比赛类似这种的防守失误是不能接受的。

哈登的防守问题

保罗的问题还只是小事，也相信他能在后面的比赛里自己调整，但哈登怎么办？哈登在火箭首发阵容里，防守能力是最差的，这没什么疑问，大部分时间也不是问题——米切尔找了无数次哈登，最终也没把火箭怎么样，毕竟爵士的空间不好，火箭篮下还有卡佩拉。

然而对手是勇士，库里来找哈登时，情况就不一样了——现在的现实就是，库里跟米切尔一样，过掉哈登这个步骤几乎不会失手，火箭想解决这个问题，就得在协防上想点办法，或者对位库里的球员努力挤过掩护，保护一下哈登，不让这个错位形成那么容易。可火箭完全没有保护哈登的意识，库里来找，火箭就换，卡佩拉又总是被格林或者卢尼调走，库里突进去基本就是上空篮，这就太离谱了。卡佩拉应该更警惕一些，当库里对哈登时，他应该随时放掉对位者去篮下协防。

火箭的退防

这些还只是阵地战的防守槽点，火箭的转换退防问题在G1比较集中的体现，退防总有1~2个球员回不来，而回来的球员又普遍矮，对攻框或者追身三分防不了，让勇士打转换有点太容易了——这些是一个赛季改不了的顽疾，没办法，卡佩拉和底角射手的站位太深，哈登突破上篮不中很多时候会倒地，回不来也正常。

卡佩拉刚回来，哈登还没回来，球已经打进了

但有些球，明明是多防少，还是莫名其妙被打进，火箭就该反思一下了，比如下面这个球，火箭回来五个人，可戈登和巴莫特找重了人，库里和杜兰特最后落位，就只能塔克扑库里，漏掉杜兰特了。

下面这个球就更离谱，保罗在前一个回合刚单打命中2分，勇士底线发球，然后库里一个长传球给前场的尼克扬，投进追身三分，时间只过了3秒，火箭没人管尼克扬...

这种理论上可以避免的退防失误，还是能少给就少给。

火箭锋线处理球和篮下终结能力差

火箭锋线单功能的问题，在大部分比赛里都不会有问题——灯泡能创造出足够好的机会，投空位三分他们都有能力把握。

可勇士的外线轮转扑的凶，有时候就需要火箭锋线多做一道处理，这就不是他们的强项了。前瞻里我写到，勇士要尽力轮转去扑火箭锋线，让他们多处理一次球，就多一次失误风险。这场球，巴莫特2个三分没进不是最大槽点，4个上篮全不进更伤人。

巴莫特这球放不进去？

巴莫特肩膀有伤，可以理解他终结出点问题，但阿里扎和塔克的表现也不好，阿里扎还有犯规麻烦。另外，勇士让库里对位阿里扎的效果还是体现出来了，哈登找库里连带着阿里扎从熟悉的底角位上提到45°和弧顶，他今天45°和弧顶三分球投了4个一个没进，火箭需要注意这点。

遭遇勇士扑防和篮下协防，火箭锋线处理球应该更聪明一点，例如塔克这个喂饼，结合他季后赛之前的表现，还是能看出他传球能力的长进。

巴莫特和阿里扎要进步啊...

保罗在衔接段输给了勇士

火箭衔接段在常规赛一直是优势期，到了季后赛成了输分的时间段，这在前瞻里也写过——绝对是个隐患。与勇士汤追带队的衔接段交手，保罗竟然真的没占到便宜。勇士在这个阵容里，能给的错位点是韦斯特和尼克扬，第四节干脆连韦斯特都不用，继续用卢尼。保罗这场球大部分时间持球针对勇士内线打的都一般，没有他在常规赛虐遍勇士内线和侧翼弱点的风采，但是不是真的保罗后面比赛打卢尼也会这么费劲，可能还需要再看一场。保罗这场本可以尝试找一下尼克扬，让这个危险的三分手一直在场没有得到惩罚，火箭显然没有做到位。

保罗面对勇士五小阵容，持球能打的选择本来就有限，如果在衔接段还不能为火箭确立一点优势，那真的要累死哈登。火箭这场球稳定输出全靠哈登，保罗和戈登持球都没能打出效果，到最后的结果必然是哈登体力耗尽，火力续不上了。

火箭衔接段阵容防守槽点也不少，杰拉德-格林+安德森真的不要一起出场了，两个点防守都不好，勇士衔接段的传切就打出来了。另外，勇士那边已经基本是8人轮转了，火箭这边闲杂人等真的不能乱用了，该草首发就得草了。

火箭的小个阵容有隐患

火箭在第四节拿下卡佩拉，上五小阵容跟勇士搏命，最后还是没能挽回局面。因为今天落后的多，五小阵容具体打出什么效果可能不太重要了，但这套阵容是不是能对抗勇士，其实有点疑问。前瞻里写到，如果库里持球打不了卡佩拉，火箭就没必要撤下卡佩拉上五小——防守太矮，没护框。

哈登这个点太容易被过，火箭又提供不了护框

进攻端理论上的极致空间，比起卡佩拉在篮下牵制格林，未必效果更好，勇士锋线防守站位和预判太厉害，篮下协防和外线轮转可能真的可以兼顾。

格林放空塔克协防篮下，哈登分球，伊戈达拉预判出哈登的传球路线

如果说杜兰特是个火箭难以解决的问题，那么哈登同样是个勇士难以解决的问题，其实以哈登今天的得分产量、效率和助攻，杜兰特的输出都没能抵消哈登在进攻端的贡献。但火箭除此之外，其他人贡献太少。火箭在防守端也绝不是防不住杜兰特那么简单，固有顽疾没招，但一些可以想办法的，还是要努力解决。系列赛的G1就是个双方试探，试错的比赛，调整比抱怨阵容差距要更重要。想战胜卫冕冠军，可不是光靠一腔热血，输了一场就丧气，那期待了半个赛季的巅峰对决就有点令人失望了。

关注微信公众号：静易墨

微信号：jingyimo456

扫描二维码关注静易墨~~

来源：知乎 www.zhihu.com
作者：静易墨

【知乎日报】千万用户的选择，做朋友圈里的新鲜事分享大牛。点击下载

订阅：博文 (Atom)