

《总法律顾问手记——律政职场胜经》作者,任跨国公司总法律顾问多年。四川大学法学院法律硕士、中欧国际工商学院EMBA。原创作品,转载请联系作者获得事前授权。
2017年11月在全国地方法律顾问论坛杭州峰会上,我受邀做了主题发言,内容主要围绕着企业法律顾问在海外并购中及整合管理中需要注意的几个问题。其中探讨了中国跨国经营企业是否该向海外派驻自己的法务人员的一些看法,引起了现场听众的共鸣,希望我后续能够写文章做深入的探讨。
2018年4月16日中兴通讯案件一夜之间在媒体发酵,关于其违法证据被北美地区总部的法律顾问出卖的传闻说的有鼻子有眼,这也促使中国其他跨国经营企业管理者重新考虑:(一)是否将主要子公司的法务法规岗定为核心岗;(二)在核心岗位上是否有必要从中国派驻海外法务人员;(三)如果派驻,该采用何种模式?
本文围绕上述问题展开,既是对《总法律顾问手记#60┃中国企业海外并购后如何构建海外法务管理体系》的延伸;也是对读者要求和国际新形势的一个回应,希望能给中国跨国经营企业的法务管理者和CEO一些启发。
(一)中国跨国经营企业海外发展模式对人员派驻决定的影响
中国企业海外发展模式,在不少学者和媒体的表述中总结成三个模式:贸易式、契约式、投资式。个人并不赞成这种过于学术的分类。要讨论中国跨国经营企业的海外发展模式,先需要确定中国跨国经营企业的定义。我认为,企业的本质具有逐利性,也具有一定的属人性;从控制权及全球资源配置的角度来考察,比较符合中国跨国经营企业的实际。
跨国公司(Multinational Corporation,MNC),根据维基百科的定义,是在多个国家有业务、通常规模很大的公司。这些公司在不同的国家或地区设有办事处、工厂或分子公司,通常还有一个总部用来协调全球的管理工作。本文所说的中国跨国经营企业,我们不妨理解为总部或者控制权和中国有密切关系的跨国公司;无论是其总部设置在中国或者控制权在中国公民、法人手中。
我的拙见是,凡是称得上中国跨国经营企业的实体必须满足三个条件:首先它在世界主要市场有经营场所;其次有一个全球总部对生产、营销、配送、物流、供应、研发及人力资源网络等资源进行全球配置,以期达到协同效应,从而达到成本最优化、利润最大化;再次,总部设置在中国,或者其控制权在中国公民、法人手中。通过进出口贸易在海外经营是货物输出阶段;通过契约式在海外发展的企业处于服务和管理经验输出阶段;而本文所指的中国跨国公司是通过获得控制权,从而实现全球资源配置,追求利润最大化的企业,是资本输出的结果。
目前中国的企业在跨国经营中做得比较引人注目的,如海尔、华为、中兴通讯、联想、吉利汽车以及国家石油公司诸如中石化、中海油和中石油。但深究其海外发展模式,一种以通过并购为主的方式来实现全球扩张,如吉利、联想;也有主要通过伴随着业务扩张而设立自己的海外分子公司形式从而在海外站稳脚跟的本土企业,如华为、中兴通讯;当然,走花式混合的也不在少数。
选择某种海外发展模式,受国家政策、市场发展需要、企业文化、进入时间等影响,并无优劣之分。但进入海外市场的方式不同,决定了各企业扩张的商业模式上存在显而易见的差异,最终这会影响到企业在当地分子公司的实际控制力,进而影响管理层在某国是否派遣人员的决定。
(二)中国跨国经营企业对法务合规岗位的重新定位之需
无论选择并购或设立独立的分子公司的形式进入海外市场,人事任免安排是必须考虑的问题。
习惯做法是由母公司派高管到海外分子公司。即便是在收购兼并方式进行全球化经营的中国企业,无论全资收购也好、控股收购也罢,更无论是绝对股比的大股东、还是相对股比的大股东;一般会在并购交易快结束前确定相应的人事安排,包括董事会的人员任免安排,及其它核心岗位的人员任免安排。
对于CEO的人选和董事的人选,和西方人想象中的中国企业非自己人不用的观点不同,中国跨国经营企业多采取委托高端猎头全球搜寻人才的方式,我有幸观摩过其中的一小段落,过程相当国际化。当然如果是国有资本背景的中国跨国经营企业,注重政治性也是难免的,所选任CEO、董事人员多数是党组成员。但是,回到除CEO和董事人选之外的核心岗位的识别和人员任免安排上,中国跨国经营企业最关注财务人选,其次是传统的研发、制造、采购等岗位;坦率的说,在中国跨国经营企业中,能将法务与合规岗位识别为核心岗位的寥寥无几。
受中国商业文化和传统的影响,中国企业通常将人际关系置于组织机构关系之上,进而影响商业决策,导致中国的本土商业环境和文化,无法帮助中国企业培植出合法合规基因。缺乏透明性和主动内部监管机制;无法将合法合规经营放到战略高度去考虑,和西方大的跨国公司相比,不重视法律人员、合规人员的作用是中国跨国经营企业的常态。不可否认,在某些走出去企业中依然存在着高度政治化,这些是中国企业跨国经营过程中经常被诟病的点。
西方发达国家对合法合规的高要求,相应地对中国跨国企业的经营管理提出了新要求,首当其冲地将公司内部法务部和合规部门的建设提到了战略性高度。西方文化侧重管理层与员工之间的团队及合作、详细可行的长期计划、运作透明度及监管、多元文化融合、对腐败问题的严肃惩戒以及企业内互相关系的制度化。加上西方国家的法治传统深入人心,依然靠跑关系这一套方式去解决冲突和问题基本无效;因此内部法务和合规的重要性在中国跨国公司的海外经营中被凸显出来。最近发生的中兴通讯被美国政府制裁的案件,从另外一个角度说明了上述观点。
务实的跨国经营的中国企业会努力去适应当地的环境,重视法律对商业经营的重大影响,进而重新界定法务和合规岗位人员在跨国经营企业中的作用,将其定位为核心岗位人员。反过来,积极适应海外法治经营环境的中国跨国企业也会从从中受益,促使其在中国的母公司更规范的运营。
譬如在吉利汽车收购瑞典沃尔沃汽车的交易中,母公司吉利汽车得到的不仅仅是众所周知的技术、股权和知识产权。瑞典沃尔沃汽车的董事会下设审计委员会、采购委员会、薪酬福利委员会,不仅这些机制最后被母公司吉利汽车吸收引进,而且吉利汽车更进一步,在董事会下设了合规委员会。这一举措毫无疑问将有效的促进母公司吉利汽车在公司治理架构上的现代化进程,缩小和西方跨国公司之间存在的差距,从而在经营管理中越走越稳健,成为实质意义上的跨国企业。
(三)海外子公司关键岗聘用模式探讨
跨国公司的海外派驻,原则上只针对核心岗位人员和本地稀缺人员。当法务部、合规机构在中国跨国经营公司中的定位被调整到核心岗位时,那么从人力资源管理的角度,就会涉及到是否在世界各地的法务核心岗位的派驻问题。
在做出海外分子公司法务合规人员派驻决策之前,法务管理者有必要先从成本的角度来考察下海外派驻人员的三种模式:海外派驻(expatriate)、当地聘用(local hire)、出差(commuter) 。 在展开讨论之前,我先用表一来对这三种聘用模式的优劣从不同的维度做简要的分析,使读者能更充分的理解这三种模式之间的差异。
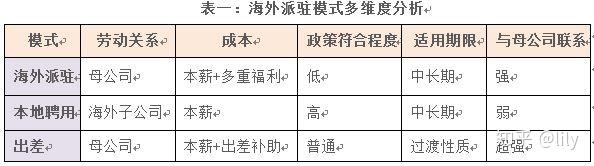
海外派驻的方式下,劳动关系保持和原公司不变,但公司会为员工办理当地工作签证,也会在薪资以外提供包括生活津贴、眷属津贴、探亲假与探亲机票、搬迁补助等福利。好处是有利于母公司企业文化的输出,公司高层对派驻的人员有可靠的信任度,方便沟通协调;劣势是人事费用非常惊人,正规的跨国公司为此付出的代价将包括:本薪+生活津贴+社会保险+搬迁补助+住房津贴+眷属福利+探亲假/探亲机票+税负补贴/汇率补贴等,这些数字加在一起对公司而言,是巨大的负担。基于以上原因,跨国公司近年都在进行"本地化"调整,也就是将海外派驻人员的外派身份取消,让员工变成本地聘用的身份。
本地聘用,在东道国招聘符合公司对人员资质要求的员工,无论员工是本国人还是外籍人员,聘任条件等同于当地员工。公司可能会提供一笔搬迁补助,取决于双方谈判结果,但没有任何外派人员福利;劳动关系上员工身份是本地员工,如果员工是非本地籍,公司会协助员工办理签证事宜,但员工要对此负主要责任。本地聘用模式的好处是,在海外市场聘用合格人才与东道国所推动的劳工政策不谋而合,政治法律风险小;且费用相较于海外派驻大幅度减少,有时候海外派驻的福利产生的费用就有可能比员工的本薪还要高。劣势是员工和母公司不存在聘用关系,磨合期相对长,信任度相对低,招聘失败的概率比较高。这些劣势也导致有的跨国公司会采取变通方式。譬如要求母员工先解除合同,再和海外子公司签订劳动合同;但在这种情况下,存在母公司的资深核心员工并不愿意接受此类工作机会的问题。
出差,公司以出差方式派遣员工去另外一个国家短期工作,通常会依照出差日期提供给员工差旅费。这种模式通常用在项目支持上比较多,多为短期技术支持和服务;且这种模式常作为未来长期海外派驻的过渡模式,以帮助拟长期海外派驻员工提早了解未来的生活工作场景,有一个文化和职业的缓冲期。好处是比较灵活,在项目前景或当地市场前景不明时,可作为一种过渡模式操作;由于劳动关系保持不变,员工相对而言也乐于做这种尝试,最终再根据项目或市场的前景做出是否接受海外派驻的决定。劣势是员工每月频繁往返,机票住宿成本比本地聘用高;另一个方面,由于员工有大量的时间在两地奔波,许多时候是在出差途中,员工有效工作时间大大降低,从而降低劳动生产率;另外,对员工的管理控制力可能会面临一个真空区,由于东道国没有法律上的管理权,母国又由于时差和距离问题的存在,实施有效的人力资源管理的难度比较大。
(四)决定派驻与否的几个关键因素
第一,派驻法务和合规人员与否,和商业发展模式息息相关。
如果是并购方式进入的,需要考虑并购后整合的问题,直接派法务驻扎海外是否合适就会是个很慎重的决定,尤其是当被并购的公司在业内本身就是比较成熟的公司,已经有成熟的法务部的情况下。如果是自我扩张的方式进入当地市场的,那么派驻条件合格的中国人当地开展工作,在公司政治这个层面的障碍就小得多。因此我们有必要在做出相关决定前,将商业发展模式这个关键因素考虑在内。
拿华为为例,其发展模式主要是从一个个海外市场的项目做起,通过自我扩张模式进入海外市场。相应的,华为的商业发展模式决定了它对海外子公司有绝对的主导权,它可以根据主要市场的区分,在各大洲设立了地区总法律顾问,由中国人担任;同时在当地每个国家派驻中国籍海外法务管理人员;在汇报线上,地区的总法律顾问向集团法务部汇报。可以说,这种以海外派驻母国法务为主开展工作的模式,与华为的海外事业商业发展模式不无关系。
第二,以海外并购模式进入东道国市场的中国跨国经营企业,派驻法务与合规人员与否,应考虑母公司与海外子公司的管理实力。
中国大型企业在国家信贷强力支持的背景下,走出去的不在少数。但论管理能力和管理实力,许多被并购对象反而高于母公司。举例来说,在吉利汽车收购沃尔沃汽车的案例中,瑞典沃尔沃汽车虽然是被收购公司,但其公司治理架构按照美国上市公司治理架构设置,非常完善成熟,其法务部也是管理成熟的。相比之下,吉利汽车虽然是100%的股东的,但其当时的法务部相比海外发达国家有很大差距;因此在这个阶段,即便是瑞典沃尔沃汽车公司的General Counsel岗位是核心岗位,吉利汽车并不适合派遣法务管理者接管,否则引起文化上和管理上的不认同不说,基本无法开展工作。
遇到上述情形,睿智而有全球化格局的中国跨国经营企业总部管理者,则会主动的掘弃关键岗位上非自己人不用的政治为主导用人方针,而以企业的正常运营和盈利有效增长为出发点做决策。
实际上,吉利汽车在瑞典沃尔沃汽车的财务岗位上曾派遣过副CFO,但是一年后不得不铩羽而归。主要原因在于中国严重缺乏国际化人才。中国籍国际化人才和瑞典这样的成熟国家可获得的人才相比,有不小的差距。即便是财务类最核心岗位,当被并购公司的成熟度高于母公司时,这种海外派驻很难有效;法务合规领域亦复如是。考虑到人员派驻方式效果不理想,一年后吉利在瑞典沃尔沃汽车高级管理人才和核心岗位的人员任用上,改变为自治管理方式。因为省略了文化磨合和管理震荡,最后反而取得了理想的效果,瑞典沃尔沃汽车很快开始盈利。
第三,考虑是否需要派驻海外法务合规人员要参考当地子公司的发展阶段,尤其是人员规模和净利润这两个指标。
仅仅考虑海外扩张模式、子母公司的实力博弈是不够的,母公司法务管理者和人力资源管理者需同时判断海外业务的发展阶段,然后做出是否应该派驻的决定。
如果海外业务刚刚起步,即使是通过自我扩张方式进入的主要海外市场,可请母公司有资质的法务在总部兼任。同时,海外业务的发展阶段和人员聘用成本又是有机的联系在一起的。
以我的经验,在当地子公司净值利润超过500万美金,并且当地员工人数超过50人时,总部法务管理者考虑聘请一位专职内部律师才是合理的。在未达到这两个指标的情况下,总部的法务管理者可以请当地外聘律师协助解决海外子公司经营过程中发生的法律问题,或考虑母公司有资格的内部律师在母国兼任。
第四,决定派遣海外子公司的法务及合规人员时,除非需要雇佣的人才仅在母公司存在,否则应该优先考虑本地雇佣的模式。
作为法务管理者,成本是在国际招聘时需考虑的关键性因素之一。鉴于海外派驻模式成本昂贵,同时成熟的西方主要市场人才供给充足,即便是在本地雇佣中国籍的人才,也是不难实现的,因此应重点考虑本地聘用的模式。除却成本因素,派驻人员在海外开展工作的难度也是一个考虑因素。譬如前文所举例被并购企业本身具有成熟的管理机制和管理人员时,非要派驻中国的来自母公司的员工,在工作中被排斥和轻视时有发生,文化融合和职业融合的难度可想而知,反而不利于开展工作。
如果总部对海外子公司关键岗位人员缺乏基本信任,可以考虑本地聘用。这样的好处是一则可以如愿替换成中国总部期待的"自己人",另外本地聘用成本上和本地员工相当,语言上文化上没有太大差异,容易在工作中被本地员工所接受。
第五,没有绝对自己人,信任是逐步建立的,不应在选任上存明显偏向。
中国跨国公司的海外经营,需要的是从国际化、多元化的人才身上求同存异,互相学习进步,增强互信和内部透明度,逐步向建立健全、先进的公司治理机制发展;而不是靠自己人把控法务合规等关键岗位,利用信息不对称从事违法经营事项。
毕竟大部分和中国关系正常的西方国家给予包括中国的外国企业以国民待遇。国民待遇包括享受东道国给予的政策优惠,也包括受当地法律监管接受违法惩戒。如果中国跨国公司在海外存在违法经营行为,并不会因为你是总部在外国的跨国公司,而网开一面而给予原谅和理解的。
另外,西方国家讲究权利平等;如果在员工选任上存在明显偏向,很有可能会被告,这方面问题在中国较少发生;而国外有强大的工作撑腰,中国跨国经营企业需要在包括人员选任等方面及时调整思维模式。
(五)总 结
现在中国企业从事海外经营的越来越多,许多企业正在逐步成长为中国跨国经营企业的过程中。笔者经常被大公司法务问,公司提出要派我去海外市场,我该不该接受的问题。
法务和合规人员被公司委任派驻海外,反映了中国跨国经营企业的法治经营意识的提升;但我们也该看到,仍然有不少走出去企业并没有将海外的法务和合规岗视为关键岗位,在派驻上依然是以财务为主。这一点,有待中国跨国经营企业管理者的意识逐步提升。
对被委派的中方企业人员而言,这是难得的机会;但作为法务管理者,我们要考虑的不仅仅是派自己人是否更安全可靠的问题。相反,企业发展模式和发展阶段的对比、候选人资质和本地雇佣人员资质的对比、子公司和母公司实力的对比,比海外法务合规岗是否是中国人,更为关键。
法务管理者的出发点应围绕着派驻的决定是否对企业在当地的经营发展更为有利这个总体方针来考虑;同时,新的商业发展趋势,更促使跨国经营的中国公司法务管理者要具有前瞻眼光,在海外法务合规人员的任免上保持开放的态度,不拘一格降人才!
李熠
2018/5/18日夜于杭州
PS.欢迎您通过"在行"网及"在行"APP搜索"李熠Lily"进行法律职业发展一对一法律预约。想参加"律政职场先锋私董会"的,请关注公众号"律政职场先锋"的活动预告(电子邮箱:legalclass@126.com;微信:lilyforwork,注明姓名、单位)。
来源:知乎 www.zhihu.com
作者:
lily 【知乎日报】千万用户的选择,做朋友圈里的新鲜事分享大牛。
点击下载

行进的间断(
为线性退化场)
通过单个跳跃间断连续,且满足:
,且有m-1个独立的首次积分
其中,A是一个常系数(矩阵)。
,等于体积微元与外界交换的流的变化
。
,这就叫做Riemann问题。
,
处解不连续,作特征线,特征线上解断了,如图,特征线左右值恒为ul,ur
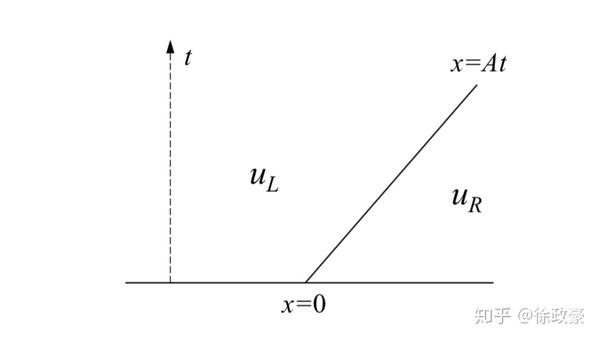
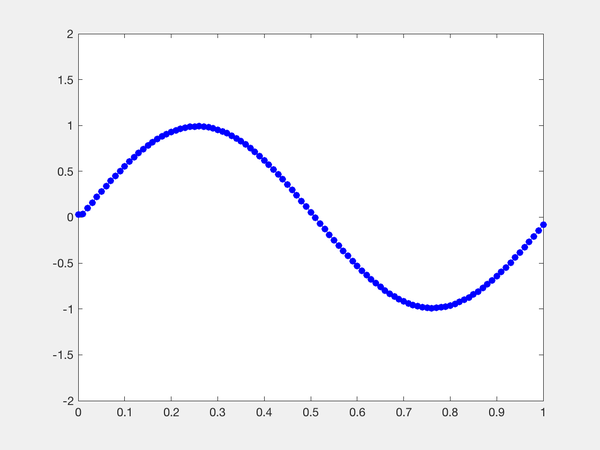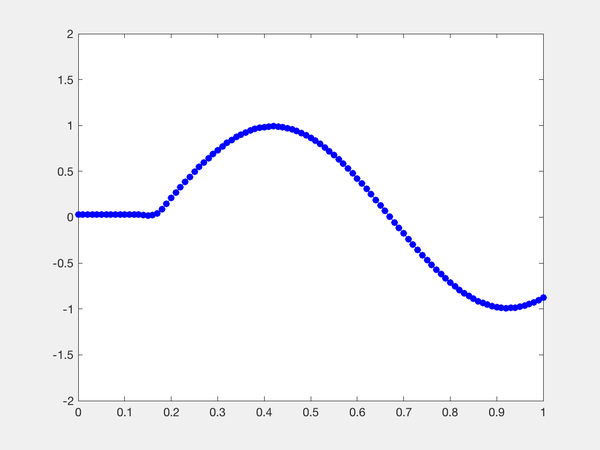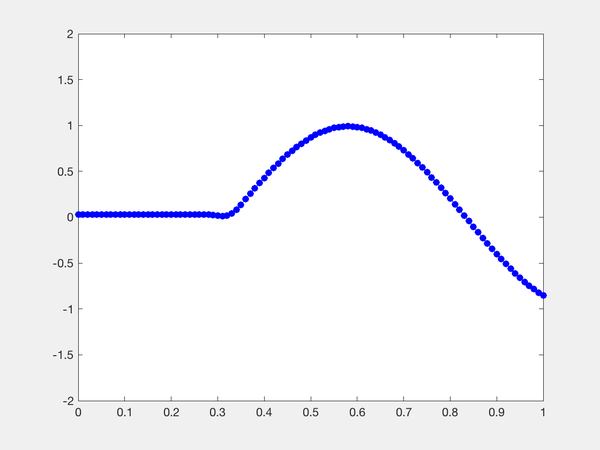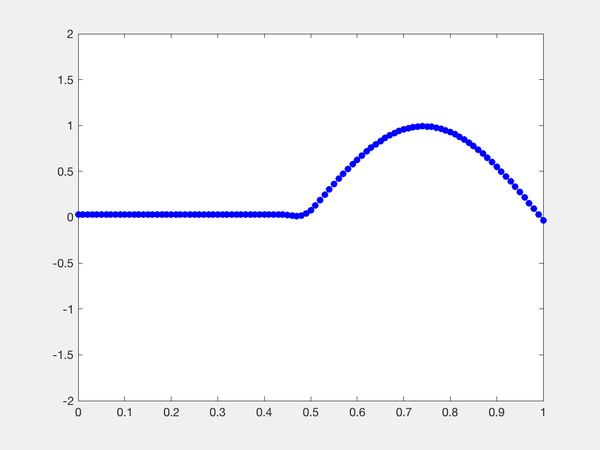
其中,A是一个常系数(矩阵)。
在
曲线上是常数,所以当然可以积分,得到从
出发的特征线为:
,
是一个标量,那么只要解还是光滑的,特征线一定都是射线。
,但是呢,如果
,特征线就会相交,但是物理量不可能相互穿过而无影响(保持光滑),另一方面,如果
,特征线会发散。我们具体来看
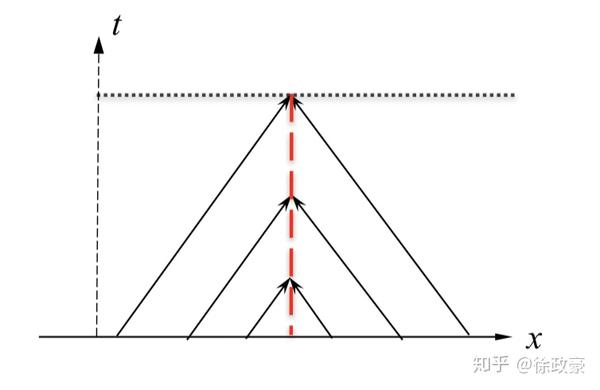
,特征线相交与射线:
,在这里形成一个激波。
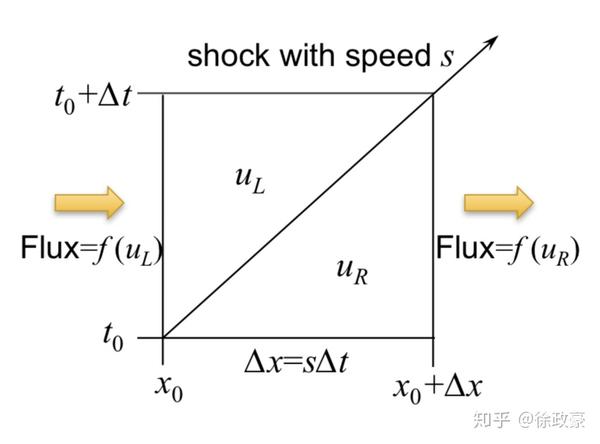
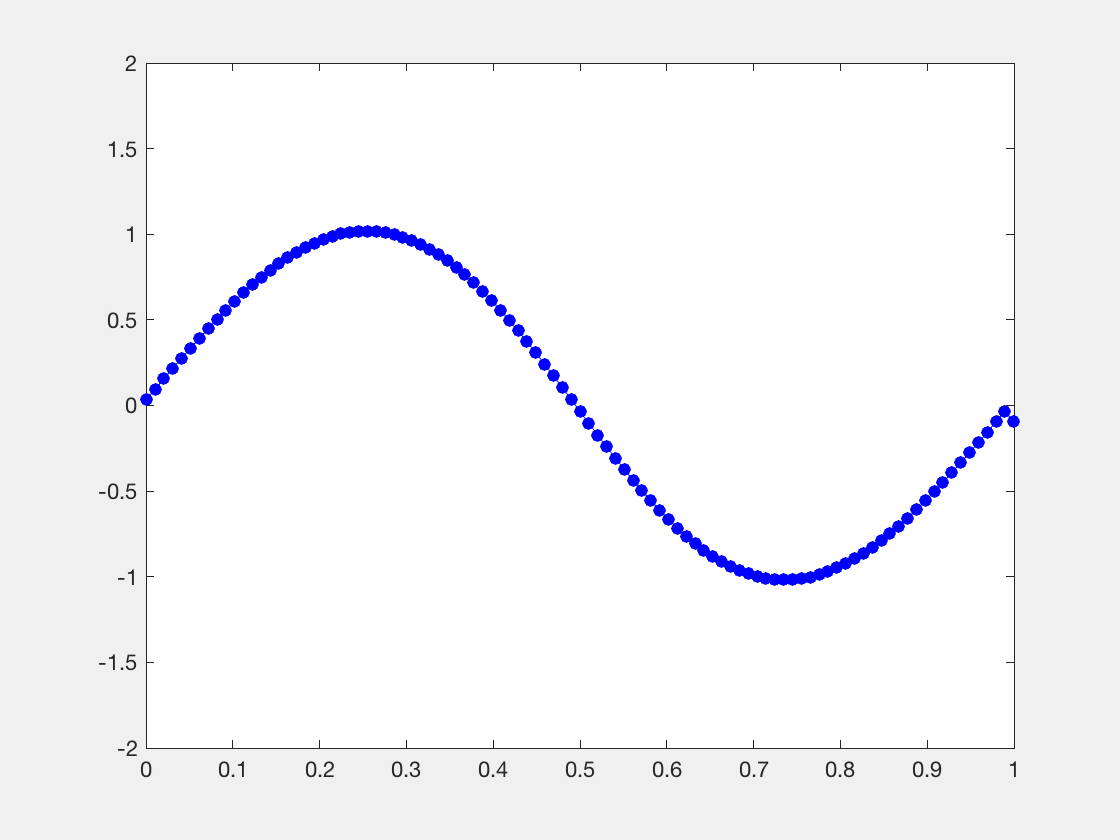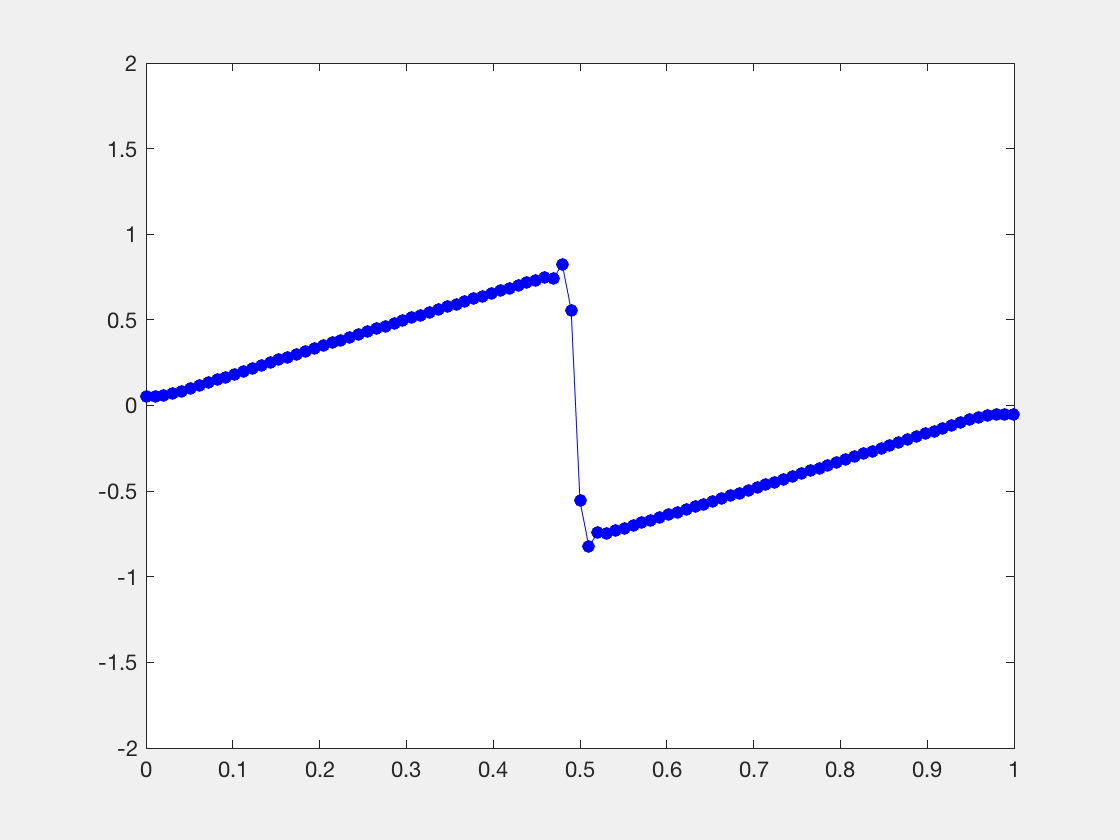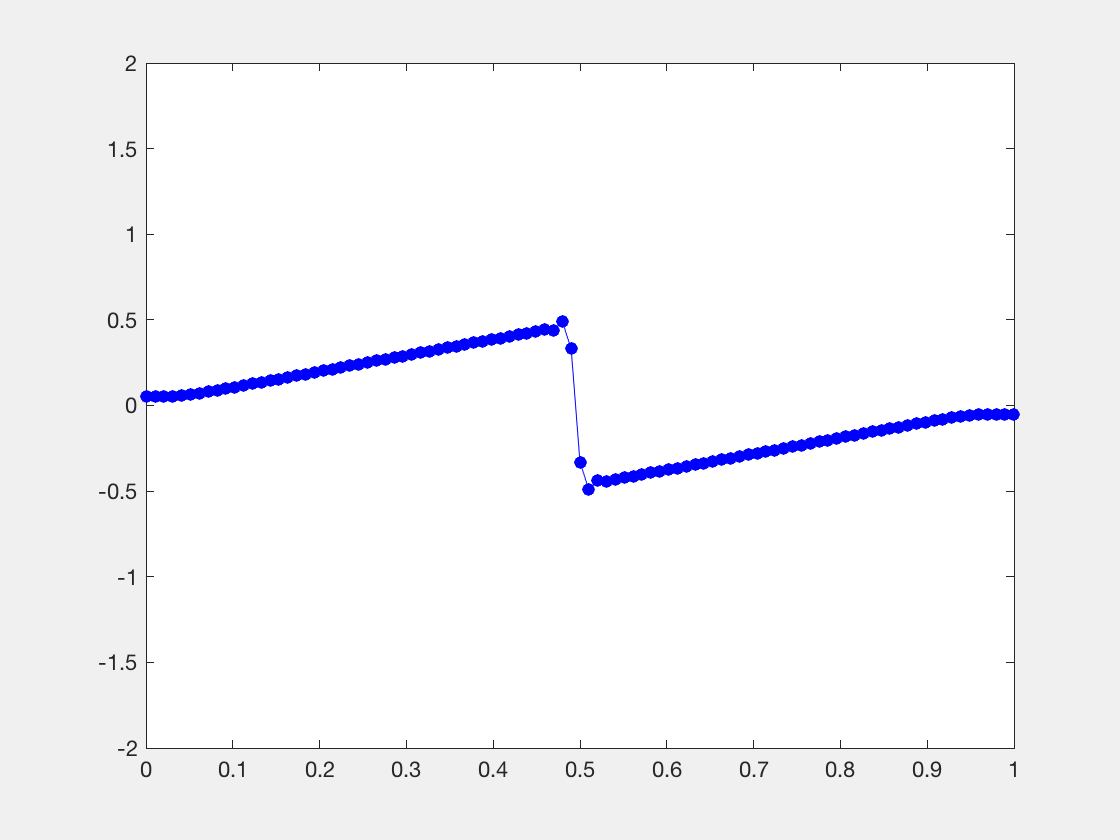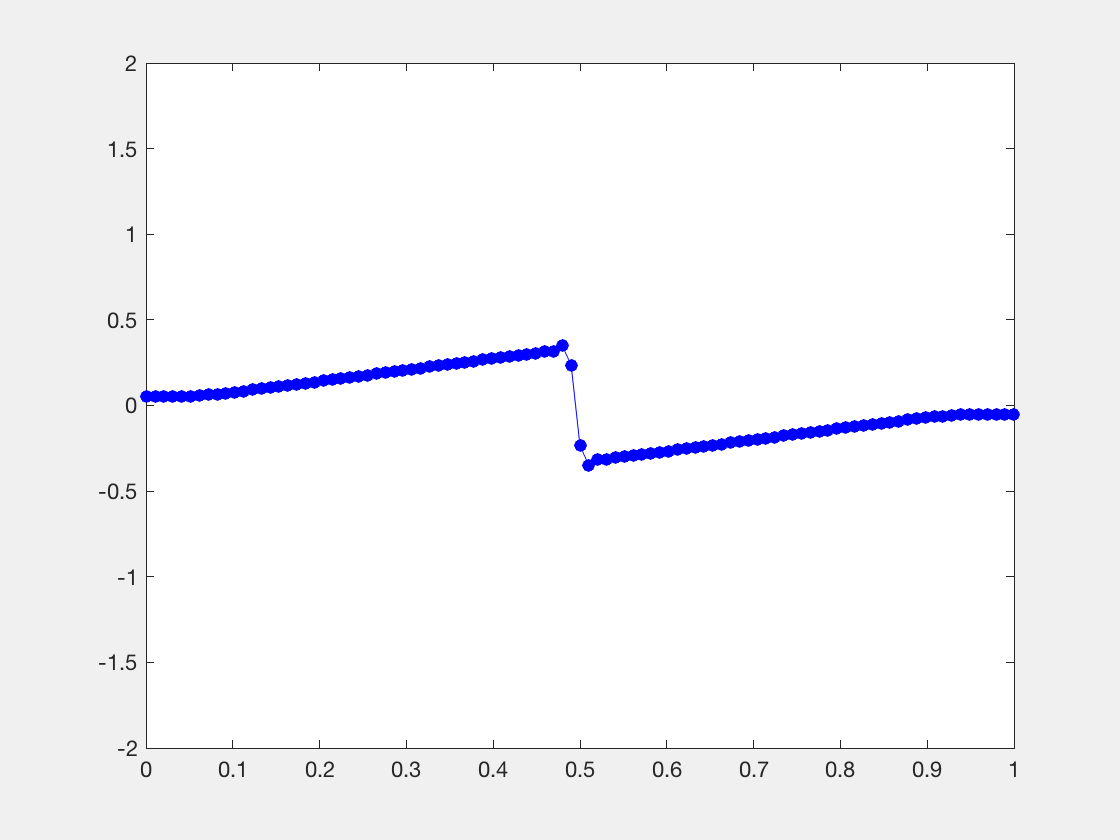
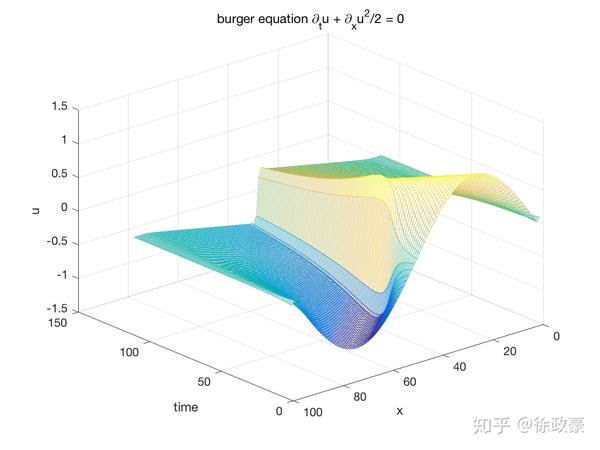
,对于黎曼问题
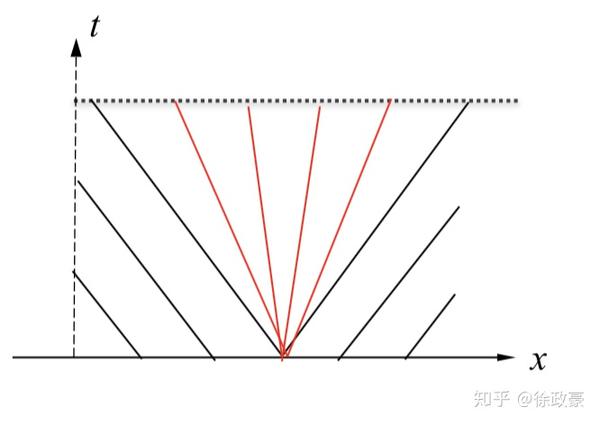
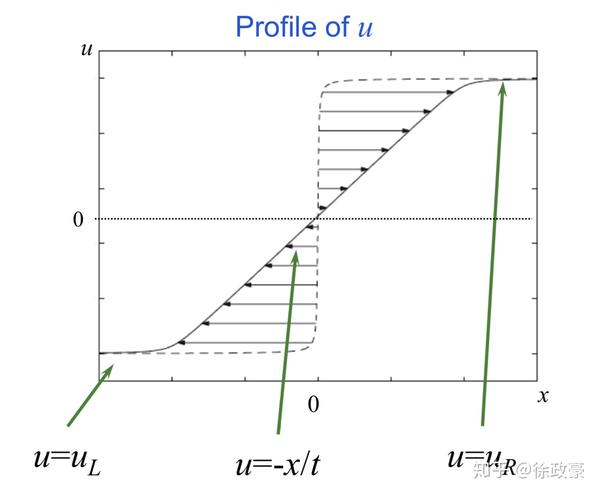
,其中
是任意的,
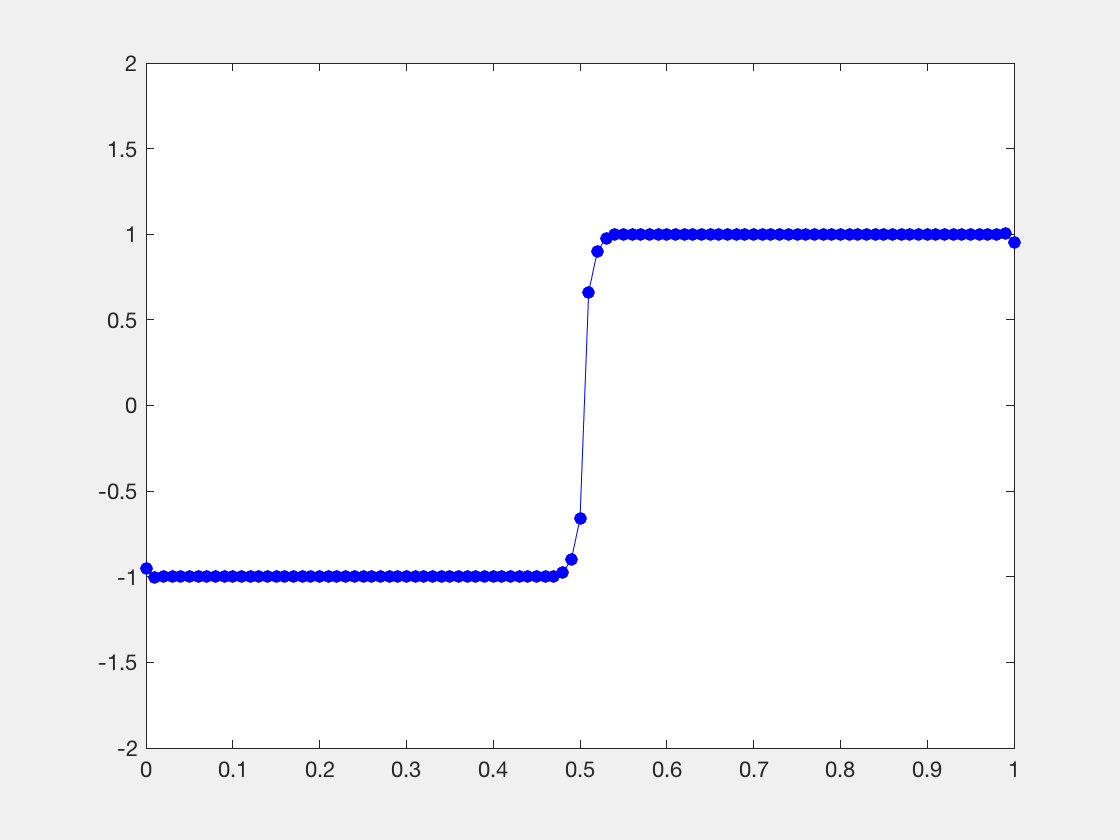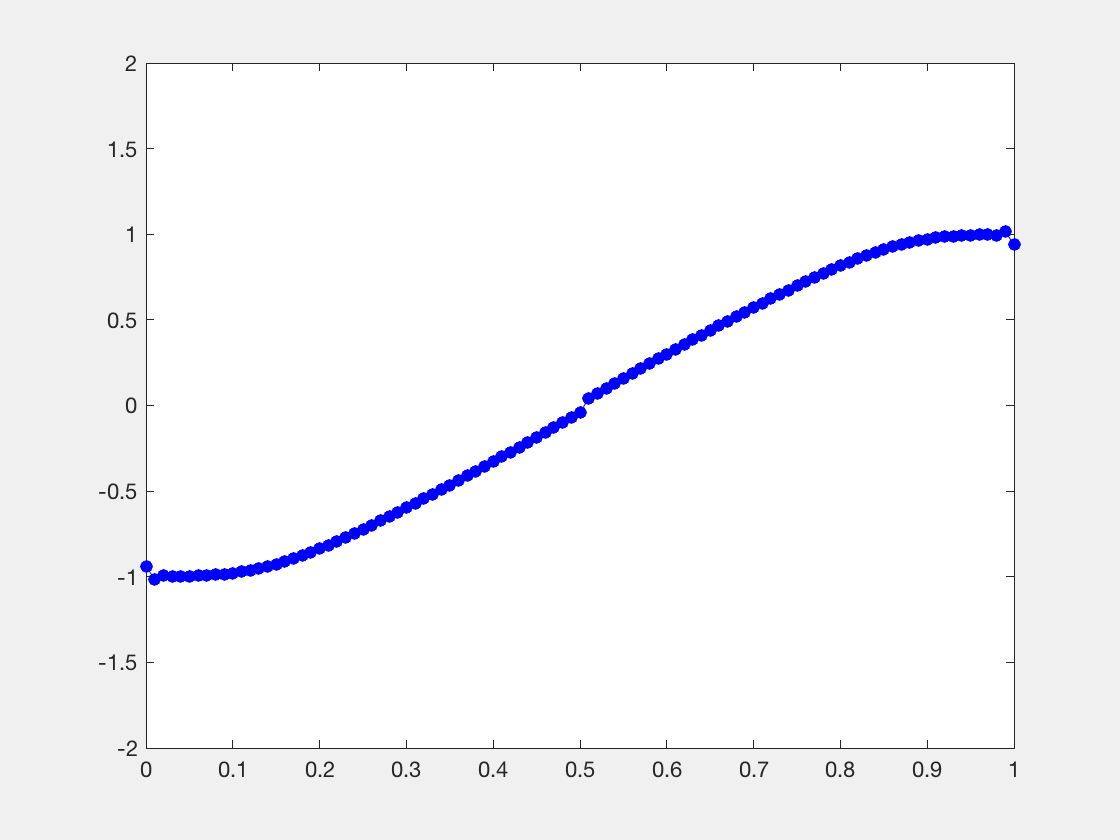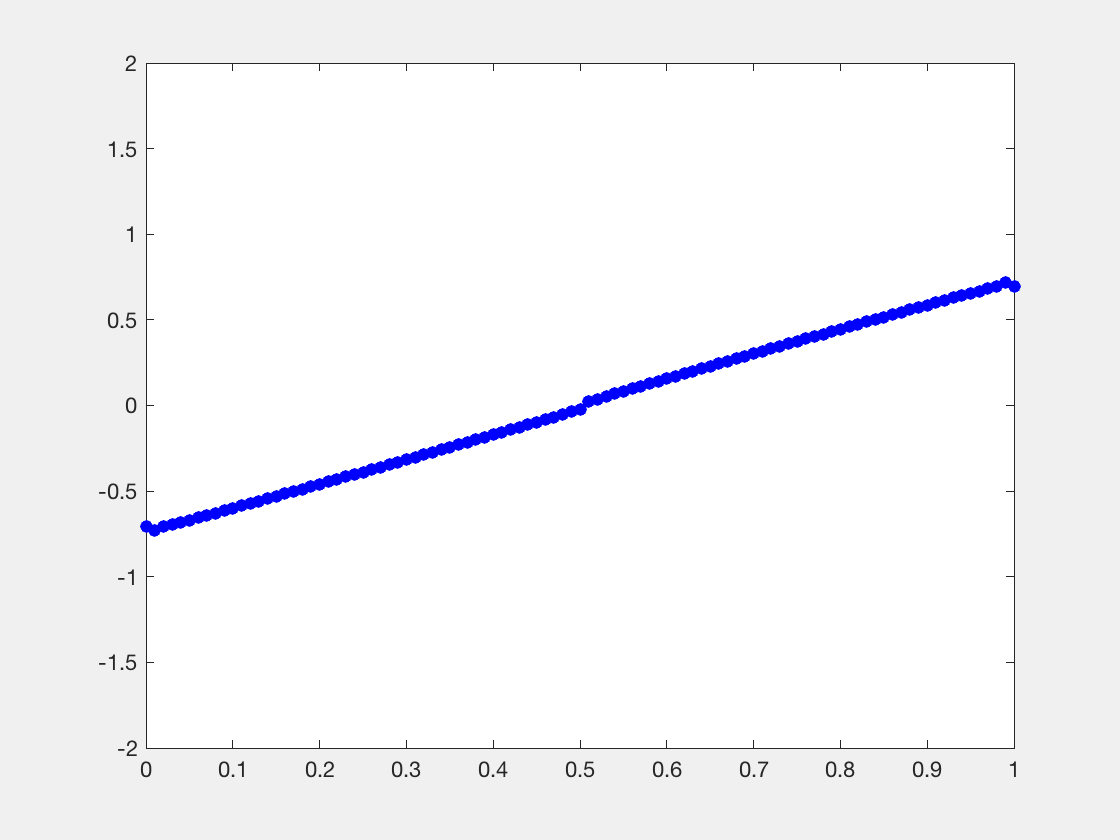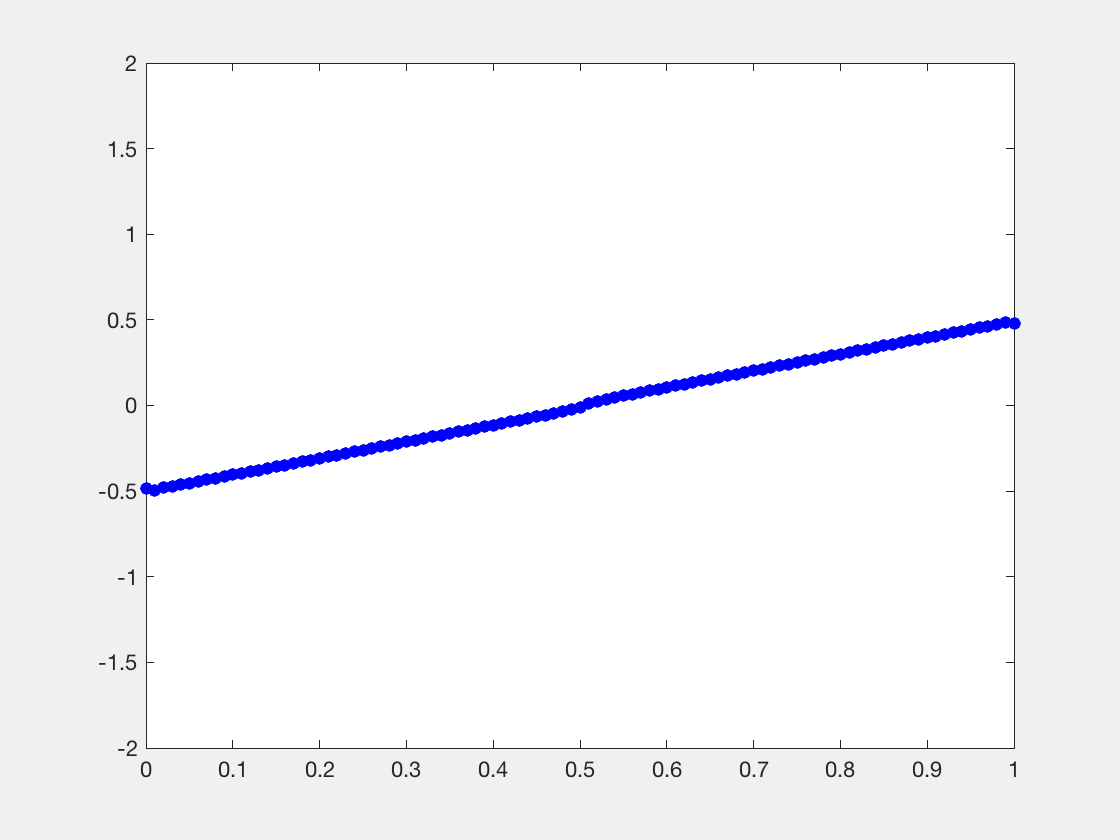
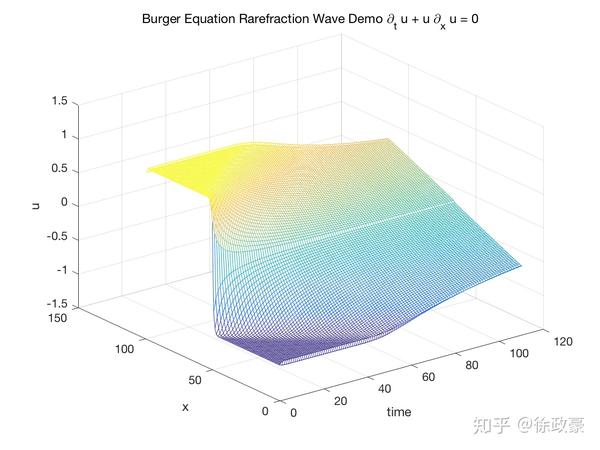
处的Riemann问题会产生解的非光滑性。而非光滑的地方,拟线性PDE则失效了。
上
成立,而是要对任意控制体都成立,大家明白意思就好)
被称为弱解。
变为无穷大,爆破发生在由
发散出来的特征线
,其中 x0满足:
,且
是最大值的点
上, 令
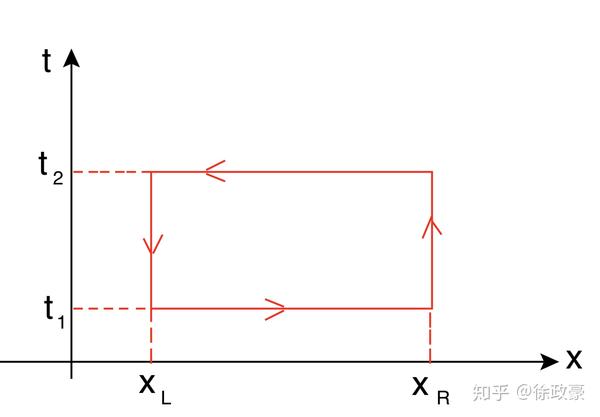
是下面四条曲线构成的闭回路,即在间断线的任意的一点
附近取小邻域:
拆成四条曲线,分别计算积分,得到:
中
因为t是固定的,所以这一项是0
是任意的,所以在间断线
上,
是间断速度,
和一个对应
的特征场的速度为
的间断或波,则跨越间断线的RH条件:

,特征值
的1-波的RH条件为:


