经典网文分享

这次来简单的看一下整数量子霍尔效应吧
~~(｡•ˇ‸ˇ•｡)~~

1897年发现的经典霍尔效应我们已经非常熟悉了，如图，霍尔电压 $U_{H}$ 和磁感应强度 $B$ 成正比。

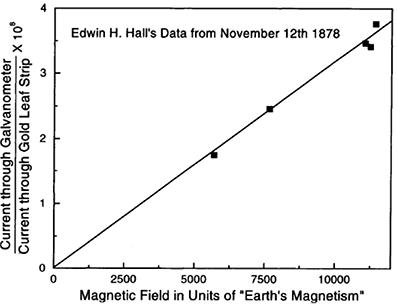
这次我们来看一看整数量子霍尔效应，第一部分介绍整数量子霍尔效应的实验结果，第二部分和第三部分对整数量子霍尔效应做理论上的解释。当然，这里的解释主要是建立在单电子图像上的。

不过呀，下面我们就会看到，单电子图像只能解释霍尔电阻 $R_{H}$ 为什么会产生平台，但解释不了横向电阻为什么会变成零。

第一部分：实验结果

在整数量子霍尔效应中，电子被约束在二维平面上运动（二维电子气）。那么，我们到底怎样才能获得二维电子气呢？我们可以用电场使电子局限在半导体表面，这里可以采用硅金属氧化物场效应管来实现。实验在低温和强磁场条件下进行（电子完全极化）。

为了更方便的做进一步讨论这里给出有关霍尔电阻与纵向电阻的两个表达式：

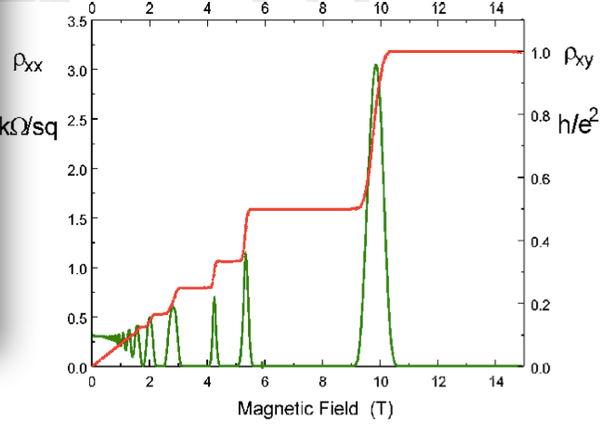
$R_{H}=\frac{U_{H} }{I}=\frac{E_{y} L_{y} }{j_{x} L_{y} } =\frac{E_{y} }{j_{x} }= \rho _{xy}= \rho _{H}$ ； $R_{x}= \frac{U_{x} }{I}= \frac{E_{x} L_{x} }{j_{x} L_{y} } =\rho _{xx} \frac{L_{x} }{L_{y} }$ ，

实验结果如图，它和我们熟知的经典量子霍尔效应有很大的不同。

1，如图中红线：这里的 $\rho _{H}$ 和 $B$ 不再呈线性关系，二维电子气的Hall电阻 $R_{H}$ 与 $B$ 的关系是在总的线性趋势上出现一系列的平台（称为量子化的Hall电阻），它们出现在 $R_{H}=\frac{h}{ie^{2} }$ ，（ $i=1,2,3,4,......$ ）

2，量子Hall电阻 $R_{H}=\frac{h}{ie^{2} }$ 的值与具体材料无关，仅仅依赖与常数 $h$ 和 $e$ 。

3，如图中绿线：对应平台的 $B$ 值处，纵向电阻为零。

下面，我们用单电子图像对整数量子霍尔效应做一个解释。但是，单电子图像是无法解释"3"的。要想解释"3"的话我们必须要考虑到电子之间相互作用形成的强关联集体态。

第二部分：量子Hall电阻

这部分来解释一下，为什么 $R_{H}=\frac{h}{ie^{2} }$ ，以及为什么会出现平台。

1，朗道能级：

带电粒子在均匀磁场中的运动问题早在1930年就被朗道解决了。考虑沿z方向的均匀磁场 $B$ ，选取磁矢势为： $A=(-B_{y},0,0 )$ ，则能量本征方程为：

$\frac{1}{2m}\left[ \left( \tilde{p_{x} } +\frac{eB}{c}y \right) ^{2}+\tilde{p_{y} }^{2} + \tilde{p_{z} } ^{2} \right] \psi -\mu s_{z}B\psi =E\psi$ ，其中 $-\mu s_{z}B$ 是电子自旋磁矩在磁场 $B$ 中的能量。由于Hamilton量中不含坐标 $x$ 和 $z$ ，因此 $p_{x}$ 和 $p_{z}$ 都是常数，我们可以将 $\psi$ 写为：

$\psi (x,y,z)=exp\left[ i /\bar{h} (p_{x}x+ p_{z}z ) \right]\chi (y)$ ，（文章里 $\bar{h}$ 代表约化普朗克常数）

将上式代回到能量本征方程中去可以发现， $\chi (y)$ 满足如下方程：

$\chi ''(y)+ 2m/\bar{h} ^{2} \left[ \left( E+\mu s_{z} B-\frac{p_{z}^{2} }{2m} \right) -\frac{1}{2}m\omega _{c}^{2}(y-y_{0} )^{2} \right] \chi (y)=0$ ，

其中： $y_{0}=-\frac{cp_{x} }{eB}$ ， $\omega _{e}=\frac{eB}{mc}$ ，可以发现，上式正是一维谐振子所满足的方程，容易解得：

$E_{n}=\left( n+\frac{1}{2} \right) \bar{h} \omega _{c} +\frac{p_{z}^{2} }{2m}-\mu s_{z}B$ ，相应的本征函数为：

$\chi _{n}(y)=\frac{1}{\pi ^{1/4}a^{1/2}\sqrt{2^{n}n! } } exp\left[ -\frac{(y-y_{0} )^{2} }{2a^{2} } \right] H_{n}\left( \frac{y-y_{0} }{a} \right)$ ，

上面写了这么多，说白了就是解了一个定态薛定谔方程，下面我们来观察一下方程的解：

可以发现， $p_{x}$ 并不进入能量表达式，但它通过 $y_{0}=-\frac{cp_{x} }{eB}$ 确定谐振子的平衡位置。也就是说它影响着能级的简并度。

若粒子x方向运动不受限制，那么 $p_{x}$ 可以取任意值，能级是无穷度简并的。若电子被局限在面积为 $S=L_{x} L_{y}$ 中运动，考虑x方向的范围限制在 $L_{x}$ 内，那么 $p_{x}$ 的值就是分立的，即： $p_{x}=\frac{2\pi \bar{h} }{L_{x} } l$ ， $l=0,\pm 1,\pm 2,\pm 3,......$

在 $L_{y}$ 长度内能容纳下的平衡位置数为： $\frac{L_{y} }{\Delta y_{0} }=\frac{eBL_{x} L_{y} }{hc}$ ，由此可见：

单位面积的平衡位置数目即能级的简并度为： $n_{B}=\frac{eB}{hc}$

面积为 $S=L_{x} L_{y}$ 时平衡位置数目即能级的简并度为： $N_{B} =S\cdot n_{B}=S\frac{eB}{hc}$

2，量子Hall电阻：

在整数量子霍尔效应中，电子被局限在二维 $x-y$ 平面内运动，没有 $z$ 方向的自由度，且强磁场下电子被完全极化，此时，能量的本征值可以写为： $E_{n}=\left( n+\frac{1}{2} \right) \bar{h}\omega _{c}$ ，这就是朗道能级，我们上面已经讨论过它简并度的问题。下面我们用它来给出量子霍尔电阻 $R_{H}$ 的值。

样品上朗道能级的简并度为： $N_{B}=n_{B}L_{y} L_{x} =\frac{e}{hc}BL_{x} L_{y} =\frac{\Phi }{hc/e}$ ，容易发现，分母正是磁通量子 $\Phi _{0} =\frac{hc}{e}$ ，所以： $N_{B}=\frac{\Phi }{\Phi _{0} }$ ，通过这个关系式我们可以发现，如果一个朗道能级被填满，那么每个电子就可以"分摊"到一个磁通量子。若有 $i$ 个朗道能级被填满，则总电子数满足： $N=iN_{B}=i\frac{\Phi }{\Phi _{0} }$ 。

我们定义朗道能级的填充因子为： $\nu =\frac{n_{s} }{n_{B} } =\frac{n_{s} }{eB/hc}$ ，其中 $n_{s}$ 为电子密度。它是电子表面密度与朗道能级简并度的比，若 $\nu =i$ （整数），则有 $i$ 个朗道能级被完全填充。

当有 $i$ 个朗道能级被完全填充时，考虑到经典霍尔效应中的关系式： $R_{H}=\frac{B}{n_{s}ec }$ ，可得：

$R_{H}=\frac{B}{n_{s} ec} =\frac{h}{ie^{2} }$ ，我们在此给出了量子Hall电阻的值，它出现在朗道能级被完全填充的时候。

3，为什么会出现平台？

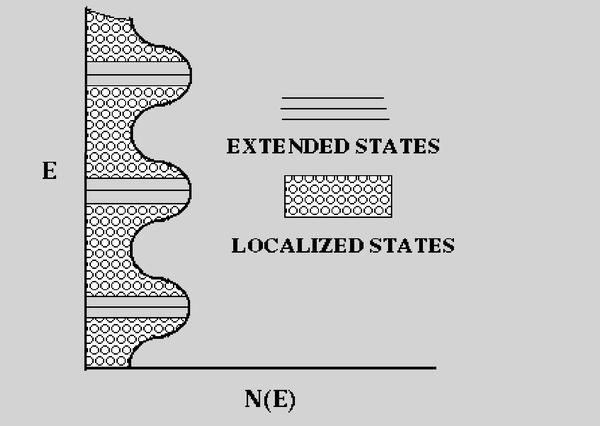
在整数量子霍尔效应中，朗道能级的简并度会被Hall电压与杂志势解除，朗道能级会展宽成为宽度有限的局域态，如图。

当一个朗道能级被填充满时，若此时磁场 $B$ 减小，根据上面的讨论，朗道能级所能容下的电子数就会减少，根据泡利不相容原理电子会"跑"到下一个朗道能级上去，这么看，电阻应该是连续变化的。但是，由于有局域态的存在，"多余"的电子会先"跑"到局域态上，它们不参与传导过程，因此并不导致Hall电阻的变化，这就是平台。

第三部分：量子Hall电阻的普遍性

1，量子Hall电阻是与材料本身无关的，1981年，Laughlin从规范不变性这个基本的物理学原理说明了这个问题，他对整数量子霍尔效应的诠释并没有依赖哈密顿量的具体形式。

考虑一个周长为 $L_{x}$ 的带状样品形成的闭合环，处处有垂直于带的均匀磁场 $B$ （沿 $z$ 轴方向），带的上下侧有电压降 $U_{H}$ （ $y$ 轴方向），沿带子的方向有电流 $I$ 流过（ $x$ 轴方向）。由于 $\rho _{xx} =0$ ，体系无耗散，能量守恒。容易得出： $I=c\frac{\partial E }{\partial \Phi }$ ，电子的波函数为：

$\psi (x,y)=exp\left( ip_{x}x/\bar{h} \right) \chi (y)$ ，波函数的单值性要求： $p_{x}=\frac{2\pi \bar{h} }{L_{x} }n$ ，

现在，假设磁通量变化一个磁通量子，基于规范不变性的要求，相应的波函数就需要乘上一个相因子 $exp\left[ i(2\pi x/L_{x} )\right]$ ，这相当于各个电子的 $p_{x}$ 都改变 $2\pi \bar{h}/L_{x}$ ，取代了前面一个电子原有的 $p_{x}$ 。

磁通量的变化会导致 $x$ 方向产生感应电场，电场导致 $y$ 方向的电荷运动，则，两端电势差为 $U_{H}$ ，设有 $i$ 个朗道能级被填满，则能量变化为： $\Delta E=ieU_{H}$ 。结合以上讨论可得：

$I=c\frac{\Delta E}{\Phi _{0} } =c\frac{ie}{\Phi _{0} } U_{H}=\frac{ie^{2} }{\Phi _{0} } U_{H}=\frac{ie^{2} }{h}U_{H}$ ，这正好给出了： $R_{H}=\frac{h}{ie^{2} }$ 。

2，注意到，我们以上所有的讨论都没有考虑周期场的问题，Thouless在Laughlin之后，考虑到了周期势场的问题，并且给出了Hall电导的拓扑意义。下面简单的给出一些结论，Thouless给出Hall电导为：

$\sigma _{xy}=\frac{e^{2} }{2\pi h} \oint_{}^{} <u_{\alpha } |\frac{\partial }{\partial k} |u_{a}>\cdot dk$ ，其中回路积分环绕磁Brillouin区边缘，它代环绕一周后相位的变化，考虑到波函数的单值性，它只能为 $2\pi i$ ，即给出： $\sigma _{xy}=\frac{ne^{2} }{h}$ 。

我们要求磁矢势满足周期性边界条件，其等价于把矩形样品"粘合"成环面，从这个角度看可以得到Hall电导的拓扑意义：考虑一个以Brillouin区为环面底流形的 $U(1)$ 丛，容易发现，Hall电导即为基态波函数在其上的第一陈类。

最后再说两句

在整数量子霍尔效应之后，1982年又发现了分数量子霍尔效应。

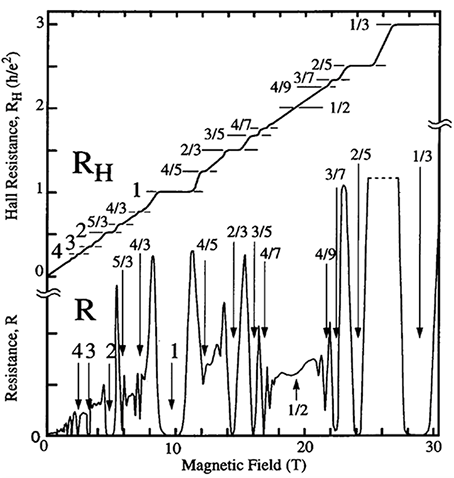
分数量子霍尔效应发现后不久，Laughlin很快就意识到，电子之间的相互作用十分重要，其导致强关联。他给出了描述这种体系的波函数，这就是著名的Laughlin波函数：

$\psi _{m} (z_{1},..., z_{n} )=\prod_{j<k}^{n}(z_{j}- z_{k} ) ^{m} exp\left\{ -\frac{1}{4}\sum_{l=1}^{n}{|z_{l} |^{2} } \right\}$ ，其中 $m$ 为奇数。

Laughlin当时借助液氦理论中的模型波函数，得到了Laughlin波函数。不过从二维分数统计的角度看，我们也可以很自然的构造出Laughlin波函数。当然，这都是后话了~~~~~

完啦，/(ㄒoㄒ)/~~

（所有图，侵删）

来源：知乎 www.zhihu.com
作者：萨塔妮亚

【知乎日报】千万用户的选择，做朋友圈里的新鲜事分享大牛。点击下载

整数量子霍尔效应

第一部分：实验结果

第二部分：量子Hall电阻

第三部分：量子Hall电阻的普遍性

最后再说两句

有什么以上海为背景的书或影视剧？