自动控制总结：第三章：线性系统的时域分析

首先我们必须明白时域法是直接在时间域上对系统进行分析的方法，具有直观、准确的优点，它可以提供系统时间相应的全部信息。（该方法是最基本的方法，该方法引出的概念、方法、结论都是以后学习复域法、频域法等的基础）


控制系统的性能指标分为动态性能指标和静态性能指标。


在引入典型输入信号的原因是：控制系统的输入信号具有随机性，而如果在这个瞬态上获得系统的解析表达式，难以做到，因此希望有一些特殊的输入信号，通过这些输入信号以及其响应是一个非常不错的选择。


3.1

1、典型的输入信号

① 单位阶跃信号 对应的输出：单位阶跃响应

一般形式的阶跃函数：

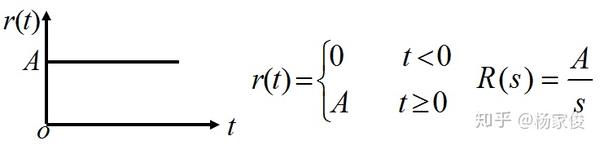
当A=1时，则为单位阶跃函数


②单位斜坡信号 对应的输出：单位斜坡响应

一般形式的斜坡函数

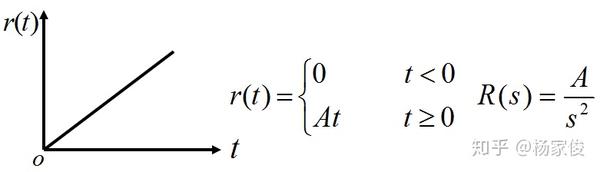
当A=1时则为单位斜坡函数


③单位脉冲信号 对应的输出：单位脉冲响应

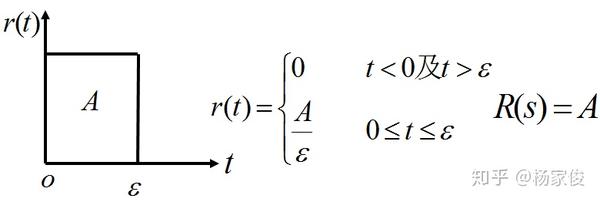
当A=1时为单位脉冲函数。


④单位加速度信号 对应的输出：单位加速度响应


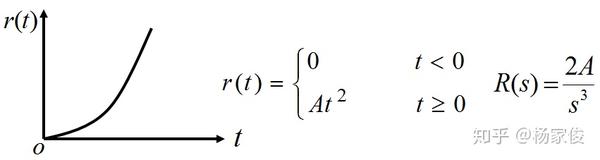
A=½时为单位抛物线函数


⑤正弦信号。


四种典型单位输入信号的关系



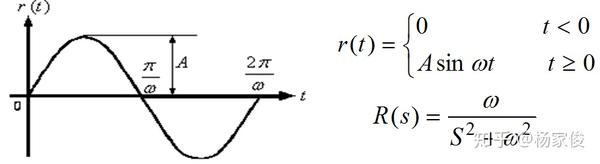
2、控制系统的时域性能指标

（1）响应过程分为动态过程和稳态过程

①动态过程：系统在典型信号的作用下，系统从初始状态到最终状态的过程

表现为衰减、发散和等幅振荡几种形式（系统要稳定正常工作，其动态过程必须衰减）

动态过程可以提供a、系统的稳定信息、b、响应速度c、阻尼情况

②稳态过程：系统在典型信号的作用下，时间t趋于无穷大的时候输出量的表现形式，

稳态过程提供了稳态误差的信息。


我们一般认为阶跃输入对系统而言是比较严峻的工作状态，所以如果系统在阶跃函数的作用下也能满足性能要求，那么其他情况也应该是令人满意的，因此系统的动态性能指标，均是在单位阶跃函数作用下测定计算的

并且在分析的时候，一般假定系统在阶跃信号作用前处于静止状态，而且系统输出量以及各阶导数均为零

（2）性能指标有以下：（全部都是以阶跃响应下定义）

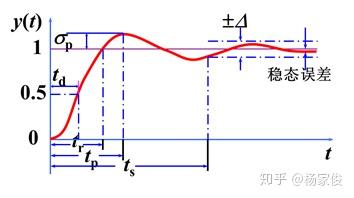
①延迟时间td：阶跃响应第一次达到终值C(∞)的50%所用的时间。

②上升时间tr：阶跃响应从终值的10%上升到终值的90%所需的时间，对有振荡的系统，也可以定义为从0到第一次到达终值所需的时间

③峰值时间tp：阶跃响应越过终值C(∞)到达第一个峰值所需的时间

④调节时间ts：阶跃响应到达并保持在终值C(∞)的±5%误差带内所需的最短时间。

有时候也用终值的±2%误差带来定义

⑤超调量σ%：峰值c（tp）超出终值c（∞）的百分比 即σ%=*100%


3.2一阶系统的时域分析

1、一阶系统的数学模型

例子：


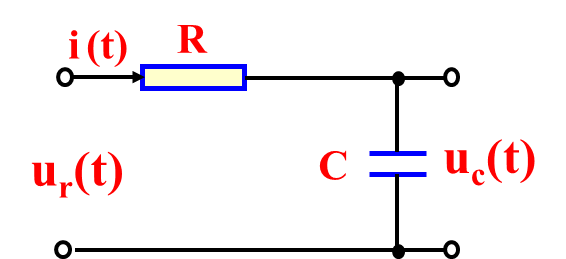
其微分方程为：T \frac{dc(t)}{dt} +c(t)=r(t)

拉氏变换后，传递函数为 Φ(S)= \frac{C(s)}{R(s)} = \frac{1}{Ts+1}

(T的含义随系统的不同而不同)

用方框图表示时有两种形式：

形式一：一阶系统

形式二：单位反馈一阶系统


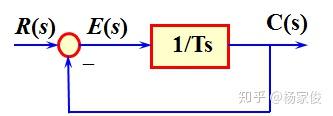
2、一阶系统的单位阶跃响应

r(t)=1(t) 拉氏变换后 R(S)=1/S

因此C(S)= Φ(S)R(S)=\frac{1}{Ts+1}* \frac{1}{s} 对这个式子进行拉氏反变换得：c(t)=1- e^{-t/T} (t≥0)

从c(t)的表达式中可以看到，初始值为0，终值为1

因此画出其响应曲线为


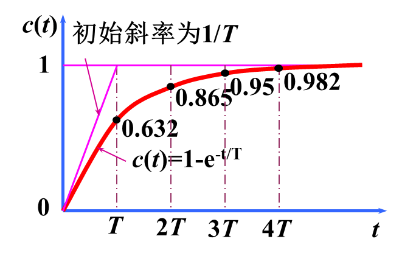
特点：

①当t等于T的整数倍时，即t=T，2T，3T，4T时候，响应的c(t)为总变化量的0.632、0.865、0.95、0.982倍，根据这个特点可以判断是否为一阶系统（这个要背背）

②t=0时候，输出相应的斜率为最大：

\frac{dc(t)}{dt} |_{t=0} = \frac{1}{T} e^{-t/T}|_{t=0}=\frac{1}{T}


进过计算我们可以得到一阶系统的动态性能指标为：td=0.69T，tr=2.20T，ts=3T

峰值时间tp和超调量σ%不存在，稳态误差ess=0。

记住这个：T值的大小反映系统的惯性。T值越小，惯性就越小，响应速度就快；T值大，惯性就大，相应速度就慢。这一结论也适用于一阶系统以外的系统（因为T越小，对应的ts就越小。）


3、一阶系统的单位脉冲响应

r(t)= δ(t) ， 其拉氏变换为R(S)=1

所以C(S)= Φ(S)R(S)=\frac{1}{Ts+1} 其拉氏反变换为 c(t)=\frac{1}{T} e^{-t/T} (t≥0)

其斜率公式\frac{dc(t)}{dt}=- \frac{1}{T^{2}}e^{-t/T} 所以\frac{dc(t)}{dt}|_{t=0}=- \frac{1}{T^{2}} , \frac{dc(t)}{dt} |_{t=∞}=0 （为什么要求斜率，其实是因为 就像高中学数学一样，从斜率可以大概看出它的函数规律）

调节时间按衰减到终值的5%求取 Ts=3T（T越小，响应速度越好）


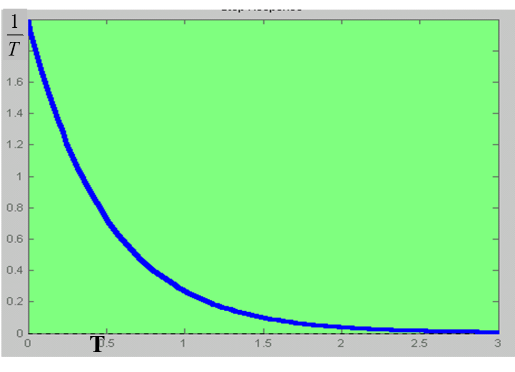
注：理想脉冲函数无法得到，因此往往以脉宽为b、幅值有限的脉动函数代替理想单的脉动函数δ(t)，而且要求脉宽b＜0.1T。


4、一阶系统的单位斜坡响应

r(t)=t， 其拉氏变换 R(S)= \frac{1}{s^{2}} ，

C(S)= Φ(S)R(S)=\frac{1}{Ts+1}*\frac{1}{s^{2}} 其拉氏反变换为c(t)=t-T+Te^{-t/T}

其中 t-T为稳态分量：其与斜坡输入函数的斜率相同，但在时间上之后一个T，因此存在位置误差，

Te^{-t/T}为瞬态分量：随着时间单调衰减


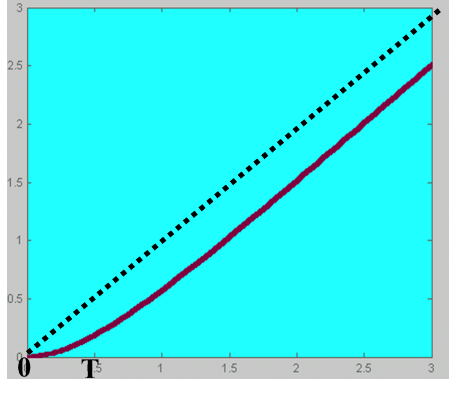
特点：

①系统的输出量和输入量之间的位置误差随时间推移逐渐增大，但最后趋向于T。因此，T越小，位置误差越小。

②在t=0时，初始实线的斜率为0 (\frac{dc(t)}{dt}|_{t=0}=1-e^{-t/T}|t|_{t=0}=0)

因此初始状态的输出速度（实线斜率）和输入速度（虚线斜率）之间误差最大


5、一阶系统的单位加速度响应

r(t)= \frac{t^{2}}{2} 其拉氏变换为R(S)= \frac{1}{s^3} .

因此C(S)= Φ(S)R(S)=\frac{1}{Ts+1}* \frac{1}{s^3} 其拉氏反变换为c(t)=\frac{t^{2}}{2}-Tt+ T^{2} (1-e^{-t/T})

跟踪误差e(t)=r(t)-c(t)= \frac{t^{2}}{2}-[\frac{t^{2}}{2}-Tt+ T^{2} (1-e^{-t/T})]=Tt- T^{2} (1-e^{-t/T})

当t趋向于∞时，e(t)趋于无穷大，因此得出一阶系统无法跟踪加速度信号


3.3二阶系统的时域分析

用二阶微分方程描述的系统称为二阶系统，其应用广泛，甚至许多高阶系统在一定条件下可以用二阶系统表示。


  1. 二阶系统的数学模型

书本上一开始就来了一个RLC电路，推导出一个二阶系统的模型，



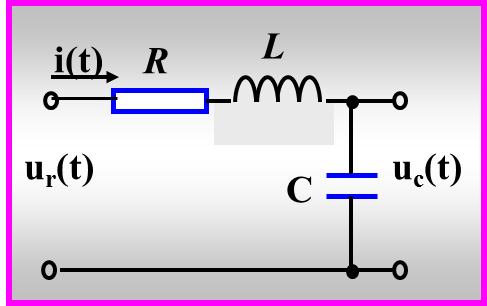
其微分方程为 LC\frac{d^{2}c(t)}{dt^{2}}+RC\frac{dc(t)}{dt}=+c(t)=r(t)


所以其传递函数为 Φ(S)= \frac{C(s)}{R(s)} = \frac{1}{LCs^2+RCs+1}

我们对这个传递函数标准化（标准化后，参数有具体意义），就可以得到

Φ(S)=\frac{C(s)}{R(s)}=\frac{1}{s^2+2ζw_{n}s+w_{n}^2}

其中wn= \frac{1}{\sqrt{LC}} 称为自然频率，单位rad/s， ζ＝ \frac{R}{2} \sqrt{\frac{C}{L}} 称为二阶系统的阻尼比，无量纲

其开环传递函数为 G(S)= \frac{w_{n}^2}{s(s+2ζw_{n})}


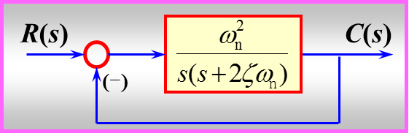
令闭环传递函数的分母多项式为0，其闭环系统的特征方程 s^{2} +2ζ w_{n} s+ w_{n}^{2} =0

得出其根（闭环极点）为 S_{1,2} =-ζ w_{n} ± w_{n} \sqrt{ζ^2-1}

通过分析不同的ζ情况，得出不同的特征根状况

①欠阻尼：0＜ζ＜1 S1,2=-ζ w_{n} ±j w_{n}\sqrt{1-ζ^2}

②无阻尼：ζ=0 S1,2=±j w_{n}

③临界阻尼：ζ＝1 S1,2=- w_{n}

④过阻尼：ζ>1 S1,2=-ζ w_{n} ± w_{n}\sqrt{ζ^2-1}


2、二阶系统的单位阶跃响应

r(t)=1 R(S)= \frac{1}{s}

（1）欠阻尼 （0＜ζ＜1）

S1,2==-ζ w_{n} ±j w_{n}\sqrt{1-ζ^2}=-ζ w_{n} ±j w_{d}

（其中令w_{d}=w_{n}\sqrt{1-ζ^2}，这条公式一定要记住,wd称为阻尼振荡频率）

所以输出C(S)= Φ(S)R(S)=\frac{1}{s^2+2ζw_{n}s+w_{n}^2}*\frac{1}{s}

=\frac{1}{s}-\frac{s+2ζw_{n}}{s^2+2ζw_{n}s+w_{n}^2}=\frac{1}{s}- \frac{s+ζw_{n}}{(s+ζw_{n})^2+w_{d}^2} - \frac{ζw_{n}}{(s+ζw_{n})^2+w_{d}^2}

拉氏反变换为 ：

c(t)=1- e^{-ζw_{n}t} (cos w_{d} t- \frac{ζw_{n}}{w_{d}} sin w_{d} t) =1- e^{-ζw_{n}t} (cos w_{d} t- \frac{ζ}{\sqrt{1-ζ^2}} sin w_{d} t)

=1- \frac{e^{-ζw_{n}t}}{\sqrt{1-ζ^2}} sin(w_{d} t+β)

式中β＝arctg \frac{\sqrt{1-ζ^2}}{ζ} （β也等于arccosζ） 称为滞后角

（记忆方法：cosβ＝ζ，sinβ＝ \sqrt{1-ζ^2} ）

从c(t)的式子看，发现其由稳态和瞬态两部分组成，稳态部分等于1，表明不存在稳态误差（1-r(t)=0），瞬态部分是阻尼振荡，阻尼的大小由ζ w_{n} (即特征根实部ζ w_{n}=σ ）决定；


ζ越小，超调量越大


（2）无阻尼（ζ=0）

C(t)=[1- e^{-ζw_{n}t} (cos w_{d} t- \frac{ζ}{\sqrt{1-ζ^2}} sin w_{d} t)] |_{ζ=0} =1- cost w_{n}（把ζ=0带入欠阻尼那条式子即可） （此时wn=wd）



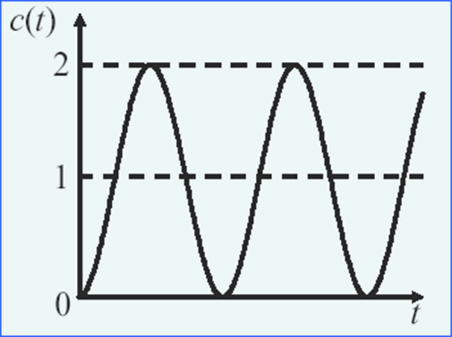
响应曲线：此时为等幅振荡


（3）临界阻尼（ζ=1）

C(t)=[1- e^{-ζw_{n}t} (cos w_{d} t- \frac{ζ}{\sqrt{1-ζ^2}} sin w_{d} t)] |_{ζ=1} =1- e^{-w_{n}t}(1+w_{n}t) （t≥0）（一样的把ζ＝1带入欠阻尼那条式子）（第三项计算的时候要用洛必达就可以得到那个结果了）



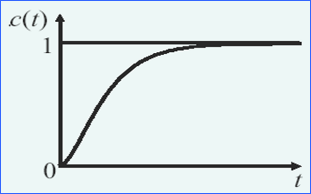
响应曲线：单调上升，无振荡，无超调，无稳态误差


（4）过阻尼（ζ＞1）

C(S)= \frac{w_{n}^2}{s(s+ζw_{n}-w_{n}\sqrt{ζ^2-1})(s+ζw_{n}+w_{n}\sqrt{ζ^2-1}))}

因此对其作拉氏反变换

c(t)=1- \frac{1}{2\sqrt{ζ^2-1}(ζ-\sqrt{ζ^2-1})}e^{-(ζ-\sqrt{ζ^2-1})w_{n}t} +\frac{1}{2\sqrt{ζ^2-1}(ζ+\sqrt{ζ^2-1})}e^{-(ζ+\sqrt{ζ^2-1})w_{n}t}

=1+ \frac{e^{-t/T_{1}}}{T_{2}/T_{1}-1} +\frac{e^{-t/T_{2}}}{T_{1}/T_{2}-1}（t≥0）

T1、T2成为过阻尼二阶系统的时间常数，而且T1＞T2

如果ζ>>1时，可以把-1/T2指数项的分量忽略，这样过阻尼的相应类似于一阶系统的相应


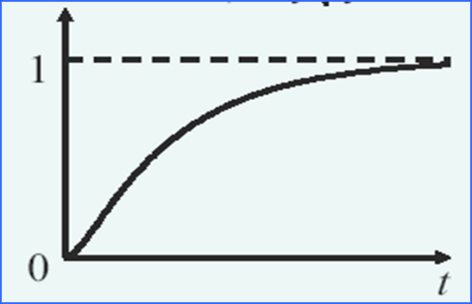
响应曲线：单调上升，无振荡，过渡过程时间长，无稳态误差。


（5）负阻尼（ζ＜0）

其有一对共轭复根，且极点实部大于零

响应有两种状态，一种是振荡发散，一种是单调发散


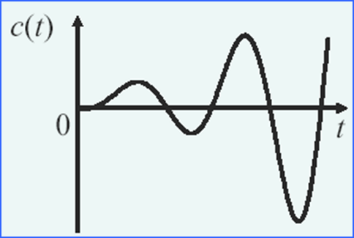
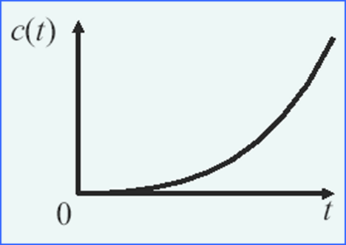
由于系统此时不能正常工作，那么研究也就没有意义了。


小结：阻尼比决定了系统的振荡特性

  1. ζ＜0 时（负阻尼），响应发散，系统不稳定；
  2. ζ=0时（无阻尼），等幅振荡
  3. 0＜ζ＜1时（欠阻尼），有振荡，ζ越小，振荡越严重，但响应越快
  4. ζ≥1时（过阻尼和临界阻尼），无振荡，无超调


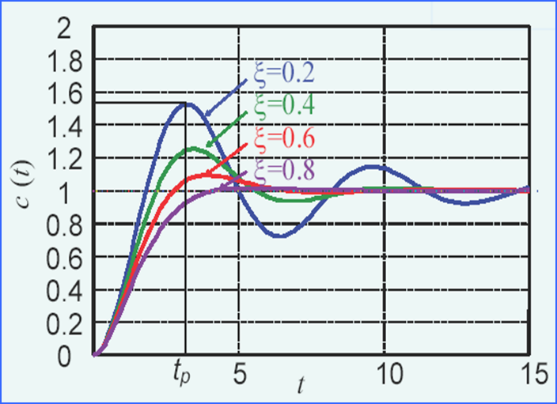
除不允许产生振荡的系统，通常采用欠阻尼状态，阻尼比选择在0.4~0.8之间，保证系统有好的运动动态。（此时响应曲线超调量合适，调节时间短）

还必须注意，ζ＜0.4时，会使超调量较大，ζ＞0.8时，又会使响应迟缓

（这里判断的时候，紧紧记住那个好多ζ的图就好）


ζ一定时，ωn越大，瞬态分量衰减越快，系统能更快达到稳态值，系统的快速性越好

（这是因为wn在指数部分且带一个负号，所以其越大，衰减越快）


3、欠阻尼二阶系统的动态过程分析

回忆一下动态指标：tr、 tp 、σp%、ts 。


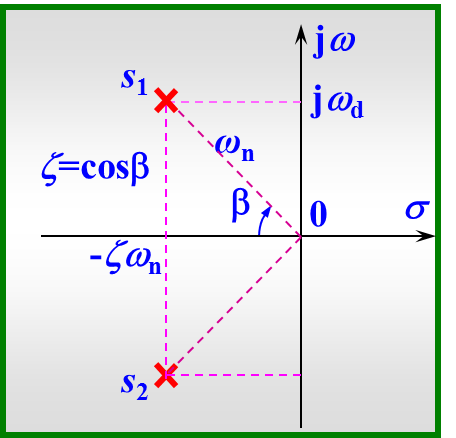
图中 衰减系数σ指闭环极点到虚轴之间的距离，阻尼振荡频率为闭环极点到实轴的距离，自然频率是闭环极点到原坐标之间的距离，与负实轴的余弦是阻尼比，即ζ＝cosβ


（1）上升时间

根据定义，令c(t)=1,得\frac{e^{-ζw_{n}t}}{\sqrt{1-ζ^2}} sin(w_{d} t+β)=0，因为 e^{-ζw_{n}t} ≠0，所以sin( w_{d}t_{r} +β)=0

解得 w_{d}t_{r}+β=kπ，由于tr的定义是第一次到达的时间，所以取k=1，则得到

上升时间为 t_{r} = \frac{π－β}{w_{d}} = \frac{π-arccosζ}{w_{n}\sqrt{1-ζ^2}}

从式中可以看出，当ζ一定时，β不变，系统的相应速度和wn成正比

当阻尼振荡频率wd一定时，ζ越小，上升时间越短


（2）峰值时间

对c(t)求导 \frac{dc(t)}{dt}|_{t=tp} =0

所以得\frac{e^{-ζw_{n}tp}}{\sqrt{1-ζ^2}}w_{n} sin(w_{d} tp+β-β)=0 因为\frac{e^{-ζw_{n}tp}}{\sqrt{1-ζ^2}}w_{n} ≠0，所以有sin(w_{d} tp+β-β)=0

所以，w_{d} tp=2kπ，取k=1得

tp= \frac{π}{w_{d}} = \frac{π}{w_{n}\sqrt{1-ζ^2}}

式子说明峰值时间等于阻尼振荡周期的一半，ζ一定时，wn越大，tp越小


（3）超调量σ%：

最大超调量发生在峰值时间tp时，把其带入c(tp)，得到c(tp)= 1- \frac{e^{-πζ/\sqrt{1-ζ^2}}}{\sqrt{1-ζ^2}} sin(π+β)

因为sin(π+β)=- \sqrt{1-ζ^2} （这是因为sinβ=\sqrt{1-ζ^2}） 所以可以写成c(tp)=1+ e^{-πζ/\sqrt{1-ζ^2}}

又由于终值为1，所以得

最大超调量百分比 σ%=e^{-πζ/\sqrt{1-ζ^2}}= e^{-πcotβ}

ζ越大，从而β越小，所以cotβ越大，所以超调量越小，

当ζ在0.4-0.8范围内时，σ%在1.5%~25.4%之间


  1. 调整时间ts ：回忆一下， 单位阶跃响应进入±△误差带的最小时间

ts= \frac{3.5}{ζw_{n}}


小结：

  1. 二阶系统的动态性能由w_{n} 和ζ决定
  2. 增加ζ：a、降低振荡（即ts减小），减少超调量 b、系统的快速性能降低，tr、tp增加。
  3. ζ一定，wn越大，系统响应快速性越好，tr、tp、ts越小
  4. 超调量仅与ζ有关，而tr、tp、ts与ζ、wn有关


4、二阶系统的性能改善

(1)比例—微分控制

其结构图：Td为微分时间常数，比例因子是1，E(s)为误差信号




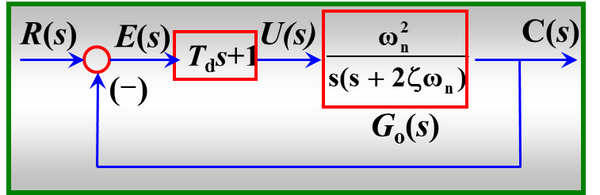
开环传递函数：G(S)= \frac{C(s)}{E(s)} =\frac{w_{n}^2}{s(s+2ζw_{n})}(T_{d}s+1)= \frac{K(T_{d}s+1)}{s(\frac{s}{2ζwn}+1)} 其中K为 \frac{w_{n}}{2ζ}

闭环传递函数： Φ(S)= \frac{C(s)}{R(s)} = \frac{s+z}{s^2+s(ζ+w_{n}\frac{T_{d}}{2})w_{n}s+w_{n}^2} * \frac{w_{n}^2}{z} （令z=1/ T_{d} ）

增加一个闭环零点 -z=-1/ T_{d} 阻尼比增大 ζ_{d} =ζ+ \frac{T_{d}w_{n}}{2} =ζ+ \frac{w_{n}}{2z}

特点：

①引入比例-微分控制，阻尼比增加，从而抑制振荡，使超调减弱，改善系统平稳性；

②闭环零点的出现，既加快系统响应速度，使上升时间缩短，峰值提前，又削弱了"阻尼"作用。适当选择微分时间常数Ｔd，使系统既有较好的平稳性，又在出现较小超调情况下，提高快速性。

③不影响系统误差，自然频率不变


单位阶跃信号作用下的输出响应

C(S)= Φ(S)R(S)= \frac{w_{n}^2}{(s^2+2ζ_{d}w_{n}s+w_{n}^2)s} +\frac{w_{n}^2}{s^2+2ζ_{d}w_{n}s+w_{n}^2}*\frac{1}{z}

其输出相应为 c(t)=1+r e^{-ζ_{d}w_{n}t} sin(wn \sqrt{1-ζ_{d}^{2}} t＋φ)

r=\sqrt{z^2-2ζ_{d}w_{n}+w_{n}^2}/z\sqrt{1-ζ_{d}^{2}}，

φ=-π+arctan[wn\sqrt{1-ζ_{d}^{2}}/(z- ζ_{d}w_{n} )]+arctan(\sqrt{1-ζ_{d}^{2}}/ζd)

部分性能指标：

峰值时间tp：对c(t)求导，令其为0，

得tp= \frac{β_{d}-φ}{w_{n}\sqrt{ 1-ζ_{d}^2}} ，其中βd=arctan(\sqrt{1-ζ_{d}^{2}}/ζd)

超调量σ%：σ%=r*\sqrt{1-ζ_{d}^{2}} e^{-ζ_{d}t_{p}/\sqrt{1-ζ_{d}^2}}

调节时间ts： \frac{3+\frac{1}{2}ln(z^2-2ζ^{d}w_{n}+w_{n}^2)-lnz-\frac{1}{2}ln(1-ζ_{d}^2)}{2ζ_{d}w_{n}}


（2）测速反馈控制



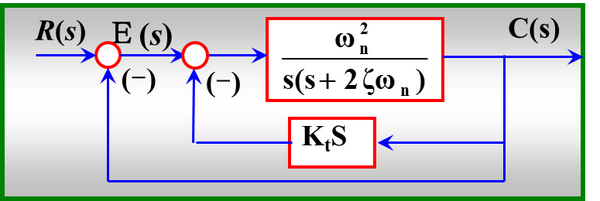
开环传递函数：G(S)=\frac{w_{n}^2}{s^2+s(2ζw_{n}+k_{t}w_{n}^2)}=\frac{K}{s[s/(2ζw_{n}+K_{t}w_{n}^2)+1]}

其中K= \frac{w_{n}}{2ζ+K_{t}w_{n}}

闭环传递函数：Φ(S)= =\frac{w_{n}^2}{s^2+2ζ_{t}w_{n}s+w_{n}^2} 式中阻尼比ζt =ζ+½ K_{t}w_{n}


两种控制系统比较如下:

(1)开环增益K，比例—微分控制不改变开环增益K 。

(2)wn不变，阻尼比增大。分别为

ζt=ζ+ \frac{K_{t}w_{n}}{2} ，ζd=ζ+ \frac{T_{d}w_{n}}{2} 当Kt=Td时，两者相等 。

（3）比例—微分控制提供一个实零点，在相同的阻尼比时，超调量大于测速反馈控制。

（4）比例—微分控制对输入噪声有放大作用，输入端高频噪音严重时，不宜选用此方法。测速反馈控制无需设置放大器，适合任何输出可测的控制系统。

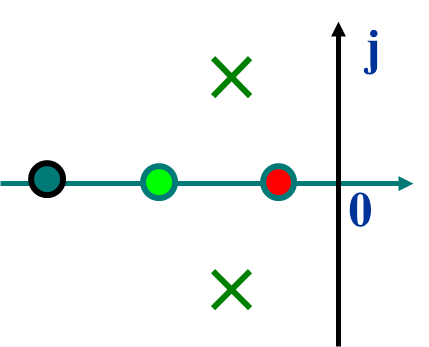
5、附加零点对欠阻尼二阶系统的影响

附加一个闭环零点，超调量上升，上升时间下降，峰值时间下降。





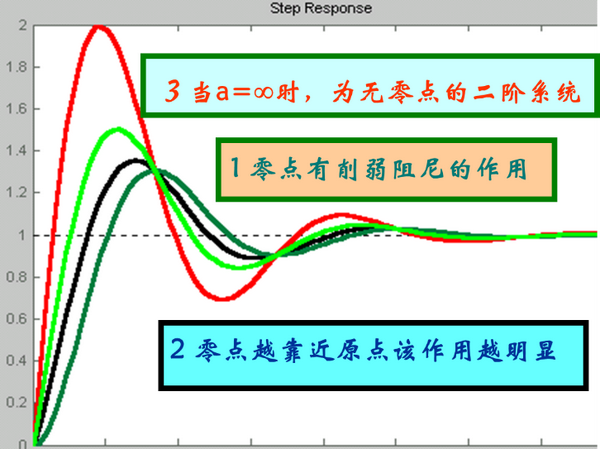
附加零点对过阻尼二阶系统的影响




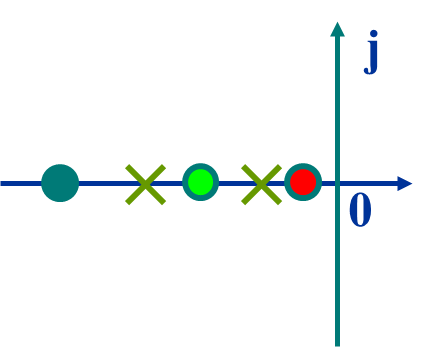
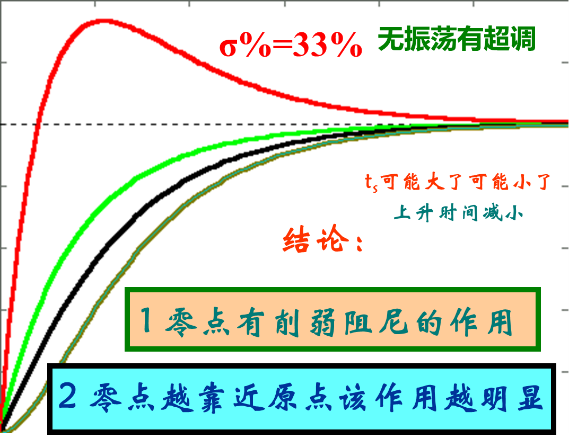
附加极点对系统的影响





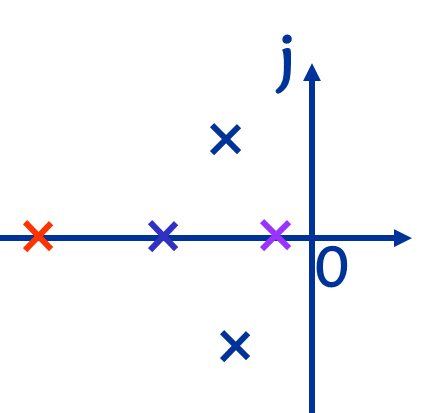
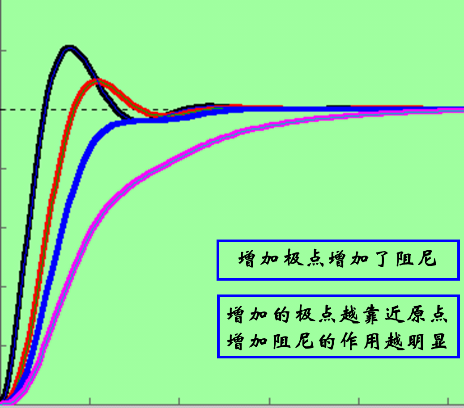
对所有的二阶系统，增加零点,削弱阻尼,超调变大,上升时间变短,调节时间不一定小。



3.4线性系统的稳定性分析

1、系统稳定的条件：系统初始条件为0时，受到δ(t)的作用，输出c(t)为单位脉冲响应，这相当于系统在扰动的作用下，输出信号偏离平衡点的问题，当t→∞时，

若=0-------------------系统稳定

若=∞------------------系统不稳定

若=A（A为非零常数）---临界稳定

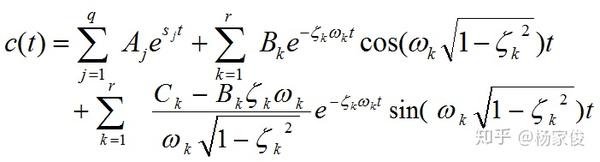
（t≥0）


系统稳定的充分必要条件：系统特征方程的根全部具有负实部，即闭环系统的极点全部在s平面左半部。


注：稳定性与零点无关


  1. 劳思稳定判据

其特点是要知道系统的闭环传递函数，其线性系统的闭环特征方程为



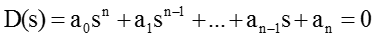
用例子去说明，


讨论特殊情况一，因为第一列元素会作为分母，当第一列出现0时，要用一未知量代替


特殊情况二，出现全行都是0



3.5 线性系统的稳态误差

1、误差的基本概念

系统的误差通常用两种方法定义：

（1）按输入端定义：



E(s)=R(s)-B(s)=R(s)-C(s)H(s)

（2）按输出端定义




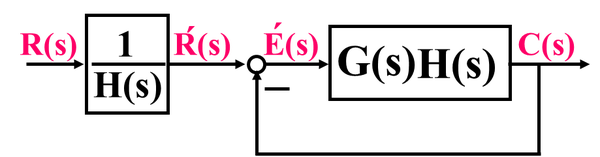
E'(S)=R(S)/H(S)-C(S)

按输入端定义的误差E(S)通常在实际系统中可以测量，具有一定的物理意义，但误差理论的含义部十分明显，按系统输出端定义误差是希望输出与实际输出C(s)之差，比较接近误差的理论意义。但通常不可测量


两种误差定义之间的关系是：E'(S)=E(s)/H(s)


2、计算误差的一般方法

最常用的就是终值定理法，该方法适合各种情况下的稳态误差计算，以下说明步骤

①判定系统的稳定性：稳定是系统正常工作的前提条件，否则稳态误差没有意义

②求误差传递函数：Φe= \frac{E(s)}{R(s)} = \frac{1}{1+G(s)H(s)} 公式由来：R(S)-E(S)*G(S)H(S)=E(S)

误差信号e(t)是E(S)的拉氏反变换 ，其由瞬态分量 ett(t)和稳态分量ess(t)两部分组成

由于系统必须稳定，所以t→∞时，ett(t)＝0，所以稳态误差就是ess(t)


用终值定理求稳态误差：ess= \lim_{s \rightarrow 0}{sE(s)}

终值定理应用条件是sE(s)在右半平面及虚轴上解析，即sE(s)几点全部为s平 面左半平面。当系统不稳定或者R(S)的几点由于虚轴上以及虚轴右边时，该条件不满足




这个系统的稳态误差ess= \lim_{s \rightarrow 0}{sE(s)}= \lim_{s \rightarrow 0}{sΦe(s)R(s)}=\lim_{s \rightarrow 0}{s*\frac{R(s)}{1+G(s)H(s)}}


3、系统型别

设开环传递函数G(s)H(s)= \frac{K\prod_{i=1}^{m}(τ_{i}+1)}{s^v\prod_{j=1}^{n-v}(T_{j}s+1)}

式中K为开环增益，和为时间常数，v为开环积分环节的数目，称为系统的型别或无差

度。按v的不同，系统分类如下：

V=0，称为0型系统，或有差系统

V=1，称为Ⅰ型系统，或一阶无差系统

V=2，称为Ⅱ型系统，或二阶无差系统

V＞2，除复合控制外，系统难以稳定，在此不做讨论

令=，则当s→0时，有→1

因此G(s)H(s)= \frac{K}{s^v}G_{0}(s)H_{0}(s)

所以Φe= \frac{E(s)}{R(s)} = \frac{1}{1+\frac{K}{s^v}G_{0}(s)H_{0}(s)} 所以ess= \lim_{s \rightarrow 0}{sΦe(s)R(s)}= \frac{\lim_{s \rightarrow 0}{s^{v+1}R(s)}}{K+\lim_{s \rightarrow 0}{s^v}}


4、静态误差系数

①阶跃输入 r(t)=A*1(t)，则R(S)=A/S，A是阶跃函数的幅值。

所以ess= \lim_{s \rightarrow 0}{sΦe(s)R(s)}= \lim_{s \rightarrow 0}{s*\frac{1}{1+G(s)H(s)}*\frac{A}{s}}= \frac{A}{1+\lim_{s \rightarrow 0}{G(s)H(s)}}

定义：静态位置误差系数：Kp== \lim_{s \rightarrow 0}{sG(s)H(s)}== \lim_{s \rightarrow 0}{\frac{K}{s^v}}

(根据系统型别那部分内容去理解)

因此：


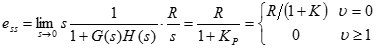
因此，要为0，则用I型以上系统，0型系统在阶跃输入下存在非零的稳态误差


②斜坡输入 r(t)=At，A为斜坡输入函数的斜率

ess= \lim_{s \rightarrow 0}{sE(s)}= \lim_{s \rightarrow 0}{sΦe(s)R(s)}=\lim_{s \rightarrow 0}{s*\frac{1}{1+G(s)H(s)}*\frac{A}{s^2}}=(因为分母那里1那一部分乘以s之后，s趋向于0时那部分趋向于0，所以有) = \frac{A}{\lim_{s \rightarrow 0}{sG(s)H(s)}}

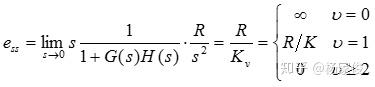
定义：静态速度误差系数： K_{v} = \lim_{s \rightarrow 0}{sG(s)H(s)} =\lim_{s \rightarrow 0}{\frac{K}{s^{v-1}}}


因此选Ⅱ型以上系统不存在稳态误差，选用Ⅰ型系统存在有限误差，表明稳态输出时的速度和输入速度相同（因为是相减），0型系统不能跟踪斜坡输入


③加速度输入 r(t)=A \frac{t^2}{2} ，A是加速度输入函数的速度变化率

ess= \lim_{s \rightarrow 0}{sE(s)}= \lim_{s \rightarrow 0}{sΦe(s)R(s)}=\lim_{s \rightarrow 0}{s*\frac{1}{1+G(s)H(s)}*\frac{A}{s^3}}= (这里也一样把s^2那部分略去)= \frac{A}{\lim_{s \rightarrow 0}{s^2G(s)H(s)}}

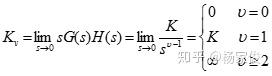
定义静态加速度误差系数 K_{a} = \lim_{s \rightarrow 0}{s^2G(s)H(s)} =\lim_{s \rightarrow 0}{\frac{K}{s^{v-2}}}


假设系统的输入信号是多种典型函数的组合，例如r(t)=(A+Bt+C)*1(t)那么可根据线性叠加原理求解稳态误差,ess= \frac{A}{1+K_{p}} + \frac{B}{K_{v}} + \frac{c}{k_{a}}

小结



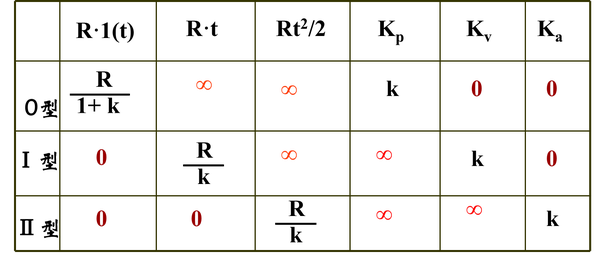
从中我们可以看到，增大K，那么就减小，如果增加开环传递函数中的积分环节，那么就可以消除稳态误差（例如在对于Ⅰ型系统，输入斜坡信号会有误差，但是增加积分环节，使其提升到Ⅱ级系统以上，那么就误差就为0）

6、扰动作用下的误差



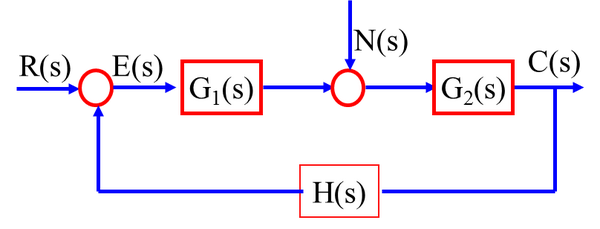
essn= \lim_{s \rightarrow 0}{sΦen(s)N(s)} = \lim_{s \rightarrow 0}{s*\frac{-G_{2}(s)H(s)}{1+G_{1}(s)G_{2}(s)H(s)}}*N(s) =N(S)

当| G_{1}(s)G_{2}(s)H(s) |>>1，有essn= \lim_{s \rightarrow 0}{s*\frac{-N(s)}{G_{1}(s)}}

大家可以评论相关自动控制的问题，我也会耐心给你们解答的(#^.^#)

以上内容未经本人同意禁止转载~~



来源：知乎 www.zhihu.com
作者：杨家俊

【知乎日报】千万用户的选择，做朋友圈里的新鲜事分享大牛。 点击下载
时间： 没有评论:

青霉素传奇续：人类死亡率转变的重大拐点

►图片来源：Pixabay.com

●●●

开发（二） 资金

让我们的目光继续凝视着1940年的英国。邓恩学院的实验团队需要越来越多的青霉素。这个问题必须靠希特利去解决，而且前提是实验室几乎没有任何资金。

实验室一直被钱的问题所困扰。科研在当时主要有两种资助模式：工业模式和慈善模式。德国制药业是工业模式的典范。20世纪上半叶，在莱茵河两岸集中着德国的几大制药行业巨头，他们起家于染料公司，从染料扩展到化工，又由化工进入到医药。他们资金雄厚，在化学合成方面独步世界。保罗·埃尔利希（Paul Ehrlich）和Hoechst AG公司的申凡纳明（Salvarsan, 治疗梅毒的首个有效药）、多马克博士和拜耳公司的磺胺药就是在德国工业模式下成功开发的产品。

而邓恩学院资金的来源主要靠捐赠，包括来自个人和洛克菲勒基金会，只有极少部分来自英国政府（英国医学研究委员会）。而英国的制药公司财力远逊于德国的公司，并且对青霉素项目不感兴趣。由于二战，政府能提供的资金非常有限。医学研究委员会每年提供的研究基金仅为300到550英镑。即使来自洛克菲勒基金会的资金也远远不够，比如在1936年基金会一次性提供了购买精密仪器的资金只有250英镑。钱恩的年薪只有200英镑，持续的经济窘境使他长期处于焦虑状态。直到1939年，实验室的经济情况才稍微好转一些。洛克菲勒基金会那年提供了1300英镑的资助，其中有300英镑是希特利的薪水。

实验室在各项开销上能省就省。为了每年节省25英镑，弗洛里关闭了楼里的电梯。实验室的旧冰箱以前是手动的——如果看管人觉得冰箱温度高了，就把压缩机打开开始制冷。钱恩负责扩大和改造冰箱，最后花销超出预算15英镑。为此事弗洛里大发雷霆，并在随后的数年里时不时地跟钱恩提起此事，直到1948年钱恩离开邓恩学院。

虽然在资金困窘的条件下最能展现希特利的心灵手巧，但在遇到特别棘手的问题时，希特利也只能采取极端手段。为了培养足够量的青霉菌，希特利需要足够大的容器。于是学院厨房里的烤盘和糕点器皿总是莫名其妙地丢失。16个便盆神秘地从距离病理实验室1.5英里的牛津大学医院消失，又神秘地出现在病理实验室里。



荣誉和冲突

1940年8月24日，弗莱明论文发表之后又过了11年零5个月，几乎在德军轰炸机开始大规模地出现在伦敦上空的同时，弗洛里团队的关于青霉素的论文在著名医学期刊"柳叶刀"上发表。论文只有短短两页，描述了青霉素在小鼠实验中对葡萄球菌，链球菌和梭菌等病原体引起的感染的疗效。

弗洛里团队成员之间一直有着各种冲突。弗洛里要花很大精力平衡内部的各种关系。在经历了几次对论文署名顺序的激烈争论后，弗洛里干脆规定实验室的所有论文的作者按姓名字母顺序排序。这篇"柳叶刀"论文就是这样的。1941年弗洛里和希特利因为青霉素扩大化生产一事去美国。弗洛里没有带上钱恩，甚至都没有事先通知他。虽然美国之行和钱恩的工作关系不大——他的主要任务是结晶青霉素，解决它的化学结构，钱恩还是大为恼火。他已经意识到青霉素有可能让他得诺贝尔奖。他最大的担心是弗洛里把他的荣誉夺走。作为一个犹太裔移民，他对自己有可能受到的不公平待遇极为敏感。（钱恩在战后才知道，他在德国的母亲和妹妹于1942年死于纳粹集中营里。）他从未信任过弗洛里，而弗洛里对他的态度也一直很恶劣。

使事情更为复杂的是，弗洛里的夫人和情人都在他的实验室里工作。大家基本是捏着鼻子容忍着彼此，竟然创造了改变世界的成果。

青霉素引起了媒体的注意，也引发了对这一成果的荣誉的争夺。40年9月2日，59岁的弗莱明突然出现在邓恩学院。据他说，他是想来看看用"我的旧青霉素"已经做了什么。钱恩大吃一惊，"天啊，他还活着？！"

临床

1941年1月，希特利的"作坊"已经生产出足够多的青霉素，甚至达到了用到病人身上的量。服用青霉素的第一个志愿者是Elva Akers, 一个癌症晚期病人。在注射了100毫克青霉素后，Akers几乎立刻发高烧，并不时有癫痫发作。弗洛里和同事们的心都沉到了谷底。但钱恩和另一位化学家亚伯拉罕很快找到原因。引起Akers发烧的并不是青霉素，而是样品中混有的杂质。他们又用更严格的提纯方法——将样品反复过层析柱——制备了更纯的样品。第二次注射后，Akers没有任何不良反应，既不发烧也不颤抖。

青霉素在人体的安全性被初步证明，下一步要看它的疗效了。用青霉素治疗的第一个病人是阿尔伯特•亚历山大（Albert Alexander）。他是一个警察，1940年9月在自己家的玫瑰花园干活时被花刺划破脸。细菌——至少包括链球菌和葡萄球菌——的感染先从伤口开始，进而扩散到头皮。他住院后，尽管服用了磺胺药，病情还是越来越严重，感染已进到了肺部。到41年2月，亚历山大浑身流脓，甚至左眼都有脓肿。他后来很快失去了左眼。

2月12日，200毫克的青霉素液（很久以后医生们才知道，这时样品的青霉素浓度不到5%）通过静脉注射进入到亚历山大的体内，之后每隔3小时再注射100毫克。仅过了一天，亚历山大已经有了惊人的改善：他的烧退了，不流脓了，脸也不肿了。他甚至可以进食了。

问题是实验室生产青霉素的速度远远比不上病人消耗的速度——病人一小时的剂量需要希特利的机器连续运转几天制备。弗洛里团队通过小鼠实验知道，青霉素可以很快通过尿液排到体外，尿中的青霉素仍有活性。所以医生每次给药后又多了一步，收集亚历山大的尿，再用自行车送到邓恩实验室回收青霉素。（是的，这家医院就是一年前16个便盆不翼而飞的那家。）

与亚历山大同期接受青霉素治疗的还有另外一个病人，亚瑟•琼斯（Arthur Jones）, 一个15岁的男孩儿。他是因为臀部手术而受到感染。他和亚历山大接受同样的疗程、同样的剂量。到2月底，所有的青霉素，包括回收的，都用光了。琼斯活下来了，而亚历山大没有。他于3月15日病逝。

在1941年的夏天，牛津团队用青霉素治疗了更多的病人——主要以儿童为主，因为儿童需要的剂量小。

要想进行更大的临床实验，要想用青霉素挽救更多的生命，仅靠邓恩实验室显然是不行的。下一轮扩大的临床试验就需要数千克的纯青霉素。在整个英国也找不到这种生产能力。在二战的战火席卷欧洲大陆时，世界上只有一个地方可以将青霉素产业化——美国。

产业化 美国之行和北方实验室

1941年7月2日，在洛克菲勒基金会的资助下，弗洛里和希特利几经周折，到达美国东海岸，寻求解决青霉素工业化生产的问题。他们随身携带的最大的一笔财富是几小瓶青霉素粉和青霉菌孢子。在这次高效率的行程中，通过朋友的介绍和洛克菲勒基金会的牵线，他们有机会和几个关键人物见面讨论，包括美国国家研究委员会执行委员会主席罗斯•哈里森 （Ross Harrison）、美国农业部植物工业局的一名真菌学家Charles Thom、美国科学研究与发展办公室（OSRD）的医学研究委员会（CMR）主席里查兹（Alfred Newton Richards）。

当时美国领先世界的是农业。农场、森林和牧场占全国经济的20%。与农业有关的科研项目和实验室遍布全国，但最著名的是农业部的四大科研中心。7月14日，弗洛里和希特利拜访了位于伊利诺州皮奥里亚市（Peoria, Illinois）的北方地区研究实验室（简称"北方实验室"），四大中心之一。在随后的几年里，北方实验室将完成将青霉素产业化最迫切的三项任务：1）找到了产率最高的青霉菌菌株; 2）找到最佳培养基配方，缩短霉菌的生长周期; 3）改善发酵技术。用传统农业打比方的话，他们找到了"更好的种子，更好的土壤，更好的种植和收获技术"。

"更好的种子" 在弗洛里访问之前，北方实验室已经通知科研人员在全世界范围寻找、收集不同菌株的青霉菌。但产率最高的菌株是实验室内部的一名叫玛丽•亨特（Mary Hunt） 实验员找到的。她经常去逛皮奥里亚的农贸市场, 看到发霉的水果和蔬菜就两眼放光。1943年，她中了大奖, 淘了一个发霉的哈密瓜。20世纪40年代末期，世界上几乎所有青霉素都来自那个哈密瓜上的霉菌及其后代。

"更好的土壤" 在寻找最适培养基配方的过程中，北方实验室也比较运气。在四十年代，美国盛产玉米。北方实验室的一个主要任务是找到玉米等过剩农作物的工业用途。玉米浆是制玉米淀粉的副产物。实验室的微生物和真菌学家安德鲁•莫耶（Andrew Moyer）和远道而来的希特利合作, 在几周之内发现玉米浆加上糖竟然能将青霉素的产率提高了一千倍!（但希特利又一次受到不公平的待遇: 莫耶后来在相关的论文和专利上只属了自己的名字，而故意省略掉希特利的名字。）

"更好的种植和收获技术" 青霉菌通过发酵产生青霉素（二级代谢产物）。但迄今为止，青霉菌只在培养基（通常是琼脂）表面发酵。青霉素的生产受二维平面的限制，即使把培养基铺成足球场那么大，产量也有限。北方实验室发酵部门的负责人罗伯特·科格希尔（Robert Coghill）首先提出了把酿造啤酒的深度发酵法照搬过来，从二维变成三维培养。深度发酵法已经被辉瑞用来生产柠檬酸。但与生产啤酒或柠檬酸不同的是，青霉素发酵生产需要很严格的无菌条件。到1941年秋季，皮奥里亚团队研制出一个类似搅拌洗衣机的旋转鼓，还配有一个注射器，可以不断地将无菌空气引入到发酵液中。这样的旋转鼓将成为未来五年工业制造青霉素的主要装置。



1941年9月，弗洛里结束了美国之行，回到了英国。但希特利没有和他一起回来——按照弗洛里的指示，他先留在了北方实验室，1941年12月他又去默克公司工作了6个月，直到1942年7月才回到英国。除了帮助青霉素项目取得了巨大进展外，希特利在美国的一年时间里收获了也失去了一份短暂的爱情。在北方实验室工作时，他和也是刚来不久的瑞士访问学者吉塔·布克哈德（Gita Burkhard）相识、相爱。这段浪漫随着吉塔于41年9月返回瑞士而结束。同许多战乱中浮萍漂泊的恋情一样，他们一旦分开便再无相见之日。

美国现代制药工业的诞生

OSRD的CMR负责人、弗洛里的朋友里查兹意识到青霉素对美国的重要性。1941年12月7日发生的日本袭击珍珠港事件又增加了生产青霉素的迫切性。生产几公斤的青霉素是不够的，美国必须探索在战斗中抗感染的各种可能手段，准备的青霉素越多越好。里查兹开始推动了备战的国家机器，并建立政府-企业联盟共同解决青霉素问题。对美国更为有利的是，由于英国医学研究委员会和洛克菲勒基金会的反对，牛津团队没有对青霉素申请专利保护。青霉素的开发权和生产技术的知识产权开始被OSRD，美国制药公司和农业部控制。

美国政府需要招募合格的、足够多的美国公司来提高青霉素产量。1943年，政府从申请的175家公司中选择了17个，其中有现在大家都熟知的名字：默克，施贵宝、辉瑞、礼来、雅培和瑞士制药公司罗氏在新泽西州的子公司。每个公司都被承诺可以免费获得关于青霉素发酵的所有信息，并可以独立拥有自己在项目里产生的任何新技术的知识产权。就这样，美国与化工、制药有关的公司被分为两个阵营：青霉素联盟圈里的和圈外的。

这些圈里的公司当时并不能算真正的制药公司：默克的主要产品是维生素，施贵宝以外科手术用的麻醉剂而闻名，而辉瑞最赚钱的产品是柠檬酸。但入选青霉素项目改变了他们的未来，并给他们带来了大量的实惠。仅在1943年，CMR就批准了对青霉素进行研究的总计超过270万美元的54份合同，并同意为生产商每百万单位的青霉素支付200美元。此外，由战争生产委员会批准，制药公司耗资近2300万美元建了16家新的青霉素工厂。作为鼓励，政府允许像默克和辉瑞这样的公司在记账时把他们的投资贬值期定为五年，以获得优惠的税收减免。战争生产委员会还花费了将近800万美元的联邦资金建了6家青霉素工厂。这些工厂在战争结束后被低价出售给私营企业。


►1944年8月14日Life杂志上刊登的青霉素生产的广告


青霉素联盟给制药行业带来了巨大的变化。在1929年左右，药物开发和制造业在美国利润最高的行业里只能排第16名，到1944年它跃居为最赚钱的。这种领先地位将持续近二十年。在青霉素联盟之前，这个行业是分散的，由数百家公司组成，没有一家拥有超过3％的全国市场。1944年，20家左右的公司成为行业的领头者，他们的产品总计占所有药物市场的80％，而该市场已增长了十倍。这20名获胜企业与其他公司的区别是，他们是圈里的，拥有青霉素合同。每个获得OSRD生产合同的公司都很快超过了其同行。从经济角度而言，一份合同相当于"增加300名研究人员或1000万美元的利润"。这相当于把行业的其他竞争者按着不让动弹，而让圈里的企业先领跑二十年。

1942年，在丘吉尔的督促下，英国制药公司也加入了青霉素扩大化生产。1943年，英国的青霉素产量和美国差不多，但到了1944年，英国的总产量只有美国的四十分之一。

后续科研 化学结构

弗洛里很早就意识到，只有破解青霉素的化学结构，才有可能弄清它的抗菌机理，才有可能进一步改进它的结构和疗效，才会充分发挥它在治疗方面或科学突破的最大潜力。从1941年起，钱恩和亚伯拉罕继续尝试破解青霉素的化学结构。他们不断提纯青霉素，并试图拿到它的结晶。

1942年，牛津大学的化学晶体学实验室的多萝西•霍奇金（Dorothy Hodgkin）开始与钱恩合作。她是X射线晶体衍射专家。钱恩和亚伯拉罕提供青霉素的晶体，她来分析。这种合作持续了3年。1945年，霍奇金终于解出了青霉素的化学结构。1964年，霍奇金凭借破译维生素B12的结构而获得诺贝尔化学奖。迄今她仍然是英国唯一的获得诺贝尔奖的女科学家。（霍奇金的故事很多很精彩。她热爱中国，曾多次访问中国。英国前首相撒切尔夫人是她的学生。她灿烂的一生需要我们仔细研读。）






诺贝尔奖

在青霉素开发的过程中，弗洛里团队不是一个完美的团队。团队主要成员来自三个不同的国家，虽然性格不合，但才能高度互补。弗洛里虽然有很多瑕疵，但他是一个承前启后的关键人物，也是一个成功的领导。他知道雇人就雇最强的，即使自己不喜欢对方。他有远见——他意识到要想大规模生产青霉素，美国是最合适的地方。他有网络——他依靠几个朋友和熟人使他和希特利的美国之行取得最大效果。

弗莱明、弗洛里、钱恩、希特利这些科学上的巨匠在生活中也是普普通通的人。他们也有喜怒哀乐。他们也会受欲望、虚荣心和恐惧所支配。当后人们仰望着他们立起的丰碑时，很少有人会知道他们曾经的焦虑和挣扎。

硝烟散尽，尘埃落定。1945年9月2日，第二次世界大战结束。同年12月，弗洛里、弗莱明和钱恩因为青霉素而被授予诺贝尔生理或医学奖。而做出巨大贡献的希特利无缘诺贝尔奖，不能不说是一种遗憾。他是青霉素背后的无名英雄。

1945年12月10日，在二战结束后的第99天，在斯德哥尔摩举行的诺贝尔奖晚宴上，诺贝尔医学院生物化学系主任Theorell教授向三位获奖者致词说："这一成果需要多年的辛勤工作，准确的直觉，深刻而广泛的知识，密切的团队合作和一些运气。在历史上最大的这场战争中，你们把青霉素奉献给全人类。但青霉素的用途只与和平有关。它连一只小鼠都伤害不了，却能治愈一个人。"

弗洛里从瑞士领奖回来，带了一套蓝色的葡萄酒杯送给希特利。希特利把它们摆放在橱柜里，但从来没有用过。他偶尔会拿出来看看——他喜欢这些酒杯的颜色。数年以后，有几个酒杯摔碎了，他也丝毫不介意。他早已看淡世间沧桑。生活还要前行，科学依然继续。

结语 青霉素在德国

到二战结束，青霉素一直掌握在盟国手里。德国在二战期间未能开发、使用青霉素令人费解，但我们推断可能有以下几个原因：1）德国虽然在化工上处于领先的地位，但大部分化工资源被用来生产别的军需品: 橡胶和汽油。2）德国制药企业的强项是化工合成, 在发酵生产方面并不占优势。德国科学家也因为磺胺药的成功而轻视青霉素。他们认为青霉素的化学结构不清楚，只能用"原始"的发酵方法生产，是科学的倒退。3）等德国人开始重视青霉素时，已经太晚了。到1945年，德国每月仅生产30克青霉素，只够治疗50名左右病人。在二战末期, 德国仅有的生产青霉素的厂房也被盟军轰炸殆尽。

青霉素的影响和意义

青霉素的成功开启了抗生素的黄金时代。1943年，还在读博士的艾伯特•斯卡兹（Albert Schatz）在美国发现了链霉素。1945年，意大利药理学家朱塞贝•布罗楚（Giuseppe Brotzu）发现了和青霉素机理类似的头孢菌素。在随后的两年里，广谱抗生素四环素和氯霉素被发现并应用到临床上。50年代又目睹了红霉素、甲氧西林的开发和使用。

磺胺药、青霉素和其它后续的抗生素使人类第一次可以治愈由细菌感染的疾病。人们的平均寿命大幅提高。仅以美国为例，从1938年到1956年，儿童疾病的死亡率下降了90％以上，人口平均寿命增加了十年以上。人口学家把这段时期称为"死亡率转变的重大拐点"。青霉素和其它抗生素创造了"现代医学奇迹的奇迹"。

青霉素的研发过程几乎成为现代医药研发过程的模板：生物现象的观察、体外实验、动物实验、人的安全性实验、扩大化生产、临床实验……和青霉素历史不同的是, 在当代药物研发过程中，弄清化合物的分子结构一定要先完成。

青霉素的独特之处在于它是通过发酵过程生产的小分子药。而这个发酵过程也成为如今生物蛋白药的生产流程的模板。现各大药厂广泛使用的上游过程（细胞株的选择和优化、细胞培养和收集）和下游过程（细胞分离或裂解、药物浓缩和提纯）中的很多概念和技术都来源于青霉素的发酵过程。

青霉素和抗生素黄金年代也改变了医生这个职业。在20世纪30年代，美国医生的组成很杂，混有很多非正规治疗师。因为在当时的历史条件下，医学院培训出来的医生和其它流派的行医者相比并不具优势——他们在病菌感染疾病面前都一筹莫展。他们那时的主要职责不是治愈，而是安慰。但抗生素改变了一切。从磺胺、青霉素开始，更多更强大的药物的出现，使得医疗行业需要更加集中的控制和监督。医生增加了处方权——他们有权决定哪个患者用什么药。越来越多的新药被认为药性太强，副作用太大或者太容易被滥用而不能直接销售给消费者。医生成为这些药物的看门人。这些更有影响力的医生以新的方式接受培训：医学院校日益重视建立在最新，最"科学"的研究基础上的分子生物学，生理学，微生物学和药理学等课程。没有掌握新方法的医师逐渐被边缘化。

后抗生素时代

日月如梭，光阴荏苒。时间到了21世纪，抗生素抗性成为威胁人类生存的最大危机之一。细菌繁殖快，突变也快，而且它们之间可以交换对生长有利的基因。从这点来说，出现对任何抗生素产生抗性的病菌只是早晚的事。但抗生素的滥用，尤其是在农业和养殖业中的大规模使用，加速了这一过程。而对我们更为不利的是，今天新开发的抗生素寥寥无几。由于经济的原因，各大制药公司没有足够的动力去开发新的抗生素。开发任何新药都耗资耗时，但抗生素上市后，或由于开处方时的严格限制而销量受到影响，或由于抗性病菌的出现和蔓延而很快失去使用价值。没有国家的政策支持，药厂连研发的成本都收不回来。


►自2016年以来，第一个已知的广泛耐药性伤寒疫情正在巴基斯坦蔓延。2018年2月，一个得了伤寒的婴儿在巴基斯坦的一家医院里接受治疗。


如果任由抗生素抗性的继续恶化，人类很有可能进入后抗生素时代，在一百年后再次对病菌感染无能为力。我们有可能又回到了文章开头那副漫画里的时代。我们绝不希望看到，弗莱明、弗洛里、钱恩、希特利和霍奇金等人用汗水和才智换来的成果付之东流。群星闪耀的青霉素时代不应该只是数万年来人类在微生物统治下奋起反抗的昙花一现。



本页刊发内容未经书面许可禁止转载及使用，公众号、报刊等转载请联系授权: Rebecca.du@lavfund.com

参考资料

1. Miracle Cure: The Creation of Antibiotics and the Birth of Modern Medicine William Rosen Viking (2017)

2. The Demon under the Microscope: From Battlefield Hospitals to Nazi Labs, One Doctor's Heroic Search for the World's First Miracle Drug. Thomas Hager. Three Rivers Press (2006)

3. The Mold in Dr. Florey's Coat: The Story of the Penicillin Miracle Eric Lax Henry Holt and Co. (2004)

4. wikipedia.org/

5. Imaging the Post-Antibiotics Future Maryn McKenna 11/20/2013 medium.com/@fernnews/im

6. 'We're Out of Options': Doctors Battle Drug-Resistant Typhoid Outbreak Emily Baumgaertner The New York Times 04/13/2018

7. nobelprize.org/nobel_pr

制版编辑：黄玉莹 |

本页刊发内容未经书面许可禁止转载及使用

公众号、报刊等转载请联系授权

copyright@zhishifenzi.com

商务合作请联系

business@zhishifenzi.com

知识分子为更好的智趣生活 ID：The-Intellectual



来源：知乎 www.zhihu.com
作者：知识分子

【知乎日报】千万用户的选择，做朋友圈里的新鲜事分享大牛。 点击下载
时间： 没有评论:

人物丨摇摇晃晃的跑者 与命运对抗的勇士

哪有什么限制，让那些质疑的声音随风去吧。——贾斯汀

贾斯汀（Justin Gallegos）是俄勒冈大学的大二学生，走在街上，看起来和别的学生并没有太大区别。

4月底，贾斯汀完成了尤金市半程马拉松，用时2小时3分钟49秒。这个成绩看起来平平无奇，没啥亮点，但如果我告诉你，他是一个脑瘫患者呢？

他参加此次比赛的目标是跑进2小时，这也是Nike的Breaking2计划的延伸，在比赛的后面几公里，他出现了严重的腿脚抽筋，本来就艰难的步伐变得更加沉重。在短暂的恢复后，他又跑了起来，大家都为他加油助威，当他最后冲过终点线时，和工作人员紧紧的拥抱在一起，眼里泛着泪花……

这是他的第一场半程马拉松，也是他参加的最长距离比赛，他在ins上更新的动态表达了他那一刻的心情：

"虽然没能跑进两小时，但我仍然很高兴，毕竟这是我的第一个半程马拉松！感谢我的后援团，尤其是配速员，他们都很棒。我参加这次比赛不仅想创造一个记录，而且想向每个人证明，未来有无限可能，遇到挑战时，不要给自己设限，限制我们的不是身体，而是思想"。

比赛后，肯尼亚跑者基普乔格（Eliud Kipchoge，破2计划实验时全马跑了2小时25秒的记录，被认为是最有希望跑进2小时的跑者）也发布ins表示祝贺。

幼儿园才学会走路

2015年，余秀华凭借《穿过大半个中国去睡你》爆红网络，诗歌走红的背后也引出了人们对脑瘫患者这一群体的关注。

总体来说，脑瘫是一种影响肌肉协调和身体运动的神经性疾病，每个患者的严重程度不一样。贾斯汀的症状是言语障碍、缺乏肌肉控制，这导致了他说话困难，走路总会跌倒。他2岁开始学走路，但是直到上幼儿园才能勉强走路。

"在高中之前，我并没有现在这么强壮，也不像现在那样活跃和喜欢社交，我很高兴跑步能带给我这些改变"。——贾斯汀

贾斯汀的跑步故事要从高中说起。他原本计划加入橄榄球队，不过他的父亲建议他去尝试下越野跑，谈及为何选越野跑，父亲布伦特如此说："我不喜欢劝阻他，也不会打击他，告诉他他做不到一些事情，其实让他选择越野跑，是因为我觉得橄榄球容易受伤"。

布伦特告诉跑步教练，贾斯汀在跑步机上做了很多训练，进了跑步俱乐部以后也会努力训练，可以跑5公里。就这样，贾斯汀开始了他的跑步生涯。

一次次摔倒，又一次次站起来

"在跑步俱乐部训练的第一周，贾斯汀跌倒了很多次，我甚至怀疑他是否应该继续跑步。他的膝盖和手肘摔的都是血，全是擦伤和淤青。不过他从来没有放弃，也从不会说，'我需要休息一下'、'我不想跑了'这样的话。虽然他在刚开始摔倒时会沮丧，跑最后一名会不开心，但他总能很快的调整心态，及时振作起来。跌倒了，就站起来继续跑，再跌倒，就再站起来。"，贾斯汀的父亲布伦特如此说到。

对于贾斯汀来说，每一步都是挣扎着前进，不协调的动作、艰难的步伐，同样的距离，他比常人要付出更多的努力，但他所迈出的每一步都那么有力量，每一步都是成长。

跑步没有捷径，只有努力训练才有可能取得提升，他必须适应新的行动方式和训练内容，尽管会经常跌倒，但是没有什么比通过努力训练赢得教练和队友的接纳更让他开心的事情了。

"跑步可以让我不断提升自己的运动能力。过去我也经常摔倒，现在虽然我比队友摔倒的次数多，但是通过训练我已经比以前好很多了，摔倒的次数越来越少。我感觉我正在变得更加强壮，而且这些训练也会有助于我更好的走路。"——贾斯汀

刷PB：不断突破自己的极限

在刚开始跑5公里的时候，贾斯汀的成绩是30分钟，他给自己定的目标是在比赛时可以快35秒，第一次比赛他就做到了，后来这一个人记录一直被推进，高二时已经可以在23:58秒以内完成了，天知道这对他来说有多难。

贾斯汀的1600米可以跑8分50秒，经过一段时间的训练，他给自己设立了跑进8分钟的目标。在一场1600米的比赛中，贾斯汀跑了7分54秒，实现了目标，而比赛当天的场景也让队友印象深刻："就在他快要完成的时候，观众里的孩子们都在跑道旁边来回奔跑，为他加油"。

对于教练詹姆斯来说，那些跑出很好成绩的学生会让自己感到高兴和骄傲，但是贾斯汀跑出7分54秒的结果也同样重要，而且这个成绩具有很强的感染力。

后来，贾斯汀又把这一目标提升到跑进7分半。教练詹姆斯说，"最后，他跑了7分14秒，我认为他会更快，有可能跑进6分30秒"。

灵感和激励的化身

作为跑步教练，詹姆斯喜欢告诉学生，跑步就像一场修行："如果你能够战胜内心的恐惧，出现困难时勇敢面对，跌倒或者发挥不好时能够快速振作起来，就会形成一种力量，受用无穷"。

作为校队的金牌教练，詹姆斯认为在激励队员方面，贾斯汀比他做的更多。

因为身体不协调，即使詹姆斯以最快的速度跑，也无法与队友或大部分跑者竞争，但他总能完成比赛。这种不断通过努力所带来的提升，大家是有目共睹的，这便是最好的言传身教，可以说，贾斯汀已经化身为灵感和激励的源头，他在的地方，总能带给大家不一样的震撼。

詹姆斯说，"他会在队友面前分享自己的训练经历，以及出现困难时自己是如何应对的，这些分享总能很好的激励队友。而且得到的回应比我还多，队员们都很清楚他经历过什么，因为他们正是看着贾斯汀一步步摔倒、站起来的，他们看得到贾斯汀的努力和坚持"。

每一次训练，贾斯汀都会尽全力。他总是早早的到达训练场，热身、认真的做每一个动作，为了完成训练目标，他需要作出比队友更多的努力，这些事情大家都有目共睹。

每次比赛的时候，他的队友、教练、朋友，甚至是共同参赛的跑者也会在终点线为他加油助威。

贾斯汀总有一种神奇的力量，通过跑步，将很多人联系在一起，大家总能在这里找到共鸣，找到奔跑的理由，找到坚持的动力。

梦想去参加残奥会

在高中三年里，贾斯汀的跑步成绩稳步提升，在800米、1600米、3200米项目中都取得了不错的成绩。毕业后，他想继续跑步，因为跑步已经为他带来了太多改变，成了他生活的一部分。

俄勒冈大学是北美著名的体育名校（Nike的创始人也毕业于此），以橄榄球和田径著称，这正是贾斯汀所梦想的地方。

他的好朋友卢克为他拍摄了一部5分钟的纪录片来作为面试材料：《没有这样的残疾：脑瘫跑者的故事》（No Such Thing As A Disability: The story of a runner with cerebral palsy）

《这不是残疾：脑瘫跑者的故事》

贾斯汀希望自己可以成为真正的运动员，做到那些人们认为他做不到的事情，而这也是他一直努力奔跑的一个原因。他希望去俄勒冈大学研究人体生理学，这样便可以成为教练，和其他残疾运动员一起工作。俄勒冈有一支很优秀的跑步俱乐部，贾斯汀希望可以和他们一起训练，以后有机会去参加残奥会。

如愿以偿，贾斯汀顺利被俄勒冈大学录取，为了支付高昂的学费，他还发起了一项"Go Fund Me"运动来为自己筹集大学费用，同时，他也会去别的地方通过演讲的方式来鼓舞跑者。

通过演讲和分享会，不光是跑友，普通大众也慢慢知道了他的故事，而这些故事所蕴含的能量也随着他的故事传递给了更多的人。

新的起点

在俄勒冈，贾斯汀做的第一件事就是申请加入跑步俱乐部，在试用期，他几乎每天都会去训练，而俱乐部并没有要求队员天天训练。提前出现在训练场、认真的完成每一组训练，就跟当初刚跑步时一模一样。

俱乐部的高年级学生威拉德这样评价贾斯汀："你可以明显看到他对跑步和俱乐部的热爱，他对跑步的热爱，融入在生活的点点滴滴，通过他的跑步方式、行为方式，以及与人交往的方式传达给每一个人，贾斯汀是一个非常真诚的人，他能加入俱乐部真的很棒，带给了我们很多东西，可以很好的激励大家"。

俱乐部的主教练大卫也对贾斯汀评价颇高："他投入训练的努力激励着每个人，大家都喜欢贾斯汀，会为他着想"。

现在贾斯汀已经不怎么跌倒了，他参加了加州举办的田径锦标赛残奥会，虽然他更喜欢1600米以上距离的比赛，但这次比赛的最长距离是400米，不过他还是参加了这次比赛，并且获得了第一名 。

他的梦想是能够在残奥会上代表美国队，参加1500米的比赛。

现在回过头来看视频中贾斯汀跑步的身姿，就像少年阿甘，虽然动作显得有些不协调，但最终他必将摆脱束缚自己的枷锁，跑出属于自己的人生。

限制自己的从来都不是身体，而是思想，让那些质疑的声音随风去吧。——贾斯汀



来源：知乎 www.zhihu.com
作者：爱燃烧

【知乎日报】千万用户的选择，做朋友圈里的新鲜事分享大牛。 点击下载
时间： 没有评论:

健身新人选择健身房的四点考虑

今天照顾一下新手，讲讲新人如何选择健身房的问题。



在我刚开始去健身房的2001年，即便对新人来说，选择健身房也并不困难——整个城市就那么几家健身房，你根本没得选。而在2018年的今天，健身房的数量多到令人眼花缭乱，街上到处是散发传单拉人的会籍顾问，这时候选择健身房就成为一个大问题了——究竟什么样的健身房，才最适合你的需要呢？



在这个问题上，刚开始健身的新人和有长期健身经验的老手是不一样的。这是因为他们需要考虑的因素完全不同：



有长期健身经验的老手——他们已经有了明确的健身目的，也知道什么样的健身房能够提供自己所需要的训练条件，而且在坚持长期健身之后，运动习惯早已根深蒂固，所以他们更看重健身房的器械条件，至于距离远近、洗澡条件等等，相对来说都处在比较次要的地位。



刚开始健身的新人——他们对健身还所知甚少，健身目的往往尚不明确，甚至存在一些不合理的要求（例如部分女生盲目追求瘦，喜欢麻杆一样的胳膊腿），自然也不清楚什么样的健身房能够提供自己所需的训练条件。另一方面，他们刚开始健身，运动习惯尚未养成，很容易因为自身的惰性而在遇到困难时打退堂鼓，甚至放弃健身。



有鉴于此，我建议刚开始健身的新人在选择健身房时，要把"有利于让自己坚持下去"作为第一考量，重点考察以下四个与此有关的因素：



距离——现代城市的生活模式决定了人们每天都要在上下班路上耗费很多时间，而漫长的路程往往让人身心疲惫，做什么事都打不起精神。在此基础上，如果去健身房的路途也十分遥远，那就很容易让人产生厌倦心理，丧失运动的兴趣和动力。所以刚开始健身时，最好选择离住处较近的健身房，这样不容易因为路途遥远而打退堂鼓，放弃健身。


（如前所述，长期健身的老手已经养成了运动的习惯，不会因为距离远一点就放弃。例如我有个小伙伴上大学前就健身多年，到北京读大学后每周三四次骑车从北师大跑到东单的青年会健身房去锻炼。各位可以看看地图上这两地距离有多远，骑车又需要多久）



环境——这主要包括两方面，一是健身房的装修、灯光、音乐等是否令你感到舒适愉悦，有些健身房喜欢用耀眼的灯光或强劲的音乐来带动会员的情绪，而这可能让一部分好静喜暗的人感到不适。二是健身房的通风、温度等，如果通风和温度做得不好，夏天闷热难耐，冬天湿冷难耐，就很容易成为新人"说服自己不去健身"的理由。


（对应地，有长期健身经验的老手更看重健身房提供的训练条件能否满足自己的需要，对环境因素相对不太在乎。例如我以前去过一家铁馆，每逢下雨天房顶都有渗漏的雨水滴落，冬天四面透风冷如冰窟，但我更看重这里的杠铃杆是举重队淘汰下来的，弹性好强度高重量足，所以在那里练了很多年）



价格——对于新人来说，价格是把双刃剑：健身卡的费用很高，会让一部分人望而却步，止步于健身房门外，但一旦办了卡，便很容易产生"这钱不能白花"的心理，并以此为支撑度过最难坚持下去的健身初期。反之，便宜的健身卡会让新人更容易跨进健身房的门槛，但也更容易在坚持不下去的时候说服自己"反正没花几个钱，就当买教训了"。所以在挑选健身房之前，建议先想一想自己更可能做出上面四种选择中的哪一种，然后再考察各家健身房的价格，做出决定。


（对应地，长期健身的老手并不需要靠价格等外界因素来敦促自己坚持健身，另一方面，因为健身对他们来说已是一种基本需要，所以对价格的敏感度也较低）



服务——健身房工作人员的服务态度也是新人需要考量的因素之一，这一点与其他服务行业大同小异，因此就不多说了。只针对健身房的特殊性专门提一句：如果接待你的工作人员（会籍顾问或教练都有可能）跟你谈了没几句就开始诱导你不仅要办卡还要买私教，那么这家健身房对员工施加的业绩压力很可能非常大，而压力大容易让人心情不悦，进而影响到工作人员对你的态度，这样就让你又多了一个不去健身的理由。


（对应地，长期健身的老手一般不会被纠缠买私教……健身房往往更怕他们去教别人，抢了自己的生意）



以上就是我对刚开始健身的新人如何选择健身房的四点建议。至于健身房的器械问题，在这个阶段暂时还不必列入考量，其具体原因将在下一篇更新中阐述。


（本文同时也发表在我的个人公众号：不仅是健身。欢迎各位关注）



来源：知乎 www.zhihu.com
作者：kmlover

【知乎日报】千万用户的选择，做朋友圈里的新鲜事分享大牛。 点击下载
时间： 没有评论:

你有没有一种"黑色生命力"? | 只有少数人，经历越多困境越强

今年KY小姐姐们决心要有更多的烟火气，开始努力刷综艺（事业心烟火气）。结果被歌手里的张韶涵击中了。《阿刁》是今年听过最感人的流行歌，今天还在单曲循环。

节目中张韶涵谈到歌里的女孩让她联想到自己，于是特意去搜了搜她的故事，觉得张韶涵能唱好这首歌是有原因的：

据媒体报道，小时候因为爸爸身体不好，常年无法工作，张韶涵就边上学边打工。后来她成为当红的偶像剧女主，她的歌也广为传唱（本科校长曾表演唱过她的"隐形的翅膀"）。后来她与母亲"反目成仇"，在她治疗心脏病期间，母亲拿走了她所有的积蓄，并公开指证她吸毒、酗酒，她的事业也一落千丈。

直到她在歌手中用《阿刁》一鸣惊人，人们看到这些年的时间和苦难在她身上的结晶：一种很纯粹、很本真的力量。



这让我想到，明尼苏达大学发展心理学家、临床医师Norman Garmezy，在他四十余年的研究中，见了数以千计的孩子。其中有一个男孩，得到了他持续多年的关注。

他认识这个男孩时，他9岁，有一个酗酒的母亲，没有父亲，吃不饱饭。尽管如此，长大过程中，男孩始终在学业、人际、心理健康方面都表现良好。

这个男孩属于一群特别的孩子。——在很多年的时间里，Garmezy寻找那些处在糟糕的处境中，有很大概率成为问题少年，但实际却成长得令人骄傲的孩子。Garmezy说，他们"尽管经历过异常困难的处境，却不断走向成功、不断获得超越大多数人的优秀"。

今天KY想跟大家聊聊，张韶涵和这些孩子身上具有的这种力量——经历过创伤而最终度过的人身上会表现出来这种力量，一种穿越黑暗，在挣扎与恐惧之间迸发出来的巨大能量。为了方便大家理解，我们把它叫做"黑色生命力"。



每个人身上都有一种生命力，支撑着我们迎接每一天的开始。但"黑色生命力"不同，我们用它特指那些，经受过巨大的压力、逆境和/或创伤，并渡过、幸存（survive）下来的人，最终展现出来的一种力量。

它主要包含三个层面：

1.情绪能力

这种情绪的能力包括两个层面：

  • 一个层面是情绪的广度，也就是说，这些经历过创伤的人，除了日常的喜怒哀乐之外，他们体验过极端负面的情绪，因此比一般人拥有更复杂、更广泛的情绪体验；他们能感受和体会的情绪是更多样的、范围更宽广的。


  • 另一个层面是情绪的深度——相应的情绪理解能力与处理能力。在经历创伤而幸存的过程里，他们曾与自己极端的负面情绪做过正面交锋。在这个过程中，学会了如何与自己悲痛、失望等负面情绪同在，虽然负面情绪总是令人不快，但他们学会了不在负面情绪前手足无措。


他们熟悉痛苦，虽然一切仍然不会变得容易，但他们的确比没有经历过重大负面经历的人更懂得如何处理痛苦。

除此之外，经历过创伤的人也更能共情他人的情绪。Arous等人（2016）对经历过童年创伤的人（遭受性虐待、情感忽视等）的研究发现，痛苦的人比快乐的人共情能力更强，更能真切地对他人的情绪感同身受。这可能是这些自己曾深刻体会过痛苦的人，对他人痛苦的一种"条件反射式"的敏感。





2.对复杂的认知和理解力

经历过创伤的人，有一种对复杂现实的认知和理解能力。他们曾经经历过极端的状况，对真实世界的复杂有着高于一般人的认知，比如"本该是世界上最疼爱我的人，却做出了伤害我的事"，"本该相互坦诚的人，却相互欺瞒"等等。因此他们相对更少会对复杂感到意外。

第一次面对复杂、难以理解、逻辑上不一致的现实，总是最难的。

可以说，他们在穿过创伤的过程中，承受了这种不一致。他们也曾感到绝望或愤怒，但最终他们的生命消化了这种不一致和它所承载的情绪，形成了他们对复杂的识别与了解，他们也能以此为世界的复杂做好准备。

同时，这也让他们更容易从不同的视角看待真实。他们可能比一般人更清楚地了解：世界上没有黑白分明的"好"、"坏"。实证研究也的确发现，经历过童年创伤的人，换位思考的能力更强——更能从不同人的角度出发去思考问题（Arous, et al., 2016）。有时候这对他们来说甚至不是一种意愿：他们只是更能够看见，非常自然地看见。因为曾经极端的痛苦曾经逼迫他们不得不去揣摩他人，非常困难地去解读伤害自己的人和事件——他们在这个过程中得到了锻炼。

3.一种得以应对世事变迁的人生哲学

经历过创伤的人还会获得一种人生哲学，又被心理学家Tedeschi（2004）称为"智慧"（wisdom），它包含4个层面，自我、他人、世界观，以及行动准则。

首先，个体会变得更加"自我依靠"。在度过创伤的日子里，他们体会到了自己比想象中更强大，更相信自己是可以依靠的，这种自我效能感与价值感的提升会成为支撑Ta度过人生中更多坎坷与挑战的力量。

同时，他们也会变得更珍惜关系。在他们度过创伤的日子里，不论是因为曾经寻求过或获得过的他人帮助与支持，还是曾经失去过重要的人，都让他们更懂得感恩，珍惜人与人之间的关系与链接。张韶涵也坦言，人生的低谷期让她更加珍惜身边真正爱她的朋友和家人。


另外，经历过创伤，也让他们不再一味对世界抱有美好幻想，而是对人生的艰难与坎坷有了更多的心理准备。尽管这在外人看来，或许有些悲观，但却令他们拥有了一种面对世事变迁的平常心，我还看到张韶涵在一个访谈里说，"直到现在我才了解，原来人生就是这么无常"。她真的是被生活的苦赋予了深度的一个明星。

拥有黑色生命力的人，对风险的"忍受"能力也会变得更高。也正因为如此，相较而言，在这些拥有黑色生命力的人生中，也有更多的机会/可能发生一些不寻常的事。






尽管，黑色生命力"属于"经历过创伤的人，但并不是只要经历过创伤，人就可以获得这种黑色生命力。

当创伤发生，人们会遇到三个层面的挑战，在任何一个挑战上失败，黑色生命力都不会发生。

  • 对情绪管理的挑战：创伤发生后，人会有一些应激性的极端负面情绪，会经历剧烈的情绪波动；


  • 对生活叙事的挑战：当面对创伤的时候，人们也需要给自己一个合理的解释——"为什么是我"，"我遭遇的为什么是这些"，"父母为什么这样对我等等"，人们原有的理解自己人生的方式会受到挑战，需要一套合理的说辞，一种新的讲述自己人生故事的方式（即新的生活叙事）；


  • 对人生图示与信念的挑战：这指的是，创伤会挑战我们对世界和人性的基本认知，会让我们怀疑人生（比如，父母不应该就是对孩子关心呵护的吗？他/她怎么忍心下这么重的手打我？）。


有些人会长时间地想要压抑心中内疚、自责、沮丧、羞耻、自我怀疑、绝望等情绪，也放任自己反复陷入"反刍思考"之中（rumination），比如他们会不断地去想"是不是我当时做错了什么，父母才会这样暴力对待我？"，"是不是如果我努力变得更优秀，他们就会对我更好？"等等，使得自己长久地活在过去的创伤之中。

而另一些人度过创伤的过程则是：

1.接纳自己那些极端负面情绪的存在

比起压抑情绪，这些人选择承认自己在面对创伤时所感受到的种种情绪，允许它们存在。正如张韶涵在采访中所说，"如果说不痛，肯定是假的"。她选择去承认和面对这些情绪，找到应对的方法（比如找到她朋友和弟弟妹妹的陪伴和支持）。

2.积极的认知重评（positive cognitive reappraisal）

当情绪被允许存在之后，他们开始展开一种叫做 "认知重评"的过程，系统地分析这件事对自身的影响。他们会在不是自欺欺人的前提下，努力倾向于以更积极的方式去叙述创伤，比如更着重去讲述经历了这件事，自己获得了什么。但不会否认这件事本身的悲剧性。

认知上的改变，会让人们对创伤的情绪感受发生积极的改变（Troy et al.,2010），比如，认为自己最终经受住了而感到"欣慰"，因为接受了这就是一种"不幸运"而停止自责。心理学家指出，认知重评是"控制和管理艰难情境"最有效的策略（Castro, et al., 2016）。

3.有意义的反刍（deliberate rumination）

他们也会进入对创伤的反刍思考，但不同的是，他们更加专注于"对问题解决、意义寻求的回忆与思考"之中（Martin & Tesser, 1996）。

也就是说，比起自责，他们会在反复思考的过程中，去看到自己曾为解决困难做出过哪些尝试，哪些是奏效的（可以被之后继续使用的）——这可以帮助他们为今后的人生挑战做好准备，也有利于他们积极地去理解创伤。

不同于其他人，Zoellner和Maercker（2006）发现，以这三个步骤经历创伤的这一类人，更有可能在尝试与创伤抗争的过程中幸存下来，并在这个过程中获得积极的成长——获得属于自己的黑色生命力。

正如前文所说，并不是所有人都会以同样的方式经历创伤，但为什么不同的人会以不同的方式经历创伤呢？

首先，这与先天因素有关，我们的基因影响着我们应对创伤和负面情绪的方式。

其次，在成长的过程中，一个人是否曾经在他人的身上见到过"黑色生命力"，也会影响Ta在面对创伤时的反应。这就是榜样的力量。

换句话说，黑色生命力，也是极具感染力的，它会给周围人带来面对创伤的勇气。

不仅如此，自身经验的积累，也对人们经历创伤的方式有影响。如果在早年经历的创伤中，我们曾经偶然尝试过"认知重评"，并感受到积极应对创伤的好处，我们就更可能在之后遭遇创伤时，以这样的方式尝试与创伤抗争。也可以说，黑色生命力，是一种可以持续累积的力量，是一种良性循环。






越来越多的研究发现，糟糕的经历本身并不决定一个人的未来。

发展心理学家Werner也曾经对698个孩子进行了长达32年的跟踪研究。在这个过程中她发现，那些经历过创伤与痛苦的孩子中，有一部分成长为了"有能力、自信和充满关爱"的人，并取得了学业、家庭和社会意义上的成功。

在对这群孩子人格特质的进一步研究中，Werner发现，这些孩子并没有什么特殊的天赋。重要的是，这些孩子远比一般人更相信：自己的未来更多是由自己掌控的。他们首先深知自己的不幸，承认自己的不幸，随后持续地与这些不幸抗争，并认真地活下去，最终在这个过程中获得了平静和力量。

是否遭遇创伤，任何人都无从选择。但我们的的确确可以选择度过它、穿越它去看到自己生命的另一种力量。

有人说，曾经经历过的创伤会形成一道伤疤。这可能是真的，但一道伤疤，同时也是一枚勋章。它提醒着你曾经有过的抗争、取得的胜利。

对于有些人，活着的感觉，像一座山峰连着一座山峰，一场战役连着一场战役。似乎比一般人更难，有时觉得看不到尽头和希望。但如果你停下来看看自己，你会发现这些攀登和战斗的过程，已经在你身上留下了"好的结果"。

拥有黑色生命力的你，将越来越在找到幸福的路上，变得不可（被命运）阻挡。

加油吧少年。
以上。






References:
Arous, A. et al., (2016). The associationbetween childhood trauma and empathy in patients with stable schizophrenia.European Psychiatry, 33, 114-289.
Castro, M. C., Martínez, M. A., &Abarca, X. F. (2016). Deliberate Rumination and Positive Reappraisal as SerialMediators Between Life Impact and Posttraumatic Growth in Victims of StateTerrorism in Chile (1973-1990). Journal of Interpersonal Violence, 1-17.
Martin, L. L., & Tesser, A. (1996).Clarifying our thoughts. Ruminative thought: Advances in social cognition, 9,189-209.
Tedeschi, R. G., & Calhoun, L. G.(2004). " Posttraumatic growth: Conceptual foundations and empiricalevidence". Psychological inquiry, 15(1), 1-18.
Troy, A.S., Wihelm, F.H., Shallcross, A.J.,& Mauss, I.B. (2010). Seeing the silver lining: Cognitive reappraisalability moderates the relationship between stress and depressive symptoms.Emotion, 10(6), 783-795.
Werner, E. E., & Smith, R.S. (1982). Vulnerablebut invincible: A longitudinal study of resilient children and youth. New York:McGraw Hill.
Zoellner, T., & Maercker, A. (2006).Posttraumatic growth in clinical psychology: A critical review and introductionof a two component model. Clinical psychology review, 26(5), 626-653.

KY作者/罗勒

编辑/KY主创们


想更有针对性地解决拖延症、提升自我管理能力，请关注KY心理课：【KnowYourself】KnowYourself, 宇宙中最酷的泛心理学社区，人人都能看懂，但只有一部分人才会喜欢。-跟谁学官网

想要了解更多的心理学专业文章，请关注：KnowYourself知乎专栏

点击查看过往高赞回答：

年轻人千万别碰哪些东西？

有哪些看似聪明，实则很傻的行为？

有哪些看似很傻，实则聪明的行为？

为什么有些人恋爱中感到不合适，就分手？

是不是文化程度越低的女孩，越把希望寄托于嫁人，而不是自己努力？

为什么一部分女性不喜欢生孩子？

有哪些细微但是高效有用的习惯？



来源：知乎 www.zhihu.com
作者：KnowYourself

【知乎日报】千万用户的选择，做朋友圈里的新鲜事分享大牛。 点击下载
时间： 没有评论:

这三个字，比“我爱你”更动听

壹心理主笔团 | 触角

——


520，521，五月红包鲜花礼物轰炸朋友圈，满屏都是恋爱的酸臭味。

哈哈，不是我泼冷水。

检验爱情的最佳场所，不是狂撒狗粮的朋友圈，而是在孤军奋战的产房里。

相信我，【生孩子】绝对是爱情关卡中的大boss。

顶着10级的剧烈疼痛，伤口不断拉开，凭着"一定要生下来"的执念和本能，不断坚持地用力，直到听见"哇"一声之后，才发现自己已经虚脱了。

但这一切，才刚刚开始。

在庆祝宝宝诞生的喜庆气氛中，其实有多达50%~80%的女性，都在一个人忍受着产后抑郁情绪的煎熬，常常莫名想哭、时不时焦虑抓狂。

更加让人心疼的是，有大概11%的新手妈妈，会患上产后抑郁症，被抑郁或烦躁的情绪淹没，甚至走向轻生。

但是，在宝宝诞生这样喜悦的氛围中，这些抑郁的情绪常常只能在新手妈妈心里秘而不宣地积累着，无法被家人所看见和理解。

在520这个日子中，或许最应该被爱又最容易被忽视的，就是这些为了爱情奋不顾身生下宝宝，却被产后抑郁困扰的妈妈们。

婚前多少个520，都不如产后的一句"我懂你"。



01

"带来了爱的结晶，却没了笑的力气"

产后抑郁症：沉重的爱的伤疤

产后抑郁症究竟是怎么一回事呢？

很多患上产后抑郁症的新手妈妈，会在产后6周内第1次发病，整天容易感到抑郁、悲伤、沮丧、哭泣、易激动、烦躁、内疚，严重时可能会出现幻觉或者自杀。

听起来非常沉重。

那英曾自曝生下第一胎后，患上了产后抑郁症。

在长达几个月里，不知道为什么每天都会哭，经常坐在床上一夜一夜失眠不睡觉，甚至怀疑送饭的保姆给自己下毒。

最后看了医生，才慢慢恢复过来。


怀孕时高兴着可以为爱带来结晶，为家庭带来新的生命，但为什么把宝宝生下来后，就抑郁了呢？

目前有以下这几个产后抑郁症的成因。


1. "不知道为什么我整天都很沮丧"

——产后体内的激素在作怪，身不由己

生孩子那么开心的事情，怎么就抑郁了呢？

这大概是所有产后抑郁症的新手妈妈最大的委屈吧。

像那英"莫名奇妙地哭"的行为，在"生孩子是喜事"的社会认知下无法得到理解，但却并非无理取闹：因为此时体内的激素们，正在急剧变化，在产后24小时内尤为剧烈。

例如其中的一种激素——胎盘类固醇：在临产前，它会大量释放，给准妈妈们带来了一个愉悦的心境，但在产后，它却急剧地减少了分泌。

这种变化，让新手妈妈们从快乐的云端，一下子地跳入了黑暗冰冷的崖底，抑郁和焦虑如潮水一般涌来，让新手妈妈们猝不及防，身不由己。

此外，雌激素、黄体酮、甲状腺激素等也是在孕晚期增加，但分娩后突然撤退，对新手妈妈一些更高级的脑活动有了影响——例如，难以理性、深度地思考问题。

同时，生宝宝本身就会让新手妈妈身体疲惫、情绪低落，从而影响到神经系统功能的进一步衰退，内分泌更加不稳定，进一步促进情绪低落。

如此恶性循环，让很多妈妈陷入抑郁，做出一些"反常"的行为：经常哭泣、烦躁爱吵架、一夜夜地失眠不睡觉。


2. "拖着疼痛的身体，却需要立刻适应新身份"

——巨大的心理压力vs脆弱的情感时期

刚刚经历了一次身体撕裂、神经紧绷、疼痛难熬的身心大战，很多妈妈都会在产后1个月出现暂时性的心理"退化"，行为变得更加孩子气，情感上也变得非常脆弱。

但接下来的事情却一件件侵袭过来，刻不容缓：

母亲角色切换、母亲责任的承担、笨手笨脚地照料宝宝......让她们没有喘息的空间，心理压力山大啊！

何洁也曾自曝自己患上了产后抑郁症，在身份转变的压力下，她说：

  • 我觉得自己就是一个完全没有用的人......
  • 一个被抛弃的人，除了喂奶没有其他用处……
  • 真的我都想自杀了.....



不知所措、焦虑、烦躁......这些负面情绪进一步影响着激素的分泌，一步步把她们推向了更深的抑郁情绪中。


3. "当丈夫说我矫情的那一刻，我绝望了"

——支持、关爱的缺乏，抑郁愈演愈烈

调查表明：缺乏家庭的支持与帮助，特别是来自丈夫和长辈的帮助，有可能引发产后抑郁症。

但支持的缺乏在现实中并不少见。

之前采访过一个产后抑郁的妈妈，她感叹到：生完孩子之后，你什么都不是，你只是一个孩子的妈妈而已！

  • 无论半夜几点，孩子一哭你就要起来喂奶，但身边的老公却睡得昏天暗地；
  • 为了奶水充足，无论婆婆煮的汤有多难喝，你都得闭着眼睛喝下去；
  • 除此之外，你还要轮流听七大姑八大姨那些过时的护理知识，连休息的时间都没有.....


没有人问你是否需要帮忙，没有人在孩子哭的时候帮忙抱一下，所有人都在让你履行好母亲的角色，却没有人在乎你累死累活的心情，感觉自己像是孤军奋战一样。

研究表明，良好的支持可以帮助新手妈妈提升自信，缓解压力，减轻负担，而产后存在抑郁情绪的产妇所获得的社会支持是匮乏的。

这种支持的匮乏，会让人在最身心疲惫的时候，感到无助，负面情绪增多，更加容易走向抑郁。


除了上面列举的3个之外，遗传因素、重大变故、产后并发症也可能会是产后抑郁症的原因之一。

但要注意的是，产后抑郁在一开始可能只是一种情绪。

但如果这些情绪没有得到关注和疏导，最后种种因素加强，可能会促发产后抑郁症，造成更加严重的后果。

那么作为她最亲近的另一半，应该如何让【为爱生娃】的她，能够减少精神上的折磨，得到疗愈呢？


02

她产后抑郁最需要你时，如何把520爱到实处？

刚生完宝宝，可能是一个女人生命中最需要爱的时刻。

在这个时候，作为她的另一半，你可能在昏天暗地睡着大觉、偷懒着不帮忙喂奶换尿布的过程中，默默地加深她的抑郁症状；

但你也可以选择用另外的方式，守护着她，履行那些曾在无数个520中许下的"我爱你"的承诺，把她从产后抑郁的边缘中拉回来。


1. "你是不是产后抑郁了？"

——关注"产后抑郁"，做她身心健康的保护伞

虽然几乎每10个新手妈妈，就会有5-8个会有产后抑郁的情绪，有1个会患上产后抑郁症，但由于"心理疾病"的羞耻性，很多新手妈妈甚至家人，都倾向于不去直面和重视，甚至处于认知空白的状态，因此可能会被误会成"矫情"或"丧气"。

演员秦海璐曾在节目中透露，她生完孩子后，就患上了产后抑郁症，每天就不停哭。老公还觉得是自己惹她哭的，就躲避着她，这样反而让她更难过了。


可见，缺乏对【产后抑郁】的认知，足矣把这个事情搞得更加糟糕。

那么作为她亲近的人，应该怎么关注到她是否有产后抑郁，而又应该怎么做呢？

产后6周是产后抑郁症的多发时期，在这段时间内，如果发现她有一些异常的情况，例如经常哭泣、莫名感到内疚、极易焦虑和烦躁等，需要给她提供更多的社会支持，以此缓解抑郁情绪。

社会支持一般分为3种，包括：

  • 情感支持：多陪陪她，亲亲她；
  • 信息支持：和她一起学习如何哺育孩子、科学地做好产后护理；
  • 评价支持：肯定她是个好妈妈，在她照料孩子的时候，多夸夸她.....


而如果发现她有一些轻生的念头，例如"我不如死了算了"等，需要及时重视，马上带她去看心理医生。

据调查，目前有80%的产后抑郁症患者未被发现并作出明确的诊断，因此提前预防产后抑郁情绪的加深，并早期识别产后抑郁症状，是奶爸们非常重要的任务。



2. "我在呢，我来吧！"

——不要让她孤军奋战

前面说过因为体内激素、身份的变化、责任的增多，可能会加深新手妈妈的抑郁情绪。

前面那个"半夜起来喂奶，老公在睡大觉"的新手妈妈，曾在某个喂奶的半夜，强撑着疲惫的身子，听着丈夫巨大的呼噜声，突然觉得日子太孤独、太痛苦了，巨大的绝望感涌向心头，精神一下子就崩溃了。

每一点每一滴的抑郁情绪，都可能会在每个疲惫的深夜慢慢累积，直到崩溃；但它原本也可以在决堤之前，在一个个爱的细节中被慢慢消解。

作为奶爸的你，可能每天只需要多留一个小时，就能让她不再孤军奋战：

  • 或是在下班之余带一带小宝宝，让她喘口气；
  • 或是准备饭菜、帮孩子换尿布；
  • 或是半夜醒来给她一个拥抱，陪她一起喂奶，让她不觉得孤单......


爱从不是平静日子中的一碗糖水，而是兵荒马乱中，仍然愿意递出的一只援手。

实在的行动支援，可以有效缓解新手妈妈的压力，避免抑郁情绪的进一步袭来。

3. "我懂你，谢谢你，我爱你"

——爱的表达，能给她很大的鼓励

最后，除了行动上的支持之外，奶爸们提供的心理支持，也可以很大程度上帮助新手妈妈们缓解压力，减少抑郁的发生哦~

若要想让她感受到你的情感支持，爱的表达很重要。

很多新手奶爸常常会在孩子诞生后手忙脚乱，只顾着帮忙，却从不知道表达，或者，不知道该怎么表达。

但其实，爱的语言并不难——有时候短短的三个字，就能让她感受到你的懂得、支持和爱。

更多有趣有用的心理知识，请关注公众号【心理公开课】。在焦虑时代，学点心理学，你会发现幸福也没那么难



来源：知乎 www.zhihu.com
作者：壹心理

【知乎日报】千万用户的选择，做朋友圈里的新鲜事分享大牛。 点击下载
时间： 没有评论:

读懂刑事判决书……的法律引用

之前曾有人建议我开live讲讲怎么读一份刑事判决书，但我觉得范围太广不好讲，比如光是这个法律引用部分（注意法律引用不是法律适用），灌起水来就能讲一小时，加上一堆事情忙也没时间去准备，live是懒得弄，不过还是按不同的部分写个专栏文章，给有兴趣的人看看。

刑事裁判文书中，可能人们最没兴趣读的部分就是"依照《中华人民共和国刑法》第XX条之规定，判决如下"这句话。也许与该案有关的检察官、律师还会注意一下法条是否错误，但是，除了写判决的法官和签发的审判长之外，几乎不会有其他人注意这法条的引用顺序是否正确。

不过，这真的是个技术活。

一、都能引用什么法律

1、基本的引用范围——法律、法律解释、行政法规、地方性法规、自治条例或单行条例、司法解释

作为裁判文书的判决法律依据，通常就只能引用上面这个范围里的法律。广义上的"法律"的范围比上面这个范围要大，但超出这范围的部分，就不能作为"依照XXXX之规定"的依照内容了。

另外在引用的时候，必须精确到 X条X款X项X目，而不能笼统地只写个第X条。如交通肇事罪有多个入罪标准，可能是一人重伤+无证，也可能是1人死亡，就必须明确写清楚具体入罪标准的条文。

2、需要引用的条文

凡是在判决主文中出现的内容，都必须有清晰的法律依据，即每个判项都能在判决主文处找到明确对应的条文。

  • 关于定罪的条文——

首先必须有刑法中的定罪条文，如盗窃罪必须要用刑法第264条；如果是"援引式"定罪，要同时引用援引的法条的被援引的法条，如保险公司的人以职务之便编造保险虚假理赔，构成职务侵占罪，要同时引用第183条和第271条。

其次是法律解释和司法解释中对罪状和犯罪构成要件作出的解释，如事业单位的人以国家机关工作人员身份实施的渎职犯罪要引用全国人大常委会《关于刑法第9章渎职罪主体适用问题的解释》；又如寻衅滋事罪要引用《寻衅滋事司法解释》第一条对"寻衅滋事"的定义。

再次是关于入罪标准的法条。刑法中的绝大多数条文都没给出明确的入罪标准，而是由其他司法解释性质的文件来规定，因此关于入罪的标准是必须引用的。如果有特殊情节导致入罪标准减半，还要引用相关的条文，如盗窃罪中，关于入罪标准 的法律依据是《盗窃司法解释》第1条，但是曾有盗窃前科会使入罪标准减半，就要同时引用《盗窃司法解释》第2条第1项。

  • 关于量刑的条文——

首先是关于量刑幅度的条文。虽然很多时候量刑幅度与犯罪是同一条，但也存在单独有量刑幅度的条文，典型例子就是贪污罪、受贿罪的量刑是单独一条：第383条。

其次是量刑档次（加重情节）的条文。刑法条文中规定的量刑档次一般都在罪名的条文中一起引用了，如抢劫数额巨大，可以直接用第263条第4项。需要另外专门引用的一般是在司法解释里面规定了加重情节或加重量刑档次的标准，如交通肇事罪，如果认定致2人死亡情节特别恶劣，就要引用《交通肇事司法解释》第4条第1项。

再次是与具体刑罚相关的条文。主刑如果是自由刑，一般不需要专门引用相关的总则条文；但如果是非监禁刑或者死刑，就需要引用相关条文了。另外附加刑也需要引用相应的总则条文。

第四是量刑情节。如自首、立功、从犯，或者非法拘禁中侮辱、殴打的法定从重情节，都要引用。

  • 其他需要引用的条文

首先，引用程序法的条文。如二审判决或裁定，需要引用刑事诉讼法关于二审的规定。无罪判决也需要引用刑诉法及解释中关于证据不足无罪或事实不构成犯罪的无罪条文。

其次，引用其他法律的条文。如刑附民，需要引用民法通则第36条，以及其他相关的民事法律与司法解释。

再次，对涉案财物的处理，要引用刑法第64条。

最后，是兜底条款的"其他"，防止有所遗漏。

但是其中有一些条文是"解释、说明"性质的，如61条规定的是"怎么量刑"，《最高院关于财产刑若干问题的规定》第2条规定的是"怎么判处罚金"，属于可引用可不引用的范围。从规范法律引用的角度来说，当然是引用了比较好，但是引用的话会导致法律引用这部分内容过于杂乱，那对于这种次要的条文也可以略去不引用。

3、千万不能作死之一：禁止引用的内容

如国际条约，即使是我国已经参与的，现在的观点仍然是不直接作为法律依据。至今为止也没有出现过以国际条约作为引用法律依据的裁判文书。

没有法律效力的司法文件，如最高院研究室的《批复》，或者《座谈会纪要》之类，当然不能作为定案的法律依据。但是，这些文件与国际条约都可以在判决书的说理部分引用，以加强说理。

但是最重要的是，不要援引《宪法》

齐玉玲案_百度百科我就直接搬运百度百科的内容了

1990年，齐玉苓与陈晓琪都是山东省滕州市第八中学的初中学生，都参加了中等专科学校的预选考试。陈晓琪在预选考试中成绩不合格，失去继续参加统一招生考试的资格。而齐玉苓通过预选考试后，又在当年的统一招生考试中取得了超过委培生录取分数线的成绩。山东省济宁商业学校给齐玉苓发出录取通知书，由滕州八中转交。陈晓琪从滕州八中领取齐玉苓的录取通知书，并在其父亲陈克政的策划下，运用各种手段，以齐玉苓的名义到济宁商校就读直至毕业。毕业后，陈晓琪仍然使用齐玉苓的姓名，在中国银行滕州支行工作。

一审判决作出后，齐玉苓向山东省高级人民法院提起上诉，除了对精神损害赔偿的标准提出异议以外，主要是提出证据表明自己并未放弃受教育权，被上诉人确实共同侵犯了自己受教育的权利，使自己丧失了一系列相关利益。据此请求二审法院判决：（1）陈晓琪赔偿因侵犯姓名权而给其造成的精神损失5万元；（2）各被上诉人赔偿因共同侵犯受教育权而给造成的经济损失16万元和精神损失35万元。

山东省高级人民法院在审理中认为，这个案件存在适用法律方面的疑难问题，因此依照《中华人民共和国人民法院组织法》第32条[1] 的规定，报请最高人民法院进行解释。最高人民法院经过研究后，作出了《关于以侵犯姓名权的手段侵犯宪法保护的公民受教育的基本权利是否应承担民事责任的批复》（以下简称《批复》）。该决定全文如下：

山东省高级人民法院：

你院1999鲁民终字第258号《关于齐玉苓与陈晓琪、陈克政、山东省济宁市商业学校、山东省滕州市第八中学、山东省滕州市教育委员会姓名权纠纷一案的请示》收悉。经研究，我们认为，根据本案事实，陈晓琪等以侵犯姓名权的手段，侵犯了齐玉苓依据宪法规定所享有的受教育的基本权利，并造成了具体的损害后果，应承担相应的民事责任。

山东省高级人民法院在接到《批复》以后，继续审理此案并认为：

"……由于被上诉人滕州八中未将统考成绩及委培分数线通知到齐玉苓本人，且又将录取通知书交给前来冒领的被上诉人陈晓琪，才使得陈晓琪能够在陈克政的策划下有了冒名上学的条件。又由于济宁商校对报到新生审查不严，在既无准考证又无有效证明的情况下接收陈晓琪，才让陈晓琪冒名上学成为事实，从而使齐玉苓失去了接受委培教育的机会。陈晓琪冒名上学后，被上诉人滕州教委帮助陈克政伪造体格检查表；滕州八中帮助陈克政伪造学期评语表；济宁商校违反档案管理办法让陈晓琪自带档案，给陈克政提供了撤换档案材料的机会，致使陈晓琪不仅冒名上学，而且冒名参加工作，使侵权行为得到延续。该侵权是由陈晓琪、陈克政、滕州八中、滕州教委的故意和济宁商校的过失造成的。这种行为从形式上表现为侵犯齐玉苓的姓名权，其实质是侵犯齐玉苓依照宪法所享有的公民受教育的基本权利。各被上诉人对该侵权行为所造成的后果，应当承担民事责任。

由于各被上诉人侵犯了上诉人齐玉苓的姓名权和受教育的权利，才使得齐玉苓未接受高等教育另外再进行复读，为将农业户口转为非农业户口交纳城市增容费，为诉讼支出律师费。这些费用都是其受教育的权利被侵犯而遭受的直接经济损失，应由被上诉人陈晓琪、陈克政赔偿，其他各被上诉人承担连带赔偿责任。……

为了惩戒侵权违法行为，被上诉人陈晓琪在侵权期间的既得利益（即以上诉人齐玉苓的名义领取的工资，扣除陈晓琪的必要生活费）应判归齐玉苓所有，由陈晓琪、陈克政赔偿，其他被上诉人承担连带责任。……

综上，原审判决认定被上诉人陈晓琪等侵犯了上诉人齐玉苓的姓名权，判决其承担相应的民事责任，是正确的。但原审判决认定齐玉苓放弃接受委培教育，缺乏事实根据。齐玉苓要求各被上诉人承担侵犯其受教育权的责任，理由正当，应予支持。"

由此，山东省高级人民法院依照宪法第46条和最高人民法院的批复，对枣庄市中级人民法院的一审判决予以部分维持、部分撤销，并判决：（1）被上诉人陈晓琪、陈克政赔偿齐玉苓因受教育的权利被侵犯造成的直接经济损失7,000元，被上诉人济宁商校、滕州八中、滕州教委承担连带赔偿责任；（2）被上诉人陈晓琪、陈克政赔偿齐玉苓因受教育的权利被侵犯造成的间接经济损失（按陈晓琪以齐玉苓名义领取的工资扣除最低生活保障费后计算）41,045元，被上诉人济宁商校、滕州八中、滕州教委承担连带赔偿责任；（3）被上诉人陈晓琪、陈克政、济宁商校、滕州八中、滕州教委赔偿齐玉苓精神损害费50,000元。

这个案件被称为"宪法司法化第一案"而被法学人士津津乐道，它一审判决的法律依据是《民法通则》第120、134条，二审判决的法律依据是《宪法》第46条、《教育法》第9条、第81条，《民法通则》第120、134条，《民事诉讼法》第152、153条第1款第3项、第158条和《关于以侵犯姓名权的手段侵犯宪法保护的公民受教育的基本权利是否应承担民事责任的批复》。但是，这个《批复》在2008年12月18日被最高人民法院废止，理由是"已停止适用"。

再之后最高人民法院发文件通知各级法院不得再在裁判文书中援引宪法，只能从法律这一级别开始援引。

曾经有一个马伯里诉麦迪逊案的机会放在我们面前，但我们没有珍惜，直到失去才追悔莫及。。。。


4、不要作死之二：不要评价法律文件的效力

2003年5月27日，河南洛阳中级法院法官李慧娟在一个民事判决书里写

"《种子法》实施后，玉米种子的价格已由市场调节，《河南省农作物种子管理条例》作为法律阶位较低的地方性法规，其与《种子法》相冲突的条文自然无效"

河南省人大很生气，认为这个做法是侵犯了他们的立法权。
10月18日，河南省人大常委会办公厅下发了《关于洛阳市中级人民法院在民事审判中违法宣告省人大常委会通过的地方性法规有关内容无效问题的通报》，要求河南省法院"对洛阳市中级人民法院的严重违法行为作出认真、严肃的处理"。
随后，洛阳市中院作出决定，撤销判决书签发人民事庭副庭长赵广云、审判长李慧娟的职务。

该案二审中，河南省高院直接向最高院请示。最高院以【2004】民二他字第6号答复：

《中华人民共和国立法法》第79条规定：法律的效力高于行政法规、地方性法规、规章。行政法规的效力高于地方性法规、规章；最高人民法院《关于适用＜中华人民共和国合同法＞若干问题的解释（一）》第4条规定：合同法实施以后，人民法院确认合同无效，应当以全国人大及其常委会制定的法律和国务院制定的行政法规为依据，不得以地方性法规、行政规章为依据。


这个是绝大多数对法律有所了解的人都听说过的河南种子条例案，有兴趣的人可以继续去搜详细资料。这个李法官据说后来复职了，本案更多的是影响学术界对人民法院司法审查权的深入探讨。


但是，在实务界，最高人民法院在2009年10月26日发布的一个文件，很多人都没注意。
最高人民法院关于裁判文书引用法律、法规等规范性法律文件的规定

第七条　 人民法院制作裁判文书确需引用的规范性法律文件之间存在冲突，根据立法法等有关法律规定无法选择适用的，应当依法提请有决定权的机关做出裁决，不得自行在裁判文书中认定相关规范性法律文件的效力。


按《立法法》第99条的规定，想要确认一份地方性法规违宪或违法，只能向全国人大常委会书面提出审查申请。在裁判文书中，如果法官认为某一法律条文无效，只能说"我不用它"，不能说"它无效"。

第二个马伯里诉麦迪逊案的机会放在我们面前，但我们还是没有珍惜。。。。


二、不同法律的引用顺序

1、先引用法律，然后引用法律解释，然后引用司法解释。

如村干部犯的受贿罪，先引用《中华人民共和国刑法》，然后引用《全国人民代表大会常务委员会关于<中华人民共和国刑法>第九十三条第二款的解释》，最后才引用《最高人民法院、最高人民检察院关于办理贪污贿赂刑事案件适用法律若干问题的解释》。

2、法律与法律之间，先引用基本法，再引用其他法律；先引用刑事法律，再引用其他法律。

如刑附民判决书中可能会需要引用《民法通则》和《侵权责任法》。就要先引用《刑法》，然后是《民法通则》。这两个基本法引用完，再引用全国人大常委会发布的《侵权责任法》。

3、先引用《刑法》，再引用单行刑法《全国人大常委会关于惩治骗购外汇、逃汇和非法买卖外汇犯罪的决定》。

4、先引用实体法，再引用程序法.

常见的如二审改判的案件，应该是先引用《刑法》，再引用《刑事诉讼法》。



三、同一法律的条文引用顺序

1、如果是法律解释或司法解释，按条文的排列顺序引用。即从第1条到第100条的顺序引用。

2、如果是刑法的法条，按以下顺序引用：

  • 定罪——一般按条文排列顺序，但要先列援引法条，后列被援引法条。如转化型抢劫罪的条文顺序是"依照《刑法》第269条、第263条之规定"
  • 量刑幅度的单独条文。如果有多个罪名时，一般是按"A罪名+量刑幅度，B罪名+量刑幅度"的顺序
  • 具体刑罚——先主刑，后附加刑。然后才是刑罚的具体适用如限制减刑等。
  • 量刑情节——也是按条文排列顺序
  • 第64条——有的人认为第64条要放在最后引用，也有的人认为要放到具体刑罚的位置引用。

例：一个法院院长通过自己职务影响法官办案，并收受1亿元贿赂、使人民利益遭受重大损失的受贿罪，有自首情节，需要判死缓并限制终生监禁，没收其违法所得。适用的法条顺序为：

  • 第388条（以受贿论，援引法条）
  • 第385条第1款（被援引法条，受贿罪）
  • 第386条（援引量刑法条）
  • 第383条第1款第3项、第4款（被援引的量刑幅度与终身监禁）
  • 第48条（主刑：死刑）
  • 第57条（附加刑1：剥夺政治权利）
  • 第59条（附加刑2：没收财产）
  • 第67条第1款（量刑情节：自首）
  • 第64条（没收违法所得）


四、同一法律的表述

我国刑法发展到现在，在不同的时期可能条文的规定不同，如1996年用的是1979刑法，2010年的生产销售假药罪用的是被修订前的刑法。这些情况在引用时的表述也不同。

1、不同时期的刑法

  • 如果是79刑法，表述为"1979年《中华人民共和国刑法》"
  • 如果是现行刑法，表述为"《中华人民共和国刑法》"

排列顺序上，按时间顺序，先列79刑法，再列现行刑法

2、不同版本的刑法

  • 如果是没被修订过的法条，表述为"《中华人民共和国刑法》第X条"
  • 如果是被修订过的法条，要用现行有效的版本，表述为"《中华人民共和国刑法》第X条"
  • 如果是被修订过1次的法条，要用旧版本，表述为"1997年修订的《中华人民共和国刑法》第X条"
  • 如果是被修订过2次的法条，要用没被修订过的版本，表述为"1997年修订的《中华人民共和国刑法》第X条"
  • 如果是被修订过2次的法条，要用被第一次修订过的版本，如组织、领导、参加恐怖组织罪被刑法修正案3、刑法修正案9两次修订，要用修正案3之后、修正案9之前的版本，表述为"经2001年《中华人民共和国刑法修正案三》修正的《中华人民共和国刑法》第120条"

（网络不好，经常编辑后保存不了，如果有错误请提醒我）



来源：知乎 www.zhihu.com
作者：知乎用户（登录查看详情）

【知乎日报】千万用户的选择，做朋友圈里的新鲜事分享大牛。 点击下载
时间： 没有评论:

写给最开始的小白——水文地质到底是个什么玩意儿？

这篇文章讲了什么：

  • 专业研究的都是什么？
  • 为什么需要研究这些？
  • 我们需要掌握哪些技能才能学好这个专业？
  • Tips——大局观比细节更重要


Part1 我们在研究些什么？


自从笔者开始活跃在知乎上后，接到很多私信，最开始的问题总是始于"这个专业到底是干什么的啊？"——网上对于"水文地质"或者"地下水科学与工程"专业的介绍很多，但大多冗长且对于初学入门者来说太长又太晦涩。那么，笔者争取用最短的篇幅，把它讲的明白些，且对于有志留学的朋友，笔者加入了所有专业名词的英文，希望可以让你们对专业术语的英文能有些最开始的感性认知。

嗯，首先让我们来看一张图（怕是一张在之后的专业课每个老师都会给你们看的图）

水文循环（water cycle/ hydrological cycle/hydrologic cycle）


改进自：canada.ca/en/environmen


简单来说，这就是一滴水在地球上的命运，这个循环可以从任何一个环节开始然后周而复始。而对于水文地质学家（hydrogeologist），我们的主要关注的过程就是，雨水在落地后的入渗（percolation/infiltration）以及地下水（groundwater）在含水层（aquifer）里的形成、分布、运动和变化。然而水文循环的任意环节，都与地下水有着千丝万缕的紧密联系，尤其是与地表水之间的水量，水质的交换——是一定需要被统一起来的。在国内大部分情况下，地下水与地表水之间都是被分开研究，这实际上有点蠢哦。


那么，地下水究竟是什么？地下难道不是石头和土方吗？怎么会有水？


所以，下一个要科普的术语叫做 含水介质（aquifer media/medium）。

所谓含水介质，简单来说就是地下水在地下赋存的空间，水在岩土间的缝隙里绕着障碍物克服着艰险一直往前不停的流动，是不是感觉超牛X？ 下图是含水介质的一种——孔隙介质（porous media）示意图。


引自 frackoptima.com/usergui


那么，我们对地下水的研究，都包括什么呢？首先要明确的一点，研究一定为了应用。我们不妨打开地下水科学与工程的教学大纲看看——

总的来讲，本专业的应用包括但不限于地下水资源的勘查（prospecting）、评价 (assessment/evaluation)、开发 (exploitation)、管理(management)，地下水环境和地质环境的调查 (investigation)、监测 (monitoring)、评价和治理 (governance).

在此笔者引用了笔者本科母校中国地质大学（北京）的本科培养方案内容swre.cugb.edu.cn/jx/bks


Part 2 我们研究它干嘛？

Part 1其实已经承上启下的讲明，研究（research）必是为了应用（application），而应用必是因为有需求（demand）。这种需求，有不同的层面。

首先，从基本生存需求上来讲，水乃生命之源。地球有多么缺水，我们的国家有多么缺水不需再赘述。供水（water production）是一个区域，国家社会经济发展的基本。下图为北京市2017年的供水结构，地下水供水占到了总供水量的45%，而这一比例在历史上的干旱年所占的比例甚至高达65%。可见，地下水作为人类重要的水源，需要被得到重视，对其的研究十分必要。



引自：北京市2017年度水资源公报


其次，地下水资源作为一种战略资源，其合理的开采利用，是对一个地区甚至国家的发展起到决定作用的。目前地下水资源超采、污染，是在我国甚至世界范围亟需解决的问题。我国如今更是将生态文明建设作为国家发展的重中之重，祥参（paper.people.com.cn/rmr），那么，水文地质作为一个研究地下水为主体的学科，其研究的重要性与必要性，自然不必言说也显而易见。


再次之，对于地下水的研究，也是一些其他学科的辅助科学。如与地下水有密切联系的地质灾害、岩土工程等专业，在此先不一一赘述。但以此也可知，水文地质的触角不仅仅扎根于地质行业，更能触及到水利、城建、环保、交通等部门相关领域。


Part 3 我们需要有什么样的技能？

在这里，笔者想对技能（skill）先做一个简要的定义；在笔者看来，技能是承接"知识 （knowledge）"与"能力 （Capability）"的桥梁。纯熟的技能，可以将获取的知识转化为解决问题的能力。

知识可以通过教授或者自我学习在短时间内获得。而技能，确实需要在日久天长中慢慢培养与锻炼。而针对于初入水文地质行业的新人们，究竟有哪些技能需要被培养呢？ 笔者自知粗浅，一直对于知识与技能之间的差异感觉很难界定。在这一部分里，欢迎大家与我进行更多的探讨，以进行添加与删减：

  • 理科思维——对于基础的工程科学的悟性
  • 地质人思维——对于地质现象，以及抽象的水文地质概念的想象与理解
  • 计算机操作——对于专业学科软件的熟练使用
  • 野外能力——对于体能还有方向感这种天生无解的东西
  • 语言能力——至少，好好学学英语吧？
  • 质感——

这里相对质感这个概念，想要做出一个解释。笔者认为，对于任何事物的学习，都很考验个体对于研究对象的灵性。我一直不知道质感在英文里的准确翻译，我暂且将其定为"sensation"。水文地质的研究，多数时候是不可见（invisible）不可触（untouchable）的。因此，对于藏于层峦叠嶂中的这一汪水的研究，说白了，大部分时候靠猜想。但就像天生有人对数字敏感，而有人就是数学白痴一样。对于事物的领悟能力，是存在个体差异的。但我不将它定义为"天赋"是因为，我认为"质感"也是可以靠后天培养的。针对此，我会在之后开一篇专栏文章展开来讲。

暂且先这么多吧，因为实际上每个所罗列的技能里，都包含着很多东西，而作为开篇，这里先简明扼要的罗列一下就好啦。


Part 4 一个Tip

自认为一篇文章超过2K字就已经不会有人再读下去了，那么最后给一个tips作为我们的结语好了。

笔者认为，学习水文地质，是一个"一眼万年"的事情；我们如今所看到的河流山川，惊奇地貌，是远古至今大自然的鬼斧神工，我们的地球母亲用46亿年造就了这样的神迹，我们却需要用相对于46亿年的须臾——几十年的时间去认知她，何其之难却又何其美妙。

在我们的学习过程中，一叶障目时常发生；但朋友啊，请用更广阔的眼光，用宏观的思维来看待它。我们不需搞懂每一次考试里的每一个复杂的公式，但希望每学完一门课程。你闭上眼睛，所有的关键，所有的要点全部都在你的脑子里能织成一张壮阔的蓝图。知识总会被忘，但是只要蓝图在，你总能再找到他。

以上。



来源：知乎 www.zhihu.com
作者：刘大学 SidaLiu

【知乎日报】千万用户的选择，做朋友圈里的新鲜事分享大牛。 点击下载
时间： 没有评论:
订阅： 博文 (Atom)