文/应虹霞 视频/赵航
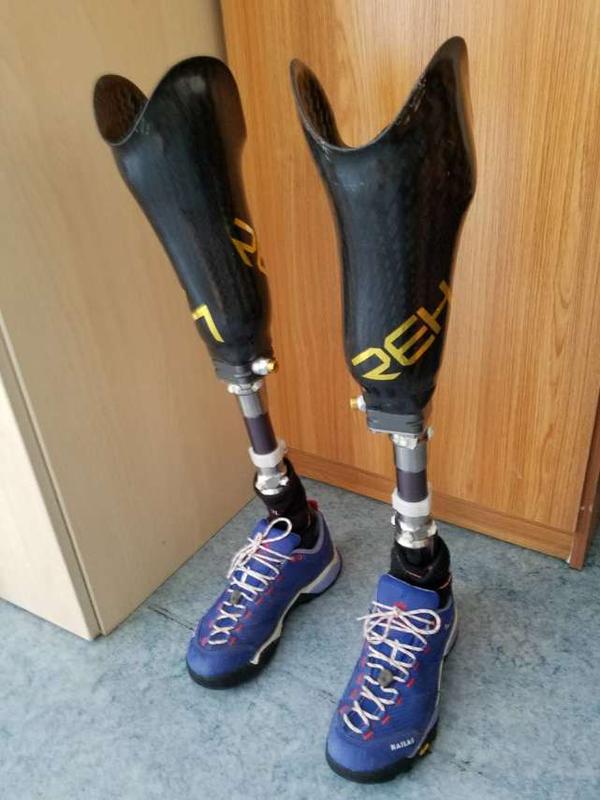
病床前数十公分,是一把轮椅;地面上,"站"着一副镫亮亮的假肢,足部"穿"着一双精神的运动鞋。雄赳赳的模样,一如其威武的主人。
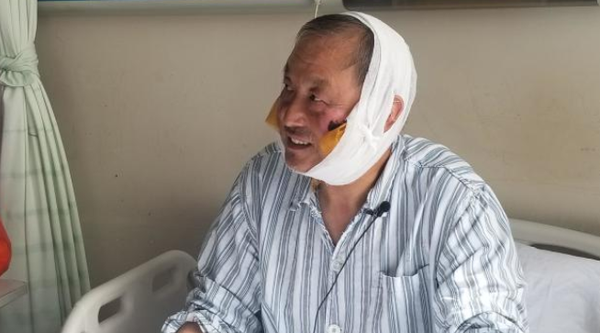
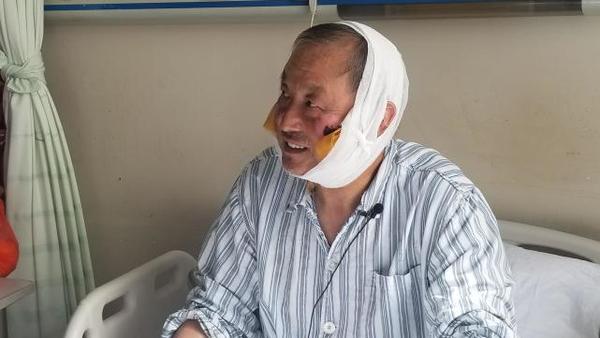
2018年5月22日,在北京某医院9楼93号病床见到了夏伯渝老人,四天前他刚刚从尼泊尔回到北京。北京时间2018年5月14日,69岁的无腿勇士夏伯渝人生第五次挑战珠峰,这次,他终于站上了43年来心心念念的地球之巅,一遂人生最大的梦想。(延伸阅读:69岁无腿老人登顶珠峰 曾身患癌症4次挑战失败)
接受采访的时候,因为冻伤,夏伯渝的脸上以及右手中指和无名指上还都缠着纱布。因为下肢肿胀厉害,他曾一度担心血栓复发,但入住医院的第一天便被医生排除,老人谈笑风声,心情相当愉悦。
划重点:
- 1 梦想43年终于达成:然而因为暴风雪突至,夏伯渝老人未能收获一张属于他的登顶纪念照。
- 2 攀登珠峰生死一线间:通往C5营地的20米小路成为最困难的一段路程。
- 3 冲击登顶代价大:此前四次尝试登顶珠峰,付出了失去双腿的代价,2016年离峰顶只差94米无奈放弃。
- 4 真的结束了:夏伯渝圆梦之后表示不再登山,不是他征服了珠峰,而是珠峰眷顾并接纳了自己。
"感谢珠峰眷顾了我,接纳了我"
"感谢珠峰眷顾了我,接纳了我。"69岁的时候,夏伯渝终于站上了43年来心心念念的地球之巅。
"一大片全是顶,其实我已经上(到珠峰)了,当时我还是往前走,能前进一步是一步。"走到顶部边缘,向导帮夏伯渝把安全带挂在一个安全锁上,让他坐下,因为太危险,不坐,就随时会摔下去。
夏伯渝往下俯瞰。眼前场景令他极度震撼——
那是一个悬崖峭壁。峭壁下,便是一片片乌云,很多小山头从云里冒出来,一个一个地,煞是壮观。8848米的地球之巅,真正的"会当凌绝顶,一览众山小"。
彼此彼刻,夏伯渝想与人分享这巨大的喜悦。第一个想到的,便是留守北京的爱人。
接过伙伴递上的对讲机,接通珠峰大本营,再转接北京。于是,便有了现在风靡网上的那段1分06秒的实时通话录音。
"你上去了吗,老夏?""我上来了,上来了。""一定要平安回来!"之后,夏伯渝的声音似乎消失在吱啦作响的无线噪音中。
那一刻,其实夏老已是泣不成声,泪流满面。"43年了,我完成了任务,但愧对家人。为了我的梦想我的理想,我很少顾家,也很少顾及他们的感受。所以当时觉得很激动,哭得挺厉害。"
再然后,同行的伙伴们一涌而上,围着他照相。

此时,暴风雪已经来了!一行人需要迅速下撤——一切发生在瞬息之间。
太过仓促。他来不及作出反应,甚至没有时间摆个POSE,来上一张属于他个人的登顶纪念照。43年了,他不止一次地遐想过,待到成功登上顶峰的那一天,自己要手指蓝天,拿着国旗挥舞。
这让他觉得美中不足,即便是此刻坐在北京的医院病床,回顾惊心动魄又激动不已的登顶一刻,夏伯渝仍在喃喃着,"很遗憾。"
两天后的5月16日,夏伯渝平安返抵大本营,惊喜地看到了儿子登登的身影。原来,这是团队的伙伴精心安排的,为的就是给夏老一个惊喜。看着儿子单薄的身体,听说他走了足有7、8天才到达珠峰大本营,夏老再次激动难抑。
20米小路生死一隙间 至今后怕"挂了"
69岁高龄,假肢——这种种意味着,夏伯渝第五次挑战珠峰之旅,一路困难重重,险象环生。
夏老承认,这是他最大的两个困难——而路途中最大的困难,是这次新增的一段不到20米的距离。其实在登峰之前,他原本已经把所有以往经历的路线都熟谙于心,但这次新增了一个C5营地。
这段让夏伯渝至今都后怕"挂了"的"未知的恐惧",坐落于主攀登路线到C5营地之间。这段不到20米的小路,又窄又斜,中间只拉着一根绳。关键是,它一会儿上,一会儿下,上下幅度很大,而夏老的假肢,弯曲幅度有限。

"像你们的腿一抬就可以抬到这儿,我只能顶多抬到这儿。它要是这么高的话,我够不着。因为我是下,所以得转过身,趴着,抓住绳,慢慢腿下去,够到那个地方,蹬实了,我才敢慢慢挪腿,太窄。上的时候也是,我也是腿抬不起来,只能爬....当时要知道这么费劲,这么危险,我就不会让设计C5,直接从C4就冲顶。"
小路的底下就是万丈深渊。夏伯渝说,当时自己根本没敢往下看。
危险还来自于天黑。从C5出发冲顶的时间,定在尼泊尔当地时间5月13日晚10点。
"上去(到C5)的时候还是白天,眼睛还看得见。上去登(顶)的时间是晚上10点,根本看不见。"出发冲顶前,伙伴们都抓紧时间躺下养心蓄锐,夏伯渝睡不着,一心想着这么黑的天,怎么才能第二次通过这段危险的小路。"即便是掉下去,也只有咬牙走。短短不到20米,我用了半个多小时。就跟打仗一样。"
再往上,困难依旧如影随形:狭窄的山脊,一面是万丈深渊,无数个冰裂缝;一面是大冰坡,一望无际的冰壁。没有健全的脚,夏伯渝必须调动两个登山杖,来感知雪的松紧程度,确认能不能挪动脚步。"我先用杖戮雪,看是不是实的,别往前一使劲就直接栽下去了,然后再迈步。健全人可以走直线,我不行,就跟爬差不多。"
最后的冲顶之路尽管困难,但夏伯渝心中有数,"心里有准备,就好说。"
腿部肿胀假肢"穿不上" 险些脱落在冰裂缝里
然而,攀登珠穆朗玛这样的世界第一高峰,意外随时随地就会来临。
第五次攀登珠峰的夏老,他的登山镜第一次出现了结冰。"以前都是雾。蹭一蹭就好,但这一次,必须摘掉手套,用手把冰一点点地抠掉。就几秒钟的功夫,手指就冻伤了。"
5月14日上午10时40分,夏伯渝成功登顶珠峰。随后,迅速下撤。此时,因为持续高强度的运动,他的腿部严重肿胀——假肢"穿不上了"
"本来假肢应该穿得很实,不会动,有螺丝卡着。但是穿不进去以后,它就悬着,跟活塞似地动。所以有两次,我的腿就踩到冰裂缝里,人掉了下去。"
让夏伯渝后怕的是,当时要是猛起脚的话——很有可能假肢就在冰裂缝里脱落,然后就"没了"。理智告诉他,没有假肢,在如此高的海拔,自己根本就下不来,也没有人能帮助自己下来。
他没敢动。怕腿在冰裂缝里,一动假肢就会脱落。他请向导过来,用工具设法把冰裂缝稍微扩大些,然后,再请向导抓住他的腿,小心翼翼地连腿带假肢拔出来——两次都是如此。
对于腿肿,夏老其实是有预案的。他携带了弹力绷带,肿的时候就把弹力绷带缠上,缩小肿胀程度。
但在下到7900米高度的时候,因为腿肿疼得无法忍受,夏老无奈只有松开弹力绷带,完全是靠着意志,一瘸一拐地往下走。踩着踩着,时间长了,残腿又进了假肢;进去后又胀疼,如此反复。
距离C2营地已然不远,看得到营地灯光在闪烁。但夏伯渝当时觉得,"自己真的是一步也走不动了。"
"向导说还有最后10分钟的路,实际我走了2到3小时。根本就走不动,一步一步往前挪。实在是走不到,把我走坏了......但还是坚持到了最后。"北京时间2018年5月15日晚11时,夏伯渝终于平安抵达C2营地。这,也意味着他真正意义上完成了成功攀登珠峰的壮举。
曾经,8848对他只是一串数字
"现在回想起来会觉得心疼,当时没有时间让你去想,我把睡袋给了别人我会冻死会怎么样。如果我有时间去想,可能我就会犹豫了。"
病床上的夏伯渝坚持不肯去坐轮椅,努力将身板挺得笔直。被截掉三分之一的双下肢看上去触目惊心,叫人心疼。
曾经,珠峰对夏伯渝而言,只是一个地理位置;8848对他只是一串数字,并无特殊的意义。
时钟拨回到1975年,国家登山队来到夏伯渝的运动队招聘队员。在那之前,夏伯渝是一名足球运动员。拿他的话来说,对登山,"没有一点概念"。
冲着能免费全面检查一次身体的朴素想法,夏伯渝报了名。因为过硬的身体素质,阴差阳错地,他成了百里挑一的幸运儿。"好像有一种虚荣心吧,到国家队,感觉比较光荣。所以就这样,我来到了登山队。"
1975年,夏伯渝所在的登山队领受了攀登珠峰的任务。"跟现在的商业登山不一样,那时确实是政治任务。原来要跟苏联联合登山,后来苏联撤了,总理亲自下令,就算是我们自己,也要登。"

1975年5月,登山队冲击珠峰,在距离峰顶200米下撤。途中,夏伯渝因为把睡袋让给了队友,冻伤了双脚,双下肢三分之一以下截肢。
"当时看见他的样子不太忍心,再想到我是(公认的)火神爷嘛,我不会冻伤,就把睡袋给了他。"那个晚上,因为连续多天的高强度攀登,没用睡袋的夏伯渝在疲倦中很快入睡,"没有感觉到冻伤的全过程,比如冻得疼,冻得发麻,直到失去知觉。"
夏伯渝至今清晰记得,直到第二天早晨,他还自己背着背包,从7600米高的营地走下了山,"没感觉到哪儿有不舒服的地方。"
那一年,他才26岁。
没有了脚,踢不了足球,人生梦想何在?一名外国假肢专家的一番话,让夏伯渝醍醐灌顶:安上假肢后,你不但可以像正常人一样的生活;你还可以再登山。既然可以再登山,那就再登珠峰吧!
何况,通过1975年这次登山,夏伯渝确认,自己的适应性和耐寒能力都很适应登山;登山过程的冒险和挑战也吻合自己年轻的心态,雪山上的美景,珠峰上飘着的旗云,也无不吸引着他——长达43年的珠峰情结,就此深埋心中。
人生中最艰难的决定——距离峰顶咫尺之遥放弃冲顶
"我穿假肢的过程,就是中国假肢发展的整个历程。"夏伯渝笑称。
在心中种下登珠峰的"草"后,夏伯渝的想法数十年来从未中断。并不成熟的假肢技术,成为横亘在现实与理想间的最大鸿沟。
直到2013年,中国的假肢技术达到了能够攀登珠峰的程度。同一年,夏伯渝跃跃一试去攀登珠峰,但因为摔伤,与第一次的机会擦肩而过。
事实上,在那之前的2008年4月,夏伯渝有过一次当奥运火炬手的经历。
"主要是两个目的。第一是体验穿假肢登山的感觉。其二是检测下我体能的适应性,因为毕竟几十年没有登过高山。"
循序渐进地,当年10月,夏伯渝第一次穿上假肢登雪山,攀登了海拔6178多米的青海玉珠峰。 2012年,又去攀登了海拔7546米的慕士塔格峰。这让他对自己的体能更加胸有成竹,而他也相应地改进了自己的假肢,以更适应登珠峰。
2014年,65岁的夏伯渝再次来到珠峰大本营,准备突击顶峰。不料,这一年尼泊尔遭遇珠峰登山史上最大的一次伤亡。因为雪崩,16名夏尔巴向导在珠峰遇难,尼泊尔政府取消了当年所有攀登珠峰的活动,没有人例外。
2015年,夏伯渝再次到达了珠峰大本营。没想到,这一次遭遇到了尼泊尔百年不遇的大地震。巨大的雪崩袭击了珠峰大本营,夏伯渝幸免于难。
"差一点就丧生在雪崩中。只要我活着,我就想,我一定要再登珠峰。"
2016年,再次来到珠峰的夏伯渝,经历了一次人生最难的决定——在上到海拔8750米,距离珠峰峰顶仅94米之际遭遇暴风雪,他决定下撤。
"就差94米。所有人到了这个高度,就会不顾一切地冲上顶峰。不管他能不能下得来。"事实上,当时夏伯渝也不是没有同样的想法:自己67岁了,又没有脚,且获悉尼泊尔政府出台了不准残疾人登珠峰的禁令。这,可能是自己最后一次冲击珠峰峰顶的机会了。
然而,当他回望到身后两名夏尔巴年轻向导求助的眼神时,他动摇了。
"他们都是以登山为职业的年轻人。我想,我不能为了自己的梦想而罔顾他人生命,那一瞬间,我做出了这一生最难作出的决定——下撤。"
此时,气温是零下20到30度。暴风雪一来,寒冷就会被成倍地放大。理智告诉他,不能有任何一丝的犹豫。"因为在那个高度,你要犹豫的时间太长,在不动的情况下很快就会冻伤。要么上,要么就下。"
走在回营地的路上,夏伯渝茫然若失,感觉怎么走也走不到。距离峰顶咫尺之遥放弃冲顶,"一直支撑自己的支柱没有了,就像大旗倒了一样。"
下撤回来后,夏伯渝才获悉,就他登顶的前后数天里,有6名登山者死于同一高度。
他庆幸自己作出下撤决定是正确的。"有点遗憾也不一定是坏事。如果没有当年的遗憾,我就没有今天。"
凌晨4点负重10公斤沙袋深蹲1500个
2018年,69岁的夏伯渝人生第五次站到了珠峰脚下。
之前四次与珠峰峰顶近在咫尺,虽然因种种遗憾无功而归,但夏伯渝从不认为自己是失败者。
在他看来,没登上去不在于自身,2016年的攀登经历反而检测了自己体能等各方面指标,也让他对之前的训练和努力有了自信。他坚信,只要天气良好,有朝一日一定可以登上珠峰。
关于禁止残障人士攀登珠峰的所谓禁令,也在悄然松动中——有人告诉夏伯渝,尽管尼泊尔出台了相关禁令,但是最终并未严格执行,而变成了"正在酝酿"。
这让夏伯渝的心又活泛起来。我,一定要赶上珠峰末班车!
不曾想,2017年,因为2016年从珠峰回来后得了血栓,医生严禁夏伯渝登山——登山运动量太大,如果再登山的话,血栓容易复发。尽管觉得医生的话不能全信但也不能不信,夏伯渝还是做好了准备再登珠峰的准备。
为了锻炼,不能登山,那就走戈壁,走沙漠,甚至去攀岩。一切都正常进行,不打无准备之仗。
不仅如此。

年龄,本来是夏老的一大短板。毋庸置疑,随着年纪一年年增长,人的体能和心肺功能都会下降。这是自然规律。
但夏老凭借顽强的毅力,愣是把劣势逆袭为自己的"优势"。"正因为我年纪每一年都在增大,所以我觉得我的体能训练,无论训练量和强度,比起年轻时候只能增,不能减。"
在准备第五次冲击珠峰的日子里,夏伯渝的每一天是这样渡过的。
每天早晨4点钟起床开始力量训练。内容是负重10公斤沙袋,练习深度下蹲,150个一组,练习10组;之后是仰卧起坐,30个一组,练习6组;再然后是俯卧撑,60个一组,练习6组。再配合背飞、练握力器等等力量的训练。
力量训练持续1个半到2个小时后,去登香山。夏伯渝的家距离香山20公里,他就选择骑自行车去。
"刚开始隔天登香山一次。后来,当我决定第五次攀登珠峰的时候,我就加大运动量,每天都练完体能后去登香山去。这样我才能够保持住体能,有足够的力量去登珠峰。"
自强者,天必助之。就在夏伯渝为再次攀登珠峰积蓄力量的同时,有国际人权组织帮助残障人士同尼泊尔政府对薄公堂,赢得了胜利。就这样,夏伯渝也得以有机会,在2018年之际返回心心念念的珠峰。
"生命是最重要的,不会盲目为理想去冒险"
"总算结束了!"
2018年5月16日,夏伯渝与迎接他的儿子一起,登上了飞往加德满都的直升机。回望皑皑白雪,挥别见证了自己生涯梦想的圣峰,老人百感交集。
他清楚,家人们知道他这一生受了很多苦,遭受了很多挫折打击,唯独就这一个心愿。他们不想让自己这一生留有遗憾,所以用种种方式支持自己。
他更深谙,家人们支持自己登山,并不是为了让他去登珠峰,而更看重的是他为了登珠峰努力锻炼的过程——登山的心愿,是他战胜病痛的精神支柱。
于是每一次登珠峰,家人们并不阻拦他,而他每一次也都说是最后一次。而因为大自然的捉弄,每一次又都不是最后一次。而在他的内心,他把每一次都当作最后一次,全力以赴,背水一战。这对自己也是一种激励和鞭策。

"不管怎么说,今年完成了梦想,家人也放心了。我也不会再去登山。真的结束了。"
回顾这次的成功登顶,他认为,这归功于梦想的力量和永不放弃的决心。
他从来没有遇到过什么人,笑话他的梦想。2016年,他在罗泊切山下碰见一名同样截去了小腿的美国大兵,一蹦一蹦地迎向他,鼓励他;2017年,他在前往珠峰大本营的路上遇上一个约旦朋友,后者同样戴着假肢,对他赞赏之余,笑称明年也要登珠峰。
他也从不考虑年龄。"我觉得年龄并不重要,重要的是心态。"他也觉得截肢,甚至因为血栓而得了淋巴癌都"没有什么","不管遇见挫折打击,我都要勇往直前在所不辞。"
即便自己成功登上了珠峰,他也不认为这是征服了珠峰——恰恰相反,是珠峰眷顾并接纳了自己。
"珠峰永远在那里,没人能征服它。一个人不管再强壮不可能征服大自然。在大自然面前,人太渺小。40多年了,珠峰终于对你敞开大门,说明珠峰对你的眷顾,对你勇敢的认可。这也是坚持的力量。"
对于理想与生命哪个更重要,夏老毫不含糊地选择了后者。
"当然生命是最重要的,我不会盲目地为理想而去冒险。我会在注意安全的前提下去实现我的理想。"
在成功登顶之后,夏伯渝也不止一次接到粉丝的电话,希望能跟他一起去登山,甚至登珠峰。
"能想到去登珠峰是有勇气的,是好事。但千万别盲目,一定要循序渐进。毕竟我以前是登山运动员,受过正规的训练,而且几十年来一直在努力锻炼,从没间断过。不然,你就是拿自己的生命开玩笑。"
凯旋回到北京的夏伯渝,还没有想好自己接下来做些什么。因为长年疲劳,他现在只想先静静地休整一段时间。在接受这次采访之前,除了家中至亲,夏老没有敢惊扰朋友们,但还是收到了众多的鲜花,还有朋友们的种种祝福,通过明信片、微信......
唯有一点是明确的。尽管这次完成了登山愿望,但夏老说,今后他还是会考虑从事一些有挑战性的运动项目——挑战,已然融入了他的生命。
来源:知乎 www.zhihu.com
作者:腾讯体育
【知乎日报】千万用户的选择,做朋友圈里的新鲜事分享大牛。 点击下载