经典网文分享

大家好！

这一节将会对基本群的定义，性质和应用做一个简单而全面的介绍。

提供之前的笔记：

我们开始本节的内容。本节内容对应原书内容为P109-

道路类

因为我们要讨论基本群，所以自然要涉及到代数中有关群的知识。因此也就需要它满足相关的群的性质。因此我们把基本群放在道路类意义下讨论。道路类的定义我们放在了上一节，为了强调，我们把它再次搬到这里。

Definition 1:
定义的所有道路在 $\simeq _.$ 下分成的等价类为的道路类，所有道路类的集合记为，一条道路所属的道路类记为，称的起终点为的起终点，如果起终点道路重合的道路类称为闭路类，并称其起终点为其基点。

这个意思是说，我们把所有的起点和终点相同的道路都划为一类。这样的话，就比较方便去建立基本群。

那么道路类有什么基本性质呢？

Proposition 1:
(1)若 $a \simeq_. b$ ，那么 $\bar a \simeq _ . \bar b$ 。
(2)若 $a \simeq_. b,c \simeq_. d$ ，并且有意义，那么 $ac \simeq_. bd$ 。

对于第一个，设 $H: a \simeq_. b$ ，那么只需要作 $H': I \times I \to X$ 为 H'(s,t) = H(1-s,t) （请注意两个单位闭区间不要弄混。同伦的定义中第一维是映射的原像变量，第二维是时间变量，而道路的原像变量的定义域正好是单位闭区间，所以这里的第一维变为 1-s ，相当于对道路取逆，而时间变量保持不变）。这样的话就可以得到 H'(s,t) 是一个 $\bar a$ 到 $\bar b$ 的定端同伦。

对于第二个，设 $H_1: a \simeq_. b,H_2: c \simeq_. d$ ，那么作 $H: I \times I \to X$ 为 $H(x,t) = \begin{cases}H_1(2s,t) & 0 \le s \le 1/2 \\ H_2 (2s-1,t) & 1/2 \le s \le 1\end{cases}$ ，那么容易验证满足条件。

其实这里的验证完全引用了之前介绍道路这个概念的时候的证明思路，只是多了一维时间变量作为摆设而已（当然，你需要说明这个同伦合理，也就是说 s=1/2 的时候不会出现什么问题）。

根据这两个性质，我们给出了道路类性质的新的定义。

Definition 2:
(1)规定道路类 $\alpha$ 的逆 $\alpha^{-1}=<\bar a>,a \in \alpha$ 。
(2)若道路类 $\alpha$ 的终点与 $\beta$ 的起点重合，规定 $\alpha,\beta$ 乘积为 $\alpha\beta=<ab>,a\in \alpha,b \in \beta$ 。

根据这些性质，马上就可以得到

Proposition 2:
$(\alpha^{-1})^{-1}=\alpha,(\alpha\beta)^{-1}=\beta^{-1}\alpha^{-1}$

是不是有点群的感觉了？

道路类运算如果仅仅是这样，还不足以吸引眼球，因为现在我们只能针对道路做操作。那么添加别的映射运算是不是就不行了呢？

Proposition 3:
设 $f: X \to Y$ 是连续映射，为上的两条道路，那么
(1)若 $a \simeq_. b$ ，那么 $f \circ a \simeq_. f \circ b$
(2)若可乘，那么 $f \circ a,f \circ b$ 可乘，且乘积为 $f \circ (ab)$
(3) $\overline{f \circ a}=f \circ \bar a$

对于第一个，我们 $H: a \simeq_. b$ ，那么 H(s,0)=a(s),H(s,1)=b(s) ，设 $H'=f \circ H$ ，那么这样的话依然是连续的，并且 $H'(s,0)=f(H(s,0))=f(a(s))=f\circ a(s)$ ，并且 $H'(s,1)=f(H(s,1))=f \circ b (s)$ ，这就构造出了满足条件的定端同伦。

对于第二个，一方面，可乘是容易验证的，另一方面，注意到乘积定义为 $ab(s)=\begin{cases}a(2s) & 0 \le s \le 1/2 \\ b(2s-1) & 1/2 \le s \le 1\end{cases}$ 。所以这样的话简单变量替换可得 $(f \circ a)(f \circ b)=\begin{cases}f \circ a(2s) & 0 \le s \le 1/2 \\ f \circ b(2s-1) & 1/2 \le s \le 1\end{cases}$ ，再对比一下 $f \circ ab$ ，是不是一样的？

对于第三个也是同理可得。

这个性质说明，道路类可以通过连续映射去映射到不同的拓扑空间。根据这个性质，我们构造一个新的对应 $f_\pi:[X] \to [Y]:f_\pi<a>=<f \circ a>$ 。这样的话，就有

Proposition 4:
$f_\pi(\alpha\beta)=f_\pi(\alpha)f_\pi(\beta),(f_\pi(\alpha))^{-1}=f_\pi(\alpha^{-1})$

这离引入代数结构又近了一步。

群还有一个关键的性质是结合律，那么如何体现在拓扑中呢？

Proposition 5:
道路类乘法有结合律。

我们只需要证明，对于 a(1)=b(0),b(1)=c(0) 的三条道路 a,b,c ，有 $(ab)c \simeq_. a(bc)$ 。那么规定 $f:[0,3] \to X$ 为 $f(t)=\begin{cases}a(t) & 0 \le t \le 1 \\ b(t-1) & 1 \le t \le 2 \\ c(t-2) & 2 \le t \le 3\end{cases}$ 。

之后怎么办呢？精彩的来了，设 $\tilde{a},\tilde{b},\tilde{c}$ 为 [0,3] 上的道路，并且满足 $\tilde{a}(t)=t,\tilde{b}(t)=t+1,\tilde{c}(t)=t+2$ 。那么就有 $f \circ \tilde{a}=a,f \circ \tilde{b}=b,f \circ \tilde{c}=c$ 。所以问题就转换到了 [0,3] 中的三条道路是否满足结合律。

要注意到的是，因为凸集中任意两条起终点相同的道路一定定端同伦，所以根据Proposition 3的第一个就可以得到 $(ab)c \simeq_. a(bc)$ ，这就证明了结论。

注意这里说的是道路类乘法有结合律。而不是道路本身有结合律，比方说 $(ab)c \ne a(bc)$ 就不成立（想想为什么）。通过这个性质就可以知道，我们建立基本群是一定要在道路类上去考虑的了。

下面是道路类中与群的单位元有关的性质。

Proposition 6:
设道路类 $\alpha$ 的起终点为，记 $e_{x_0},e_{x_1}$ 为处的点道路，那么
(1) $\alpha \alpha^{-1}=<e_{x_0}>,\alpha^{-1}\alpha=<e_{x_1}>$
(2) $<e_{x_0}>\alpha=\alpha=\alpha<e_{x_1}>$ 。

看上去挺显然的，但是怎么说明它呢？

设 e_0,e_1 分别为上在 0,1 处的点道路，取 $a \in \alpha$ ，就有 $e_{x_i}=a \circ e_i;i=0,1$ 。那么利用的凸性就有 $id_I\overline{id_I} \simeq_. e_0,\overline{id_I}id_I\simeq_. e_1,,e_0 id_I \simeq _.id_I \simeq_. id_Ie_1$ （因为它们都是一个凸集上的道路，并且起终点相同）。这样的话用复合可得结论。（比如说 $id_I \overline{id_I}(s)=\begin{cases}id_I(2s)& 0 \le s \le 1/2 \\ id_I(2s-1) & 1/2 \le s \le 1\end{cases}$ ，这样的话， $aid_I \overline{id_I}(s)=\begin{cases}aid_I(2s)& 0 \le s \le 1/2 \\ aid_I(2-2s) & 1/2 \le s \le 1\end{cases}=a \bar a$ ）

要注意的是，因为道路本身是一个映射，所以很多人容易把道路的乘积和映射的复合运算弄混。事实上判断一个凸集上的道路是否起终点相同，拿笔画一画就能看出来了。

这个命题说明点道路所在的道路类具有单位性。

铺垫好了，我们可以开始介绍基本群了。

Definition 3:
设为一个拓扑空间，取定 $x_0 \in X$ ，把的以为基点的所有闭路类的集合记为 $\pi_1(X,x_0)$ 。称这个集合在道路类乘法运算下构成的群为以为基点的基本群。

比如说设为 E^n 的凸集，那么注意到其中任意两条闭路定端同伦，这就意味着任意两条闭路在道路类意义下都是等价的。所以这个基本群只有一个元素，也称它为平凡群。

我们在上面介绍了，通过连续映射可以将定端同伦扩展到不同的拓扑空间内。这也就是 $f_\pi: [X] \to [Y]$ 。那么设 $x_0 \in X ,y_0 = f(x_0)$ ，则 $\alpha \in \pi_1(X,x_0)$ 时， $f_\pi(\alpha)\in \pi_1(Y,y_0)$ 。结合之前已经得到的道路类乘法的性质，可以得到以下的定义。

Definition 4:
若 $f: X \to Y$ 连续， $x_0 \in X,y_0 = f(x_0)$ ，那么 $f_\pi: \pi_1(X,x_0) \to \pi_1 (Y,y_0)$ 为诱导出的基本群同态。

注意到同态这里不唯一（因为 x_0 是任意取的），但都记作 $f_\pi$ 。

根据 $f_\pi$ 所定义的运算法则，容易得到

Proposition 7:
$(g \circ f)_\pi = g_\pi \circ f_\pi: \pi_1(X,x_0) \to \pi_1(Z,z_0)$

其中它们都是连续映射，且 y_0=f(x_0),z_0=g(y_0) 。

我们根据连续得到了同态，那么类比一下，根据同胚是不是可以得到同构呢？

Proposition 8:
若 $f: X \to Y$ 是同胚， $x_0 \in X,y_0=f(x_0)$ ，那么 $f_\pi: \pi_1(X,x_0) \to \pi_1(Y,y_0)$ 是同构。

事实上，证明 $f_\pi$ 是一个双射就可以了。

设 $g=f^{-1}$ ，并且设导出同态 $g_\pi: \pi_1(Y,y_0) \to \pi_1(X,x_0)$ ，那么 $g_\pi \circ f_\pi =(g \circ f)_\pi =id_\pi: \pi_1 (X,x_0) \to \pi_1(X,x_0)$ 是一个恒等同构。反过来也可以得到 $f_\pi \circ g_\pi$ 是一个恒等同构。

这能够说明什么呢？一方面根据 $g_\pi \circ f_\pi$ 是恒等映射可以得到 $f_\pi$ 是单射，反过来，根据 $f_\pi \circ g_\pi$ 是恒等映射，又可以得到 $f_\pi$ 是满射（想想为什么），这就证明了结论。

这个定理算是群在拓扑结构中的第一次比较好的应用。

基本群与基点的关系

我们之前讨论的都是在某一个空间下的某一个基点下生成的基本群。那么如果基点不同会出现什么呢？

Definition 5:
设 $\omega$ 为从到的一个道路类， $\alpha \in \pi_1(X,x_0)$ 。规定 $\omega_\#(\alpha)=\omega^{-1}\alpha\omega$ 为对应 $\omega_\#:\pi_1(X,x_0) \to \pi_1 (X ,x_1)$ 。

这是什么意思呢？相当于通过一个中介 $\omega$ ，构造一个基点为 x_1 的基本群。

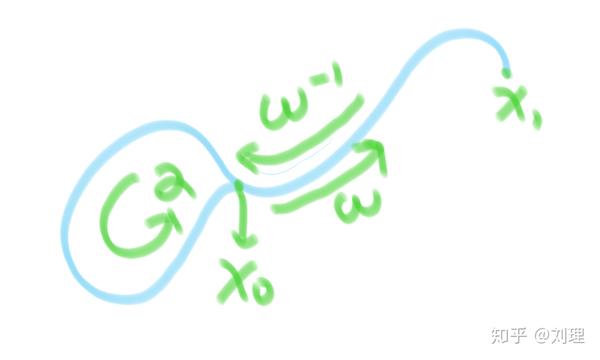
与之相关的一个性质如下

Proposition 9:
(1)若 $\omega'$ 为 $x_1 \to x_2$ 的道路类，那么 $(\omega\omega')_\#=\omega^{'}_\# \circ \omega_\#: \pi_1 (X,x_0) \to \pi_1(X,x_2)$ 。
(2) $\omega_\#:\pi_1(X,x_0) \to \pi_1(X,x_1)$ 是同构。

对于第一个，只需要设 $\alpha \in \pi_1(X,x_0)$ ，然后走定义即可。关键是第二个。

说明一个映射是同构，这里关键是要说明两点：同态，双射。说明同态就是要说明 $\omega_\#(\alpha)\omega_\#(\beta)=\omega_\#(\alpha\beta)$ ，这个地方走定义就好。而说明双射，注意到 $\omega_\#^{-1} \circ \omega_{\#} = (\omega \omega^{-1})_\#=<ex_0>_\#$ 为恒同映射（因为 $<ex_0>_\#(\alpha)=\alpha$ 可以由Proposition 6得到）。而 $\omega_\# \circ \omega_{\#}^{-1}$ 也一样。所以根据Proposition 8中相同的证明过程可得它是一个双射，也自然就得到了同构。

根据这个定义可以看出，如果 x_0,x_1 在的同一道路分支中，那么就会有结论 $\pi_1(X,x_0) \simeq \pi_1(X,x_1)$ 。而且每一个道路类（里面所有的道路的起终点相同）都可以决定一个同构。那么如果这个空间是道路连通的，那么这个时候，任何的两个基点之间的闭路类都是同构的。所以我们可以认为这个基本群与基点的选择无关。所以我们设它就为的基本群，记为 $\pi_1(x)$ 。

S^n的基本群

从这一节开始我们开始关注一些更加具体的有关基本群的计算。这个地方主要是说明 $S^1,S^n(n \ge 2)$ 的计算方法。

首先来看 S^1 （单位圆周）。首先把它放在复平面上考虑，也就是说设 $S^1=\{z \in \mathbb{C} \mid ||z||=1\}$ ，并且取 $z_0=1 \in S^1$ 为基点。所以你应该能想象出来，在 z_0 上的回路一定是在这个单位圆周上跑而得到的。

规定连续映射 $p: E^1 \to S^1;p(t)=e^{i2\pi t}$ 。下面说明它在局部上是同胚的。设 J_t=(t,t+1) ，那么有 $p|J_t:J_t \to S^1$ 是嵌入映射（这就相当于在模拟逆时针跑一圈的过程），并且如果设 $p_t=p|J_t:J_t \to S^1 \backslash \{e^{i2\pi t}\}$ ，就会有 p_t 是同胚映射，这个是不难验证的。

注意，上面所有的定义的映射，会贯穿这一部分的所有内容。

下面给出我们需要使用的相关定义。

Definition 6:
设是一个拓扑空间， $f: X \to S^1$ 连续，如果存在一个从到的连续映射 $\tilde f: X \to E^1$ 满足 $p \circ \tilde f =f$ ，那么称 $\tilde f$ 是的一个提升。

提升的定义事实上是提供了一个中介。因为我们要通过跑的圈数来判断同构，所以这个时候把所有的映射转化为上的映射自然是好的。

下面是几个与提升有关的引理。

Lemma 1:
若非满， $x_1 \in X ,t_1 \in E^1$ ，且有，那么存在的提升 $\tilde{f}$ ，使得 $\tilde{f}(x_1)=t_1$ 。

首先，因为不是满射，所以我们可以考虑取 $z=e^{i2\pi t} \not \in f(X)$ （这里我的考虑是因为 S^1 本身是具有对称性的，所以一定会有一个点不在值域内，那么挖掉哪一个都是一样的），这样就有 $f(X) \subset S^1 \backslash \{z\}$ 。这样的话，因为不在值域内，所以 $p(t_1)=f(x_1) \ne z$ ，那么根据我们之前对 p_t 的定义可知，一定存在一个整数使得 $t_1 \in J_{t+n}$ 。规定 $\tilde f=i_{t+n} \circ p_{t+n}^{-1} \circ f$ ，其中 $i_{t+n}:J_{t+n} \to E^1$ 为包含映射，容易验证这就是满足条件的提升（这是考虑到了 $p \circ i_{t+n}=p_{t+n}$ ）。那么自然也就容易看出来 $\tilde f(x_1) = t_1$ 。

Lemma 2:
设是上的道路， $t_0 \in E^1$ ，且。那么存在的唯一提升 $\tilde {a}$ 使得 $\tilde{a}(0)=t_0$ 。

先说明它的存在性。我们取 $m \in \mathbb{N}^+$ ，将等分为个小区间 $I_1,I_2,\cdots,I_n$ ，其中 $I_i=\left[\frac{i-1}{m},\frac i m\right]$ ，使得 $a|_{I_i}$ 均不满（直观上这是很好理解的）。那么根据Lemma 1，顺次规定 $a|_{I_i}$ 的提升 $\tilde{a_i}$ 使得 $\tilde{a}_1(0)=t_0,\tilde{a}_{i+1}(\frac i m)=\tilde{a}_i(\frac i m )$ 对于任意的 $i=1,2,\cdots$ 成立（这一块可能会很容易被迷惑，重新解释一下就是说，我们把一条道路拆成了块，那么这样的话， p(t_0)=a(0) 的意思是说，在 t_0 这个时刻，对应的这个映射的点是 a(0) ，这个映射的原像对应点为，所以规定的提升 $\tilde{a}_1$ 是把映射到 t_0 。当第一段道路走完后，对应的点为 a(1/m) ，对应的原像为 1/m ，这也是第二段道路 a_2 开始的点的原像。提升的意思就是把映射原像映射到时间变量上。所以此时的时刻变成了 $\tilde{a}_1(1/m)$ 。所以这个提升 $\tilde{a}_2$ 就是把映射原像 1/m 映射到时间 $\tilde{a}_1(1/m)$ 上，以此类推）。

根据粘接引理，把它们合起来的映射 $\tilde{a}:I \to E^1$ 连续，那么它还是的提升，并且有 $\tilde{a}(0)=\tilde{a}_1(0)=t_0$ ，就证明了结论。

接下来说明唯一性。如果 $\tilde{a},\tilde{a}'$ 都是的提升 z_0 ，那么设 $f=\tilde{a}'-\tilde{a}: I \to E^1$ 。那么对于任意的 $t \in I$ ，注意到 $p(f(t))=p(\tilde{a}'(t)-\tilde{a}(t))=p(\tilde{a}'(t))/p(\tilde{a}(t))=a(t)/a(t)=1$ （注意到的定义是 $p(t)=e^{2\pi i t}$ ）。所以这样的话，可以得到 f(t) 是整数。但是要注意到连续，且连通，所以只能得到它是常值函数。又因为 $\tilde{a}(0)=\tilde{a}'(0)$ ，所以 f(0)=0 ，这样的话，对于任意的 $t \in I$ 都有 f(t)=0 ，这就足够证明结论了。

事实上，在证明中我们得到了，同一个道路的两个提升在每一个固定的时间点上二者只会相差一个相同的常数。也就是说 $\tilde{a}'(1)-\tilde{a}(1)=\tilde{a}'(0)-\tilde{a}(0)$ 。移项可得 $\tilde{a}(1)-\tilde{a}(0)=\tilde{a}'(1)-\tilde{a}'(0)$ 。所以这个量它是与不同的提升无关的。所以回到闭路类，我们根据这个性质，提出一个新的概念。

Definition 7:
定义 $\tilde{a}(1)-\tilde{a}(0)$ 为以为基点的的闭路的圈数，记为。其中 $\tilde{a}$ 是的任一提升， $q(a) \in \mathbb{Z}$ 。

紧接着下面两个引理也就刻画了 S^1 的基本群的结构。

Lemma 3:
设是上基点为的两条闭路，并且 $a(t) \ne -b(t)$ 对于任意的 $t \in I$ 成立，那么。

取 a,b 的提升 $\tilde{a},\tilde{b}$ ，使得 $\tilde{a}(0)=\tilde{b}(0)=0$ 。设 $f=\tilde{a}-\tilde{b}$ ，那么 f(0)=0 。若 $q(a) \ne q(b)$ ，那么不妨设 q(a)>q(b) ，则 f(1) 是自然数，结合连续，可得 $\exists t \in I,f(t)=1/2$ ，也就是 $\tilde{a}(t)=\tilde{b}(t)+1/2$ 。这样的话 $a(t)=e^{i2 \pi \tilde{a}(t)}=-b(t)$ ，就矛盾了。

Lemma 4:
设是上基点为的闭路，那么 $q(a)=q(b) \Leftrightarrow a \underset{.}{\simeq}b$ 。

一方面，设 $H: a \underset{.}{\simeq}b$ ，那么记 h_t 为的t-切片，则注意到一致连续，可得存在 $\delta>0$ ，使得 $|(t_1,s_1)-(t_2,s_2)|<\delta$ 时，有 |H(t_1,s_1)-H(t_2,s_2)|<2 。这样的话，如果 $|t_1-t_2|<\delta$ ，那么对于任意的 $s \in I$ 有 $|(t_1,s)-(t_2,s)|=|t_1-t_2|<\delta$ 。这说明什么？说明 |H(t_1,s)-H(t_2,s)|<2 ，别忘了我们的这两个点都在 S^1 上，也就是说，这两个点不可能是对径点，所以也就是说，存在 $\delta>0$ ，使得 $|t_1 -t_2|<\delta$ 时，对于任意的 $s \in I$ ，有 $h_{t_1}(s) \ne -h_{t_2}(s)$ 。那么根据Lemma 3就可以得到 $q(h_{t_1})=q(h_{t_2})$ 。那么就可以说明 q(h_t) 的值并不依赖于。所以自然就可以得到 q(a)=q(h_0)=q(h_1)=q(b) 。

另一方面，作相同的提升，那么 $\tilde{a}(1)=q(a)=q(b)=\tilde{b}(1)$ 。所以 $\tilde{a},\tilde{b}$ 就是 E^1 上有相同起终点的道路，自然可以得到 $\tilde{a} \underset{.}{\simeq}\tilde{b}$ ，所以根据Proposition 3自然可以得到结论.

最后，就是我们这个精彩的大定理了。

Theorem 1:
$\pi_1(S^1,z_0)$ 是自由循环群。

不妨设 $\alpha \in \pi_1(S^1,z_0)$ ，规定 $q(\alpha) = q(a), a \in \alpha$ ，那么就有一个映射 $q: \pi_1(S^1,z_0) \to \mathbb{Z}$ 。

设 $\alpha = <a>,\beta = <b>$ ，那么作 a,b 的提升 $\tilde a, \tilde b$ ，使得 $\tilde a(1)= \tilde b(0)$ ，那么这样的话 $\tilde a \tilde b$ 为的提升，起终点为 $\tilde a(0),\tilde b(1)$ ，于是有 $q(\alpha\beta)=\tilde b(1)-\tilde a(0)=q(a)+q(b)=q(\alpha)+q(\beta)$ ，这就说明了保持了同态运算。之后，根据Lemma 4，又可以得到是单同态。

设 $a_0: I \to S^1$ 为 $a_0(t)=e^{i 2 \pi t}$ ，那么 q(a_0)=1,q(<a_0>)=1 ，且对于任意的正整数有 $q(<a_0)>^n)=n,q(<\bar a_0>^n)=-n$ ，这就证明了满同态，自然是同构。所以我们就证明了， $\pi_1(S^1,z_0)$ 是由 <a_0> 生成的自由循环群。