经典网文分享: 积和式, 玻色采样和计数复杂性

这篇会讲一讲积和式 (Permanent) 和 $\mathsf{\#P}$ -completeness, 以及玻色采样 (Boson Sampling) 之间的联系.

用以展示量子计算优越性 (quantum conputational supremacy)[6] 的候选问题有很多, 不过玻色采样 (Boson sampling) 很可能是知名度最高的问题之一. 这一问题的美妙之处在于, 它联系了线性光学和积和式 (permanent), 因为光子 (photon) 在不同的模数 (mode) 上的概率分布, 可以对应到某个积和式上; 而积和式在计算复杂性理论中具有独特的地位, 原因之一是它提供了第一个非平凡的 $\mathsf{\#P}$ -complete 问题. 有趣的是, 基于线性光学的技术给出了新的规约手段, 因而一并导出了一些特定类型的矩阵, 即 GL(n) , O(n) , U(n) , Sp(2n) 对应的积和式求值也是 $\mathsf{\#P}$ -complete 的[1].

本文的部分细节来自 Daniel Grier 上周的 seminar[1], 以及 2016 年 Scott Aaronson 在 Avi60 上的 talk[2]. 本文亦发表于我的博客, 见积和式, 玻色采样和计数复杂性 - Complexity Meets Quantum.

积和式与全同粒子

与行列式相比, 积和式相对要少见得多. 部分原因可能是行列式的性质相比之下要好得多, 比如说同态性质使得行列式能够被有效地计算; 而积和式在计算上的困难有些出人意料, 这一问题甚至是 $\mathsf{\#P}$ -complete 的 (至少和 $\mathsf{NP}$ -complete 一样困难), 于是对积和式的刻画也使得我们能够对计数复杂性类 $\mathsf{\#P}$ 有更多地了解. 除此之外, 行列式和积和式也被用于描述量子力学中的全同粒子 (idential particles), 下面会从不同方面简单的介绍积和式及其联系.

计数复杂性类: 计算积和式有多难

通常在第一学期的线性代数课程中会介绍行列式 (determinant), 我们可以用 Laplace expansion 导出其定义: 给定一个 $n \times n$ 矩阵 $A\in \mathbb{R}^{n \times n}$ , 那么行列式为 $Det(A) = \sum_{\sigma\in S_n} (-1)^{sgn(\sigma)} \prod_{i=1}^n a_{i,\sigma(i)},$ 这里的 S_n 是置换群, 里面的每个置换 (permutation) 都是其中的元素. 长的置换可以由短的置换合成, 显然最短的置换长度为, 那么 $sgn(\sigma)$ 表示的是置换 $\sigma$ 需要奇数 (或偶数) 个-置换合成. 类似地, 我们也可以定义积和式

$Per(A)=\sum_{\sigma\in S_n} \prod_{i=1}^n a_{i,\sigma(i)}.$

尽管它们都是对置换群中的所有置换求和, 但是使用了置换奇偶性的行列式的性质要好得多: 行列式有同态 (homomorphism) 性质 Det(AB)=Det(A)Det(B) , 那么一次 LU 分解足以完成行列式求值. 这意味着一个令人惊讶的事实: 尽管看起来我们需要对指数多项求值, 但是行列式求值有多项式时间算法!

事实上我们知道 $\mathsf{Determinant} \in \mathsf{NC}^2\subseteq \mathsf{P}$ , 即行列式求值可以由深度为 $O(\log^2 n)$ 的布尔线路 (Boolean circuit) 在时间 $O(\log^2 n)$ 内完成. 但是对于积和式, 由于没有同构性质, 我们必须对指数多项求和 -- 即使是已知的最好的经典算法, 积和式的精确计算的时间复杂度仍然需要 O(n2^n) . 不过这事也不绝对, 如果把积和式求值限制在有限域 $\mathbb{F}_2$ 上, 多项式时间算法显然是存在的 -- 因为这时候积和式和行列式等价. 事实上实数域上的-积和式求值, 在 1979 年被 Leslie Valiant 证明是 $\mathsf{\#P}$ -complete 的; 而 1991 年的 Toda 定理 $\mathsf{PH} \subseteq \mathsf{P}^{\mathsf{\#P}}$ , 则告诉我们计数复杂性类 $\mathsf{\#P}$ 比我们想象中大得多, 因而积和式求值也是一个比看起来困难的多的问题.

计数复杂性类 $\mathsf{\#P}$ 说的是这么一件事: 我们知道 $\mathsf{NP}$ 说的是至少存在问题的"一个解" (witness), 能够在多项式时间内被 (确定性 Turing 机) 验证; 而 # 即数数 (number), 所以 $\mathsf{\#P}$ 说的则是这样的"解"到底有多少个? 自然地, 我们从定义中知道 $\mathsf{\#SAT}$ 是 $\mathsf{\#P}$ 天然的完全 ( $\mathsf{\#P}$ -complete) 问题. 那么如何证明这一结果呢? Valiant 从给定的 $\mathsf{SAT}$ 实例 (instance) 出发, 利用变量 (variable) 和子句 (clause) 的关系构造了一个图, 然后考虑这个图的不相交圈覆盖 (cycle cover) 的个数 -- 可以证明它正比于这个图的邻接矩阵的行列式, 从而得到-积和式求值是 $\mathsf{\#P}$ -complete 的. 需要说明的是, 这一工作是 Leslie Valiant 在 2010 年荣膺 Turing Award 的三篇文献之一.

用积和式描述全同粒子

积和式并不是一个凭空出现的东西, 至少在量子力学里不是. 直觉上来说, 玻色子和费米子最大的不同之处在于, 玻色子会"扎堆", 而费米子会遵从 Pauli 不相容原理. 回到量子力学中的全同粒子 (identical particle) 公设, 用于交换序号的算符 $\hat{P}$ 的本征态对于对称态和非对称态来说是不一样的 (不考虑它们之间的相互作用), 这样的做法被称为一次量子化 (之所以这么叫是因为二次量子化, 不过这里有那么点历史包袱的意味). 具体来说, 非对称态加了个因子来表示置换的奇偶性 (想想上一节的置换群 S_n ). 这里的对称态对应的玻色子, 非对称态对应的是费米子, 两者的统计性质不同.

那么我们可以从单粒子波函数来构造全同粒子波函数, 遍历所有意味着遍历所有排列.

对于玻色子, 我们有 $\tilde{\psi_S} = \sum_{P} \hat{P} \psi_{k_1} (g_1) \psi_{k_2} (g_2) \cdots \psi_{k_N} (g_N);$
而对于费米子, 则是 $\tilde{\psi_A} = \sum_{P} (-1)^{sgn(P)} \hat{P} \psi_{k_1} (g_1) \psi_{k_2} (g_2) \cdots \psi_{k_N} (g_N).$

回忆一下上一节的积和式和行列式定义, 不难发现玻色子情形对应积和式, 而费米子情形对应行列式 (称为 Slater determinant). 注意到行列式有个性质, 如果两行(或列)一样的话, 那么行列式值为零 -- 这意味着 Pauli 不相容原理.

关于积和式和行列式还有个段子, 来自 Scott Aaronson[2]:

搬到 Austin 的 Aaronson 发现在 Steven Weinberg 的量子力学教材上, 上面俩式子都叫 Determinant. 于是他就问 Weinberg, 你是不是不知道这东西叫 Permanent, Weinberg 表示我当然知道, 但是我得假设别人不知道, 毕竟对物理学家来说这就是个式子.

众所周知, 玻色子的典型例子是光子, 而费米子的典型例子是电子. 既然光子如此司空见惯 (虽然积和式求值难如 $\mathsf{\#P}$ -complete), 这里会不会有什么新的想法来帮助我们计算积和式, 或者理解计数复杂性类 $\mathsf{\#P}$ 呢?

计算优越性: 玻色采样与积和式求值

到此为止, 我们知道作为全同粒子的光子, 实际上可以看成不可区分的球, 那么我们就回到了组合中常见的球和桶的模型. 于是 Scott Aaronson 师徒提出的玻色采样 (Boson Sampling)[3] 说的是这么件事, 假设你手上有个不可区分的球, 你需要把它们扔进个不同的桶里 (你技术很好不会扔到桶外面), 那么球最终在桶里的排布会是什么样的?

这里的个球就是光子,个桶则是模 (mode); 并且球是不可区分的, 而桶是可区分的. 当然扔球的过程和线性光学的实验设备有关, 具体什么样嘛可以看看这个网页游戏. 我们可以把这个问题数学化如下, 这里的实验设备由扔球矩阵刻画.

什么是玻色采样

问题的输入是不可区分球个数, 和可区分桶个数; 以及扔球矩阵 $A_{mn}$ 和想要的球排布 $S = (s_1,\cdots,s_m) \in \Phi_{m,n}$ , 其中 $\sum_{i=1}^m s_i = n$ . 扔球矩阵形式如下, $A=\begin{pmatrix} U_{11} & \cdots & U_{1n}\\ \vdots & \ddots & \vdots\\ U_{m1} & \cdots & U_{mn}\\ \end{pmatrix}.$

如果我们把扔球矩阵的第行重复 s_i 次, 那么我们可以得到一个综合了球排布和扔球矩阵的新扔球矩阵 A_S , 形式如下 ( $n \times n$ 矩阵): $A_S=\begin{pmatrix} U_{11} & \cdots & U_{1n} & \cdots & U_{1m}\\ \vdots & \ddots & \vdots & \ddots & \vdots\\ U_{m1} & \cdots & U_{mn} & \cdots & U_{mm}\\ \end{pmatrix}$

问题的输出是球排布出现的概率, 即占据数表象 (occupation-number representation) 下的波函数 $\mathrm{Pr}[S]=\frac{1}{s_1!\cdots s_m!} \langle s_1,\cdots,s_m|A_S|0,\cdots,0\rangle = \frac{|Per(A_S)|^2}{s_1!\cdots s_m!}.$ 为什么上面会涉及积和式呢? 分母很好理解, 因为我们的球是不可区分的. 对于分子, 积和式中的每一项都对应着某种球置换 (ball permutation), 符合给定的球分布意味着所有"桶"里都必须有球 (因为允许空桶, 所以这里又加了个球), 于是球排布出现的概率正比于新扔球矩阵 A_S 的积和式的值.

线性光学: KLM 定理

Aaronson-Arkhipov[3] 说的是, 如果存在求解上述玻色采样问题的有效经典(近似)算法, 那么会导致意想不到的计算复杂性后果 -- 我们相信这样的后果不可能出现, 就跟我们相信 $\mathsf{P} \neq \mathsf{NP}$ 一样.

展开说的话, 我们知道线性光学中量子计算并不是通用 (universal) 的, 因为某些量子门无法实现. 而在 2000 年, Knill, Laflamme 和 Milburn 指出[5], 如果允许延迟选择 (post-selection) 操作的话, 那么线性光学量子计算是 universal 的, 这一结果称为 KLM 定理. 即给定量子线路, 其中 CSIGN 门 (控制相位门) 个数为 $\Gamma$ , 并且 $|I\rangle = |0,1,\cdots,0,1\rangle$ , 有下述结果 $\langle I|\phi(L)|I\rangle =\frac{1}{4^{\Gamma}} \langle 0\cdots0 | Q | 0\cdots 0\rangle,$ 其中 $\phi(L)$ 是线性光学中对应的量子门, 具体做法如下:

用线性光学态表示量子态, 即用一个光子和两个模来 (一个球和两个桶) 表示一个量子比特 (称为 Dual-rail encoding),比如 $|0\rangle \rightarrow |1,0\rangle, |1\rangle \rightarrow |0,1\rangle.$
单量子比特门可以直接实现.
CSIGN 门实现如下, 进行对-模延迟选择, 使得下述约束 (共有 $4\times 4=16$ 个) 成立: $\langle 0,1|\phi(L)|0,1\rangle = 1 \Leftrightarrow \langle 1,0,0,1 |\phi(L)| 1,0,0,1\rangle = \frac{1}{4}.$

我们知道单量子比特门加上一个两量子比特门可以实现通用 (universal) 量子计算. 需要说明的是, 实际中的延迟选择和 $\mathsf{PostBQP}$ 中的延迟选择并不相同, 因为我们假设后者的延迟选择发生概率大于 1/2 (远远大于实验中的 1/2^n ), 所以后者的计算能力要强于通用量子计算机 (即 $\mathsf{BQP} \subseteq \mathsf{PostBQP} = \mathsf{PP}$ ).

玻色采样的计算优越性

玻色采样所讨论的采样问题, 准确地说是用非通用量子计算机 (线性光学量子计算) 来进行采样, 对上述 KLM 定理稍加改进, 那么对应的计算复杂性类是 $\mathsf{PosBQP}$ . 类似地, 如果我们对经典计算机 (这里讨论的是随机算法) 也允许延迟选择操作的话, 对应的计算复杂性类是 $\mathsf{PostBPP}$ . 这里的计算优越性是因为, 如果允许延迟选择操作后, 量子情形相对经典情形没有优势 (即 $\mathsf{PostBPP} = \mathsf{PostBQP}$ ) 的话, 那么 $\mathsf{PH}$ 塌缩到第三层: $\mathsf{PH} \subseteq \mathsf{P}^{\mathsf{\#P}} = \mathsf{P}^{\mathsf{PostBQP}} =\mathsf{P}^{\mathsf{PostBPP}}\subseteq \Delta_3$ 第一个包含关系是著名的 Toda 定理, 第二个则是 Aaronson 的工作, 第三个这里关于计算优越性的假设, 最后一个则是 Sipser-Gacs 定理. 关于 $\mathsf{PH}$ 的介绍和上述关系的更多介绍参见 Adam Bouland 在 It from Qubit Summer School 上的 talk[4].

关于量子计算优越性 (quantum computational supremacy) 的更多介绍, 参见 Aram Harrow 和 Ashley Montanaro 的科普[6]. 多上几句, 上述计算复杂性理论中的假设 (比如 $\mathsf{PH}$ 不会塌缩, 即 $\mathsf{P} \neq \mathsf{NP}$ 的一般化版本) 只是可能的假设 (assumptions) 之一, 除此之外还有

Fine-grained complexity (细粒化复杂性?): 即把 $\mathsf{SAT}$ 规约到某个问题上, 那么如果这个问题存在足够快 (比如说好于平方时间) 的多项式时间(经典)算法, 则会违背 exponential time hypothesis (ETH); 如果我们找到了好于上述 bound 的量子算法, 那么这里同样有计算优越性.
Average-case assumptions (平均情形): 这里关注平均情形下的 hardness. 比如说一个函数在某个分布上难以计算, 这意味着如果这里没有有效地经典算法, 能够对于从中采样得到的大部分输出. 最出名的例子应该是random circuit sampling.

需要说明的是, 体现计算优越性也可以不需要任何假设: 对于常数深度量子线路, Bravyi, Gosset 和 Koenig 给出了一个非常美妙的结果[7] (QIP 2018 plenary talk): 存在某个问题可以用常数深度 (constant-depth) 量子线路求解, 但是在经典情形下的则需要对数深度 (logarithmic depth) 概率线路 (probabilistic circuit), 这里不再展开.

经典定理的量子证明: 线性光学与新的规约技术

其实积和式和玻色采样还有一些时间上的巧合: 在关于玻色采样的工作被 STOC 2011 接收的两个月后, Leslie Valiant 就被宣布获得 2010 年的 Turing Award -- 而 Aaronson 的积和式计算是 $\mathsf{\#P}$ -complete 的证明一文更是简单直白, 为纪念 Valiant 的 Turing Award 而作.

Aaronson 的证明[8]给出了完全不同于 Valiant 的 $\mathsf{\#P}$ -completness 规约方式, 那么这样的借助线性光学量子计算的新技术. 能否告诉我们关于积和式和计数复杂性的更多结果呢? Grier 和 Schaeffer 给出了肯定答案[1], 他们证明了 GL(n) , O(n) , U(n) , Sp(2n) 上的矩阵对应的积和式计算仍然是 $\mathsf{\#P}$ -complete 的:

对于特征为的有限域 $\mathbb{F}_p$ ( $p \neq 2, 3$ ), 其上的矩阵的积和式的计算是 $\mathsf{Mod_pP}$ -hard 的.

需要说明的是, 这里的 $\mathsf{Mod_pP}$ 也是计数复杂性类, 不过需要模. 除此之外, 上述结果实际上是"二分 (dichotomy) 定理". 因为 p=2 是行列式和积和式等价, p=3 时有非平凡的经典算法 (Kogan 1996)[8]. 下面简单介绍如何用基于线性光学量子计算的规约技术, 证明酉矩阵的积和式计算是 $\mathsf{\#P}$ -complete 的.

证明路线和预处理

Aaronson 的证明[8]中讨论的问题如下:

输入: 给定的布尔函数 (Boolean function) $C:\{0,1\}^n \rightarrow \{0,1\}$ .
输出: $\Delta C := \sum_{x\in\{0,1\}^n (-1)^{C(x)}}$ , 可以验证 $\Delta C/2^n=\langle 0\cdots 0|Q|0\cdots 0\rangle$ .

为了证明积和式的计算是 $\mathsf{\#P}$ 的, 我们需要把输入实例 (instance)设法规约到积和式上, 即导出 $\Delta C \propto Per(L_{I,I})$ . 中间过程需要借助线性光学量子计算, 证明的大致路线如下:

把 $\Delta C$ 编码到量子线路上, 得到 $\langle 0\cdots 0|Q|0\cdots 0\rangle$ .
把量子线路对应到光学网络 (optic network)上.
最终得到积和式和线性光学量子计算的对应关系, 即

$\Delta C \propto \langle 0\cdots 0|Q|0\cdots 0\rangle \propto \langle 1,0,\cdots 1,0| \phi(L)|1,0, \cdots 1,0\rangle \propto Per(L_{I,I}).$

首先需要做的是把 $\Delta C$ 用量子线路和量子比特编码, 使用的量子线路如下:

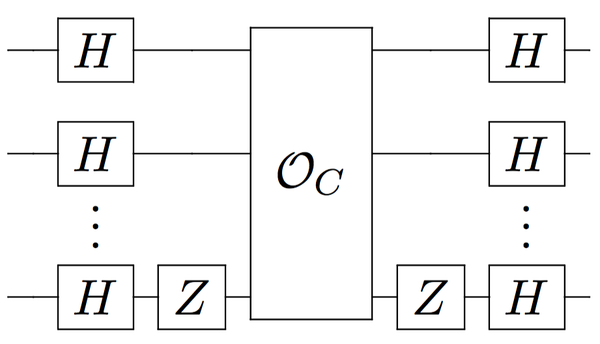
上述过程实际上就是量子 Fourier 变换, 展开来说的话: 我们知道 $H^{\otimes n}$ 可以把真空态 $|0\rangle^{\otimes n}$ 变成 computational basis 的均匀叠加 $\frac{1}{2^{n/2}}\sum_{x \in\{0,1\}^n} |x\rangle$ . 而门的作用则是提取出 $\{|+\rangle,|-\rangle\}$ 中的符号, 即对于 $|-\rangle = \frac{1}{\sqrt{2}}(|0\rangle+|1\rangle)$ , 我们有 $Z |-\rangle = -|-\rangle = (-1)^1 |-\rangle$ . 于是不难得到

$\begin{aligned} \langle 0\cdots 0|Q|0\cdots 0\rangle &= \frac{1}{2^n} \left( \sum_{x\in \{0,1\}^n} \langle x|\langle -|\right) C \left( \sum_{x\in \{0,1\}^n} |x\rangle |-\rangle\right)\\ &= \frac{1}{2^n} \sum_{x\in\{0,1\}^n} (-1)^{C(x)} = \frac{\Delta C}{2^n}, \end{aligned}$

即我们成功地把布尔线路编码到几率幅 $\langle 0\cdots 0|Q|0\cdots 0\rangle$ 上.

从线性光学到量子线路

首先回顾一下线性光学中量子态如何表示:个光子和个模, 可以看成个不可区分的球和个可区分的桶, 在占据数表象下我们有 $|s_1,\cdots,s_m\rangle$ , 即有 s_k 个光子在第个模上. 不难验证 Hilbert 空间的维度 $|\mathcal{H}| = \binom{n+m-1}{m-1} = \binom{n+m-1}{n}$ , 因为球在桶中 (允许空桶) 的不同排布有 $|\mathcal{H}|$ 中.

那么线性光学中的量子门是什么样的呢? 比如 Hadamard 门可以看成两个发射器一上一下自左向右平行发射了两个小球, 然后中间某一装置会把小球扔向右侧上方或下方的接收器, 往哪扔球的概率取决于(所以前文称作"扔球矩阵"). 令 $\phi(L)=H$ 的话, 不难得到 $\begin{aligned} \phi(L)|1,0\rangle &= \frac{1}{\sqrt{2}}(|1,0\rangle+|0,1\rangle)\\ \phi(L)|1,1\rangle &= \frac{1}{\sqrt{2}}(|2,0\rangle-|0,2\rangle)\\ \end{aligned}$

不难发现, 这里的量子门的事情就是数数 (counting). 于是不难定义 $\phi$ -变换如下:

给定量子态 $|S\rangle = |s_1,\cdots,s_m\rangle$ 和 $|T\rangle = |t_1,\cdots,t_m\rangle$ , 那么对于光学网络有 $\langle T|\phi(L)|S\rangle = \frac{Per(L_{S,T})}{\sqrt{s_1!\cdots s_m!t_1!\cdots t_m!}},$ 其中 $L_{S,T}$ 去取决于光学网络和光子排布 S,T , 即 s_i 表示的第行重复 s_i 次, t_i 表示的第列重复 t_i 次. 容易观察, 令 $|S\rangle = |T\rangle = |I\rangle = |1,\cdots,1\rangle$ 的话, 可以得到 $\langle T|\phi(L)|S\rangle = Per(L)$ .

因而, 在允许延迟选择 (post-selection) 操作后, 借助上一节提及的 KLM 定理[5], 我们可以得到 Aaronson 证明中的下述定理[8]: $\frac{\Delta C}{2^n} = \langle 0\cdots 0|Q|0\cdots 0\rangle = 4^{\Gamma} \langle I|\phi(L)|I\rangle = 4^{\Gamma} Per(L_{I,I}).$ 这里的 $\Gamma$ 是量子线路中两比特门 CSIGN 门的个数. 看起来借助线性光学量子计算, 我们几乎得到了积和式是 $\mathsf{\#P}$ -complete 的新证明. 不过这里有个问题, 矩阵 $L_{I,I}$ 并不是酉矩阵. 如果我们想把结论进一步加强到对于某一类矩阵 (比如酉矩阵, 正交矩阵, 可逆矩阵等等), 应该怎么做呢?

如何处理酉矩阵

为了证明酉矩阵的积和式计算是 $\mathsf{\#P}$ -complete 的, 我们需要给 KLM 定理再增加一次编解码过程, 然后使用 KLM 定理进行规约. 具体来说, 对于单量子比特 $|1,1,1,1\rangle \rightarrow |0,1,2,1\rangle \rightarrow |1,1,1,1\rangle,$ 中间这项即是用编码矩阵编码后的新的模, 其中前两个模仍使用 dual-rail encoding, 第三个模是剩余的光子, 最后一个模则供延迟选择 (post-selection) 操作使用.

Grier-Schaeffer 的工作给出了编码矩阵对于特定类型矩阵的存在性, 可以通过求解一系列线性方程组得到; 而 CISGN 门也可以同类似方法得到, 均为域 $\mathbb{Q}(\alpha), \alpha=\sqrt{2+\sqrt{2}}+\sqrt{3+\sqrt{6}}$ 上的矩阵. 于是我们最终得到了下述定理:

给定-qubit 量子线路, 其中 CSIGN 门个数为 $\Gamma$ . 可以构造相应的 $4n+2\Gamma$ 个模上的线性光学线路, 其中是酉矩阵, 满足下式 $\frac{\Delta C}{2^n} = \langle 0\cdots 0|Q|0\cdots 0\rangle = (-\sqrt{6})^n(3\sqrt{2/3})^{\Gamma}\langle 1,\cdots,1|\phi(L) |1,\cdots, 1\rangle \propto Per(L_{I,I}).$

从而最终证明了酉矩阵的积和式计算是 $\mathsf{\#P}$ -complete 的, 基于线性光学量子计算的这一技术可以推广到其他矩阵, 甚至积和式计算的近似情形. 完整证明见 Grier-Schaefer 的工作[1], 限于笔者能力, 这里不再展开.

参考文献

[1]:[1610.04670] New Hardness Results for the Permanent Using Linear Optics

[2]:IAS 的 video archive和Scott 的 script.

[3]:[1011.3245] The Computational Complexity of Linear Optics

[4]: It from Qubits Summer School 上 Adam Bouland 的 talk (Perimeter Institute Recorded Seminar Archive)

[5]:[quant-ph/0006088] Efficient Linear Optics Quantum Computation

[6]:Harrow, Aram W., and Ashley Montanaro. "Quantum computational supremacy." Nature 549.7671 (2017): 203.

[7]:[1704.00690] Quantum advantage with shallow circuits

[8]:[1109.1674] A Linear-Optical Proof that the Permanent is #P-hard

[9]: Kogan, Grigory. "Computing permanents over fields of characteristic 3: Where and why it becomes difficult." Foundations of Computer Science, 1996. Proceedings., 37th Annual Symposium on. IEEE, 1996.

来源：知乎 www.zhihu.com
作者：Climber.pI

【知乎日报】千万用户的选择，做朋友圈里的新鲜事分享大牛。点击下载

经典网文分享

积和式, 玻色采样和计数复杂性

积和式与全同粒子

计算优越性: 玻色采样与积和式求值

经典定理的量子证明: 线性光学与新的规约技术

参考文献

没有评论:

发表评论