经典网文分享: 实分析Ⅱ|笔记整理（6）—

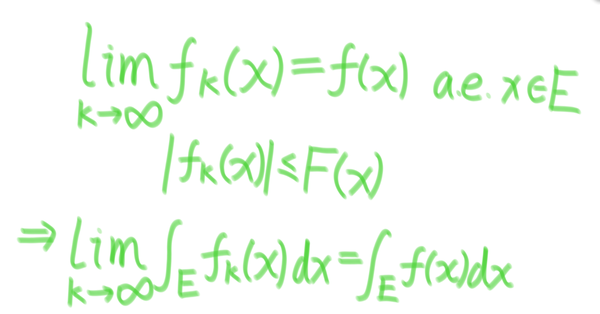
读者们好！

看了下上一篇笔记的点赞数我感觉上一篇确实是鲜有创新，所以不容易吸引人。其实本来我也想说之后都拿笔写然后再扫描进电脑，但是发现写字的话，很多话就懒得写了，那样出来的笔记，自己倒是看着还行，但是内容上和原书基本上没差……所以还是决定继续在电脑上续上这一口气了。因为电脑打字速度稍微快一些，所以还可以有时间用叙述性的语气把过程衔接起来，这样子的话笔记就会比手写要友好很多。

因为ZH5月份的bug让这一部分笔记缺失了一部分内容，具体的情况如下：

刘理：杂烩|2018.5-近期情况说明，相关typo修改

这一部分要推广上一节的积分到一般可测函数，和Stein一样，研究勒贝格积分的过程也是一步一步往外推的。

提供之前的笔记：

我们开始本节的内容。本节所含原书内容为P143-163

一般可测函数的积分

和Stein一样，讨论一般可测函数的积分的时候，我们人为的把它们分成了正部和负部。然后利用之前讨论出的结果来研究。

Definition 1:
设 $f(x)$ 为 $E \subset \mathbb{R}^n$ 上的可测函数，若积分 $\int_E f^+(x)dx,\int_E f^-(x)dx$ 中至少有一个有限值，则称 $\int_E f(x)dx=\int_E f^+(x)dx-\int_E f^-(x)dx$ 是 $f(x)$ 在 $E$ 上的积分。如果两个积分值都有限，则称它可积。并且记 $E$ 上可积函数全体为 $L(E)$ 。

同样的，因为等式 $\int_E |f(x)|dx=\int_E f^+(x)dx+\int_E f^-(x)dx$ 的存在，所以如果 $f(x)$ 可积，那么它的正部和负部都是有限的。它们的差有限，那么它们的和自然有限（或者说， $-\int_E f^{-}(x)dx$ 是有限的）。反过来推也可以，所以可以得出

$f(x),|f(x)|$ 的可积性等价。

之后我们会经常用到这个结论。

根据这个定义可以得到很多简单的性质。

Proposition 1:
(1)若 $f \in L(E)$ ，那么 $f(x)$ 在 $E$ 上几乎处处有限。
(2)若 $E \in \mathcal{U}$ ，且 $f(x)=0 ~ a.e. ~ x\in E$ ，那么 $\int_E f(x)dx=0$
(3)若 $f(x)$ 在 $E$ 上可测， $g$ 在 $E$ 上可积，且 $|f(x)| \le g(x), x \in E$ ，则 $f$ 可积。

书上在这一块添加了一个小的例子，也是一个之后可能比较多用到的结论。

Example 1:
设 $f \in L(\mathbb{R}^n)$ ，那么 $\lim_{N \to \infty}\int_{\{x \in \mathbb{R}^n: |x| \ge N\}}|f(x)|dx=0$

简单说明一下。构造 $E_N=\{x \in \mathbb{R}^n:|x| \ge N\}$ （事实上这个构造已经出现相当多次了……），那么 $\{|f(x)|\chi_{E_N}(x)\}$ 是一个渐降列。并且 $\lim_{N \to \infty}|f(x)|\chi_{E_N}(x)=0$ 。

根据这个结论和积分的相关性质，可以得到 $\lim_{N \to \infty}\int_{E_N}|f(x)|dx=\lim_{N \to \infty}\int_{\mathbb{R}^n}|f(x)|\chi_{E_N}(x)dx$ ，因为是渐降列，我们上一节介绍过这种情况积分依然是可交换的（但是成立附加了一个条件就是 $f$ 可积）。所以 $\lim_{N \to \infty}\int_{\mathbb{R}^n}|f(x)|\chi_{E_N}(x)dx=\int_{\mathbb{R}^n}\lim_{N \to \infty}|f(x)|\chi_{E_N}(x)dx=0$ ，就证明了结论。

这个定理的直观解释就是：存在一个有限集合，使得勒贝格积分在这个集合外的值可以任意小。Stein里也介绍过这个结论。

和非负可测函数的情况相同，一般情况的积分也有相似的线性性质。

Proposition 2:
若 $f,g \in L(E),C \in \mathbb{R}$ ，那么
(1) $\int_E Cf(x)dx=C \int _Ef(x)dx$
(2) $\int_E (f(x)+g(x))dx=\int_E f(x)dx+\int_E g(x)dx$

对于第一个结论。显然需要分 $C$ 的情况来进行讨论。

当 $C \ge 0$ 时，注意到 $(Cf)^+=Cf^+,(Cf)^-=Cf^-$ ，所以这种情况根据非负可测函数的线性性，第一个结论是显然的。

当 $C=-1$ 时， $(-f)^+=f^-,(-f)^-=f^+$ ，所以容易知道 $\int_E(-f(x))dx=-\int_E f(x)dx$ 。而 $C<0$ 时只需要根据 $Cf(x)=-|C|f(x)$ 即可得到结论，这里略去。

有人可能要问书上这一部分的证明为什么要加一步 $C=-1$ 的讨论。这是因为如果不加，之后的证明 $\int_E Cf(x)dx=\int_E -|C|f(x)dx=-\int_E |C|f(x)dx$ 就无法说清楚（因为我们不知道一个全负可测函数的积分是什么情况，我们只能转为非负可测函数的情况来讨论）。

再来看第二个结论。首先由 $|f(x)+g(x)| \le |f(x)|+|g(x)|$ 就可以知道 $f+g \in L(E)$ （因为这个积分绝对值是有限的）。之后，由 $(f+g)=(f+g)^+-(f+g)^-=f^+-f^-+g^+-g^-$ ，所以移项可得 $(f+g)^++f^-+g^-=(f+g)^-+f^++g^+$ 。这样的话就可以根据非负函数积分的线性性质可得 $\int_E (f+g)^+(x)dx+\int_E f^-(x)dx+\int_E g^-(x)dx=\int_E (f+g)^-(x)dx+\int_E f^+(x)dx+\int _E g^+(x)dx$

再一次移项即可得到结论。

书上在这一块举了一个与控制函数相关的例子。

Example 2:
设 $f(x)$ 是 $[0,1]$ 上的可测函数，且有 $\int_{[0,1]}|f(x)|\ln (1+|f(x)|)dx<+\infty$ ，那么 $f \in L([0,1])$ 。

这一个例子显然是想说要寻求一个 $|f(x)|$ 的控制函数。但是这里只提供了函数 $|f(x)|\ln (1+|f(x)|)$ 的可积性。显然这个函数要比 $|f(x)|$ 大，所以这就要求了 $|f(x)| \ge e-1$ 。所以可以考虑把集合按照 $|f(x)|$ 的值的范围做拆分（因为另一个部分根据测度有限，可以知道常值函数可以作这个集合上的控制函数）

设 $E_1=\{x \in [0,1]: |f(x)| \le e\},E_2=[0,1]\backslash E$ ，那么这样的话，在 $x \in E_1$ 时， $|f(x)| \le e-1$ ，在 $x \in E_2$ 时， $|f(x)| \le |f(x)| \ln (1+|f(x)|)$ 。所以在两个区间上都是可积的，那么自然在它们俩的并集上可积，就证明了结论。

这只是一个控制函数的例子，之后的控制收敛定理会系统的再讲述这一部分相关的内容。

还有一个例子，是与之前的Levi非负渐升列积分定理相关的一个结论。

Example 3:
设 $f \in L(E),f_n \in L(E)(n \in \mathbb{N})$ 。若 $\lim_{n \to \infty}f_n(x)=f(x)(x \in E),f_n(x) \le f_{n+1}(x)(n \in \mathbb{N},x \in E)$ 。那么有 $\lim_{n \to \infty}\int_E f_n(x)dx=\int_E f(x)dx$ 。

因为这是一个渐升列，所以我们和之前一样的考虑，设 $F_n(x)=f(x)-f_n(x)$ 把它改为一个渐升列。那么这样的话 $\{F_n(x)\}$ 就是 $E$ 上的非负渐降且收敛于 $0$ 的可积函数列，这样的话根据上一节的Proposition 2就可以得到 $0=\lim_{n \to \infty}\int_E F_n(x)dx=\lim_{n \to \infty}(\int_E f(x)dx -\int_E f_n(x)dx)=\int_E f(x)dx-\lim_{n \to \infty}\int_Ef_n(x)dx$ 。这就证明了结论。

这个证明可能刚开始会让人不解，因为为什么渐升列反而要转为渐降列处理。事实上是因为渐升列的性质是在非负函数下成立的。但是这里并没有非负的条件。所以只能够进行变换，转为非负函数的渐降列来处理。

好的，回到我们的主线，继续推广在非负可测函数意义下成立的性质，看看它们在一般可测函数的意义下又是否成立。

Proposition 3:
设 $E_k \in \mathcal{M}(k=1,2,\cdots),E_i \cap E_j = \emptyset(i \ne j)$ ，若 $f(x)$ 在 $E=\bigcup_{k=1}^{\infty}E_k$ 上可积，那么 $\int_E f(x)dx=\sum_{k=1}^{\infty}\int_{E_k}f(x)dx$ 。

这只需要根据 $\sum_{k=1}^{\infty}\int_{E_k}f(x)dx=\sum_{k=1}^{\infty}(\int_{E_k}f^+(x)dx-\int_{E_k}f^-(x)dx)$ $=\int_E f^+(x)dx-\int_E f^-(x)dx=\int_E f(x)dx$ 即可（因为这个性质在非负可测函数下已经证明是成立的了）。

根据这个结论容易得到

Proposition 4:
改变函数在零测集上的值不会改变它的可积性和积分值。

我们再来看一个例子。

Example 4:
设 $f(x) \in L([a,b])$ ，若对任意的 $c \in [a,b]$ 有 $\int_{[a,c]}f(x)dx=0$ ，那么 $f(x)=0 ~ a.e. x \in [a,b]$ 。

若结论不成立，那么就会存在 $E \subset [a,b],m(E)>0$ ，且 $f(x)$ 在 $E$ 上的值非零。不妨设 $E$ 上有 $f(x)>0$ 。并且取闭集 $F, F \subset E$ ，且有 $m(F)>0$ ，令 $G=(a,b) \backslash F$ ，就有 $\int_G f(x)dx+\int_F f(x)dx=0$ 。

根据 $\int_F f(x)dx>0$ 可得 $\sum_{n \ge 1} \int_{[a_n,b_n]}f(x)dx=\int_G f(x)dx \ne 0$ （ $[a_n,b_n]$ 是开集的构成区间，事实上 $a_n,b_n$ 都取成有理数即可）。那么就有 $\int_{[a_{n_0},b_{n_0}]}f(x)dx \ne 0$ 对于某一个 $n_0$ 成立。但是另一方面， $\int_{[a,a_{n_0}]}f(x)dx =0,\int_{[a,b_{n_0}]}f(x)dx =0$ ，所以这就与上面的结论矛盾了。

接下来引入的是积分的绝对连续性和平移变换定理。

Proposition 5:
设 $f \in L(E)$ ，那么对于任意的 $\epsilon>0$ ，存在 $\delta>0$ ，使得当 $E$ 中子集 $e$ 的测度 $m(e)<\delta$ 时有 $|\int_e f(x)dx| \le \int_e |f(x)|dx < \epsilon$

不妨设 $f(x) \ge 0$ ，那么根据简单函数逼近定理和非负渐升列积分定理可得，对任意的 $\epsilon>0$ ，存在可测简单函数 $\varphi(x),0 \le \varphi(x) \le f(x)(x \in E)$ ，使得 $\int_E (f(x)-\varphi(x))dx=\int_E f(x)dx-\int_E \varphi(x)dx<\epsilon/2$ 。

注意到 $f(x)=(f(x)-\varphi(x))+\varphi(x)$ ，所以只需要考虑 $\varphi(x)$ 在区间上的积分即可。这里我们设 $\varphi(x) \le M,\delta=\epsilon/(2M)$ ，根据 $\int_ef(x)dx\le \int_E (f(x)-\varphi(x))dx+\int_e \varphi(x)dx \le \epsilon$ 即可得到结论。

Proposition 6:
若 $f \in L(\mathbb{R}^n)$ ，那么对于任意的 $y_0 \in \mathbb{R}^n,f(x+y_0) \in L(\mathbb{R}^n)$ ，有 $\int_{\mathbb{R}^n}f(x+y_0)dx=\int_{\mathbb{R}^n}f(x)dx$ 。

根据积分的定义知只需要考虑 $f(x) \ge 0$ 的情况。我们一步步来推，先考虑非负可测简单函数的情况。

设 $f(x)=\sum_{i=1}^{k}c_i \chi_{E_i}(x) , x \in \mathbb{R^n}$ ，这样的话， $f(x+y_0)=\sum_{i=1}^{k}c_i\chi_{E_i-\{y_0\}}(x)$ 仍然是非负可测简单函数。所以根据 $m(E_i-\{y_0\})=m(E_i)$ 即可得到 $\int_{\mathbb{R}^n}f(x+y_0)dx=\int_{\mathbb{R}^n}f(x)dx$ 。

如果是一般非负可测函数，那么存在非负可测简单函数渐升列 $\{\varphi_k(x)\}$ ，使得 $\lim_{k \to \infty}\varphi_k(x)=f(x),x \in \mathbb{R}^n$ 。那么自然可知 $\{\varphi_k(x+y_0)\}$ 仍然为渐升列。并且 $\lim_{k \to \infty}\varphi_k(x+y_0)=f(x+y_0),x \in \mathbb{R}^n$ 。所以由非负函数渐升列积分定理可得 $\int_{\mathbb{R}^n}f(x+y_0)dx=\lim_{k \to \infty}\int_{\mathbb{R}^n}\varphi_k(x+y_0)dx=\lim_{k \to \infty}\int_{\mathbb{R}^n}\varphi_k(x)dx=\int_{\mathbb{R}^n}f(x)dx$ ，这就证明了结论。

这个证明方法运用的结论都是在测度部分所证明的。测度部分的结论告诉我们，对点集做平移和伸缩变换，其测度也会对应的变化（平移变换不变，伸缩变换会使测度对应收缩）。

运用同样的方法，我们再来看书上的这一个例子（不得不说这一节书上的例子我得抄挺多的……）。

Example 5:
设 $I \subset \mathbb{R}$ 是区间， $f \in L(I)$ ， $a \ne 0$ ，记 $J=\{x/a: x \in I\}$ ， $g(x)=f(ax)(x \in J)$ ，则 $g \in L(J)$ ，并且有 $\int_Lf(x)dx=|a|\int_Lg(x)dx$ 。

还是一样，先讨论简单可测函数的情况。

先设 $f(x)=\chi_E(x)$ ，其中 $E$ 是 $I$ 中的可测集，那么 $a^{-1}E \subset J$ 。又 $\chi_E(ax)=\chi_{a^{-1}E}(x)$ ，所以有 $\int_Jg(x)dx=\frac1{|a|}m(E)=\frac1{|a|}\int_If(x)dx$ ，同理可以推出简单可测函数的情况。

再讨论一般情况。设简单可测函数列 $\{\varphi_n(x)\}$ 满足 $\varphi_n(x) \to f(x)(n \to \infty,x \in I)$ ，并且 $|\varphi_n(x)| \le |f(x)|$ 。再令 $\psi_n(x)=\varphi_n(ax)$ ，那么 $\varphi_n(x) \to g(x)$ 并且也是简单函数列。所以有 $|a| \int_Jg(x)dx=|a| \lim_{n \to \infty}\int_J \psi_n(x)dx=\lim_{n \to \infty} \int_I \varphi_n(x)dx=\int_I f(x)dx$ 。

控制收敛定理

这是勒贝格积分理论中最重要的结果之一。

Theorem 1:
设 $f_k \in L(E)(k=1,2,\cdots)$ ，并且有 $\lim_{k \to \infty}f_k(x)=f(x) ~ a.e. ~ x \in E$ 。若存在 $E$ 上可积函数 $F(x)$ 使得 $|f_k(x)| \le F(x) ~ a.e. ~ x \in E(k=1,2,\cdots)$ ，那么就有 $\lim_{k \to \infty} \int _E f_k(x)dx=\int_E f(x)dx$ 。

首先，根据 $|f(x)| \le F(x) ~a.e. x \in E$ 可知 $f(x)$ 为 $E$ 上可积函数，那么作函数列 $g_k(x)=|f_k(x)-f(x)|$ ，那么 $g_k \in L(E), 0 \le g_k(x) \le 2 F(x) ~ a.e. ~ x \in E$ 。

首先运用Fatou引理可得 $\int_E \lim_{k \to \infty}(2F(x)-g_k(x))dx \le \underline{\lim}\limits_{k \to \infty}\int_E (2F(x)-g_k(x))dx$ 。那么稍微放缩一下可得 $\int_E 2F(x)dx-\int_E \lim_{k \to \infty}g_k(x)dx \le \int _E 2F(x)dx-\overline{\lim}\limits_{k \to \infty}\int_E g_k(x)dx$ 。由 $\lim_{k \to \infty}\int_Eg_k(x)dx=0$ ，在不等式中消去两边的 $\int_E 2F(x)dx$ ，可得 $\overline{\lim}\limits_{k \to \infty}\int_E g_k(x)dx =0$ 。最后根据 $|\int_E f_k(x)dx-\int_E f(x)dx| \le |\int_E (f_k(x)-f(x))dx| \le \int_E g_k(x)dx$ 可知定理结论成立。

当然了，控制收敛定理也绝非只有这一种形式。下面这个被称为依测度收敛的控制收敛定理。

Theorem 2:
设 $f_k \in L (\mathbb{R}^n)(k=1,2,\cdots)$ ，且 $f_k(x)$ 在 $\mathbb{R}^n$ 上依测度收敛于 $f(x)$ 。若存在 $F \in L(\mathbb{R}^n)$ ，使得 $|f_k(x)| \le F(x) (k=1,2,\cdots; a.e. ~ x \in \mathbb{R}^n)$ 。那么 $f \in L ( \mathbb{R}^n)$ ，并且有 $\lim_{k \to \infty}\int_{\mathbb{R}^n} f_k(x)dx=\int_{\mathbb{R}^n}f(x)dx$ 。

这个证明方法是比较麻烦的。但是按照书上的说法，"习之也不无益处"。

设 $\epsilon>0$ 任意给定，则只需要说明存在 $K$ ，使得 $k>K$ 时有 $\int_{\mathbb{R}^n}|f_k(x)-f(x)|dx < \epsilon$ 即可。

首先根据Riesz定理（原书定理的3.17，这一部分没有笔记），存在 $\{f_{k_i}(x)\}$ 使得 $\lim_{i \to \infty}f_{k_i}(x)=f(x) ~ a.e. ~ x\in \mathbb{R}^n$ 。也就是说 $|f(x)| \le F(x) ~ a.e. ~ x\in \mathbb{R}^n$ 。

其次，我们对函数做一些定义域的划分，以化简讨论。

首先根据Example 1可知存在 $N$ 使得 $\int_{\{x : |x| \ge N\}}F(x)dx < \epsilon /6$ 。那么自然可以得到 $\int_{\{x: |x| \ge N\}}|f_k(x)-f(x)|dx\le2\int_{\{x : |x| \ge N\}}F(x)dx <\epsilon/3$ 。

其次，根据积分连续性(Proposition 5)，可得存在 $\delta>0$ ，使得 $m(e) < \delta$ 时有 $\int_e F(x)dx < \epsilon /6$ 。所以 $\int_e |f_k(x)-f(x)|dx \le 2 \int_e F(x)dx < \epsilon/3$ 。所以根据这个结论，我们考虑取满足这个条件的集合 $e$ 。注意到 $f_k(x)$ 依测度收敛于 $f(x)$ ，所以我们设 $B=B(0,N),m(B)=l,E_k=\{x \in B: |f_k(x)-f(x)| > \epsilon/(3l)\}$ 。（显然，我们现在关注的问题就是 $|x| \le N$ 这一部分区域的情况）这个时候就一定会存在 $K$ ，使得 $k \ge K$ 时有 $m(E_k)<\delta$ 。

最后，我们讨论 $k \ge K$ 情况下的积分区域。分解定义域为两块。一部分是 $\{x: |x| \ge N\}$ ，这一块的函数积分一定是 $< \epsilon/3$ 的。然后下面讨论 $\int_B|f_k(x)-f(x)|dx$ ，分解为 $\int_{E_k}|f_k(x)-f(x)|dx+\int_{B \backslash E_k}|f_k(x)-f(x)|dx$ 。那么有一部分积分是小于 $\epsilon/3$ 的。还有一部分，注意到 $x \in B \backslash E_k$ 时， $|f_k(x)-f(x)| \le \epsilon/(3l)$ 。所以 $\int_{B \backslash E_k}|f_k(x)-f(x)|dx \le \int_B \epsilon/(3l)dx=\epsilon/3$ 。三块合在一起就可以得到我们想要的结论。

可以看出来，这个证明虽然麻烦，但是逻辑清晰，思维缜密（有点像书上的定理3.9，也就是简单可测函数逼近定理）。所以如果能够多看几遍，其实也就相当于过了一遍之前已经学过的几个定理和性质了。

最后我们以它的两个重要的推论结束这一章。

Corollary 1:
设 $f_k \in L(E)$ ，若 $\sum_{k =1}^{\infty}\int_E |f_k(x)|dx < +\infty$ ，那么 $\sum_{k=1}^{\infty}f_k(x)$ 在 $E$ 上几乎处处收敛。若记其和函数为 $f(x)$ ，那么 $f \in L(E)$ ，并且有 $\sum_{k=1}^{\infty}\int_E f_k(x)dx=\int_E f(x)dx$ 。

（这一部分Stein也证明过，但是证明的视角不太相同）

首先我们作 $F(x)=\sum_{k=1}^{\infty}|f_k(x)|$ ，那么由非负可测函数的积分定理（上一节的Theorem 6）可得 $\int_E F(x)dx=\sum_{k=1}^{\infty}\int_E |f_k(x)|dx < +\infty$ 。这样的话 $F$ 就是可积的。这就推出了 $F$ 几乎处处有限，那就说明级数几乎处处收敛，设和函数为 $f(x)$ ，则由 $|f(x)| \le \sum_{k=1}^{\infty}|f_k(x)| =F(x)$ 可知 $f(x)$ 可积。设 $g_m(x)=\sum_{k=1}^{m}f_k(x)$ ，类似方法可以推出它可积。所以根据控制收敛定理可得 $\int_E f(x)dx=\int_ E \lim_{m \to \infty}g_m(x)dx=\lim_{m \to \infty}\int_E g_m(x)dx=\sum_{k=1}^{\infty}\int_E f_k(x)dx$ （强调一下，控制收敛定理得到的一个最重要的结论就是积分和极限可交换），这就证明了结论。

不难看出，这就是推广了之后的逐项积分定理。

Corollary 2:
设 $f(x,y)$ 是定义在 $E \times (a,b)$ 上的函数，它作为 $x$ 的函数在 $E$ 上可积，作为 $y$ 的函数在 $(a,b)$ 上可微。若存在 $F \in L(E)$ ，使得 $|\frac{d}{dy}f(x,y)| \le F(x)$ ，那么 $\frac{d}{dy}\int_E f(x,y)dx=\int_E \frac d{dy}f(x,y)dx$ 。