经典网文分享: 物理中的因果性-线性因果系统

在这个问题下

日常怼张工的活动刚刚落下了帷幕，留下一地鸡毛。但其实中文网络上少有讲为什么从波动方程出发可以导致信号传递速度低于光速这件事。那么这里我计划通过两到三篇文章，从物理学家常用的视角谈谈因果性这件事。当然这件事在量子场论中也有不少应用，例如光学定理、费曼图的解析行为等等，本人水平有限，可能最后会稍微提一句。

第一篇谈最简单的情形，我们在线性非时变系统的框架下，讨论如何去描述，只能是过去的原因导致未来的结果这件事。这个东西在信号与系统中叫做因果系统。

本文假定读者具有复变函数相关的基础知识。

假定系统具有输入信号 $A$ 和输出信号 $B$ 。他们可以是单口电路网络中的电压与电流，或者双端口网络中两端的信号。考虑到系统是线性非时变的，那么如果我输入稳态的一个单频信号 $A(t) = \tilde A(\omega)\mathrm e^{\mathrm i\omega t}$ ，出来的也一定是单频信号 $B(t) = \tilde B(\omega)\mathrm e^{\mathrm i\omega t}$ ，且两个信号幅值之间满足一个线性关系

$\tilde B(\omega) = X(\omega)\tilde A(\omega)$

其中 $X(\omega)$ 是某个与频率相关的系数，称为响应函数。接下来我们就要把注意力放在这个东西上面。

我们尤其关心的是 $X(\omega)$ 取无穷大值的地方，这意味着只需要无穷小的输入信号便可以激发有限的输出信号。这意味着什么呢？我们来看两个例子：

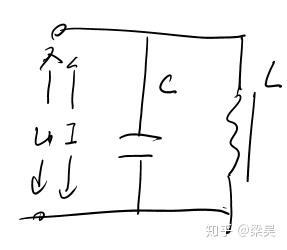
我们取外电流为输入信号，外电压为输出信号。有关系

$U(\omega)=\frac{I(\omega)}{\mathrm i\omega C+\frac{1}{\mathrm i\omega L}}$

那么响应函数为

$\tilde X(\omega) = \frac{\mathrm i\omega L}{1-\omega^2LC}$

显然，当 $\omega = \pm1/\sqrt{LC}$ 时，响应函数变为无穷大。我们容易注意到，这个频率恰好是LC谐振电路发生谐振的频率——不需要外界的电流输入，电路本身就能以这个频率震荡。也就是说，响应函数发散的点对应着系统内部的共振频率。

此外，响应函数也可能会在 $\omega$ 取复值时发散。我们看第二个例子

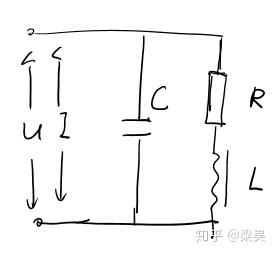
电路中外加了一个电阻R，这样响应函数写作

$\tilde X(\omega) = \frac{R+\mathrm i\omega L}{1-\omega^2LC+\mathrm i\omega RC}$

此时响应函数发散，也即分母为零的点变为

$\omega = \mathrm i\frac{R}{2L}\pm\sqrt{\frac{1}{LC}-\left(\frac{R}{2L}\right)^2}$

成了一个复数，我们可以注意到有 $\mathrm{Im}\, \omega>0$ 。

以一个复数频率震荡是什么意思？我们不妨明确的写出对时间依赖的式子

$B(t) =\tilde B(\omega) \mathrm e^{\mathrm i\text{Re}\,\omega t}\mathrm e^{-\text{Im}\,\omega t}$

这样，我们得到的便是一个随时间衰减的震荡，或者说阻尼震荡的结果。

另外，从这里可以知道， $\text{Im}\,\omega\ge 0$ 这个结果并不是特例，而是一个普遍性的结论——我们显然不期望看到一个系统在没有任何激励的情况下，振幅越来越大直至发散。

我们把这样响应函数发散的点称为它的极点，那么上面所讨论的结论便可记作：响应函数的全部极点分布在复平面的上半平面上。

这个结论可以给我们什么进一步结果吗？下面便来看看：

现在考虑输入信号并不仅仅是单频波，而是一般性的组合

$A(t) = \int\tilde A(\omega)\mathrm e^{\mathrm i\omega t}\,\mathrm d\omega$

那么可以相应的给出输出信号

$B(t) = \int\tilde X(\omega)\tilde A(\omega)\mathrm e^{\mathrm i\omega t}\,\mathrm d\omega$

利用卷积定理，我们有

$B(t)=\int_{-\infty}^{\infty} X(\tau)A(t-\tau)\,\mathrm d\tau$

这里 $X(\tau)$ 是相应的傅里叶变换

$X(\tau) = \int_{-\infty}^{\infty}\tilde X(\omega)\mathrm e^{\mathrm i\omega \tau}\,\mathrm d\omega$

我们考虑如何通过围道积分的办法来求这个积分。对于 $\tau>0$ 的情形，我们可以为这个实轴上的积分补上一个上半圆周成为一条闭合回路。由于指数因子的压低，上半圆周的积分值为零，从而考虑整条围道的积分即可。而围道的积分又等于围道内的全部极点的留数之和，这样我们便知道被积函数有一个非零值。

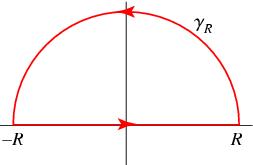
对于 $\tau<0$ 的情形，我们就必须补上一个下半圆周了。考虑到下半平面上没有极点，就没有所谓的留数之和，那么这个积分便为零。我们便得到

$X(\tau<0)=0$

进而输出信号与输入信号的关系为

$B(t) = \int_0^\infty X(\tau)A(t-\tau)\,\mathrm d\tau$

这样，我们得到了一个非常重要的结论：某一时刻 $t$ 输出信号是多少，仅取决于此时刻之前（ $t-\tau<t$ ）的输入信号，而与此时刻之后的输入信号无关。换句话说，原因总在结果之前！

总结一下，我们以傅里叶变换和留数定理作为桥梁，证明了对于线性系统而言，孤立系统的运动总是自发衰减，与原因总在结果之前，这两件看上去毫无关联的事情完全是等价的。同时我们也提供了一个描述线性激发-响应过程的一般性工具。

下一篇文章中，我们将在时间之外引入空间的维度，讨论波的传播。

来源：知乎 www.zhihu.com
作者：梁昊

【知乎日报】千万用户的选择，做朋友圈里的新鲜事分享大牛。点击下载

经典网文分享

物理中的因果性-线性因果系统

没有评论:

发表评论