经典网文分享: 如何用 C 语言画小猪佩奇

我们曾在《用 C 语言画光（一）：基础》中，使用到带符号距离场（signed distance field, SDF）表示圆形：

$\phi_\text{circle}(\mathbf{x})=\| \mathbf{x} - \mathbf{c}\| - r\tag{1}$

沿用这个方法表示形状，但这次我们想利用 ASCII 字符|/=\画出形状的外框，并填充内部，类似这样：

   =====   //.....\\  ||.......||   \\.....//     =====

SDF 的梯度（gradient）代表 SDF 变化最大的方向，可用这个方向去决定用哪一个字符。

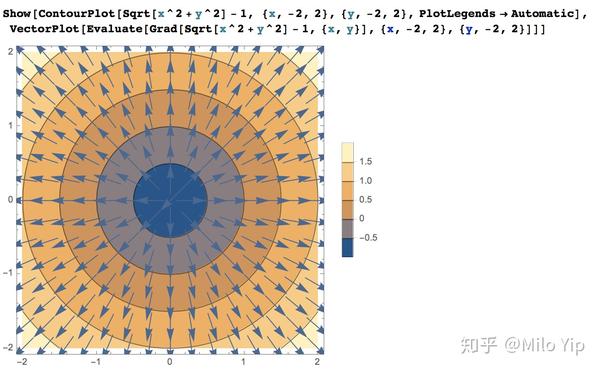
我们通过差分求 SDF 的梯度近似值，然后用 atan2() 求出梯度的角度：

$\begin{align} \theta &= \mathrm{atan2} \left(\frac{\partial \phi(\mathbf{x})}{\partial y}, \frac{\partial \phi(\mathbf{x})}{\partial x} \right) \tag{2}\\ &\approx \mathrm{atan2} \left(\phi(x,y+\Delta) - \phi(x,y-\Delta), \phi(x+\Delta,y) - \phi(x-\Delta,y)\right) \tag{3}\\ \end{align}$

用 C 语言简单实现，在 $[-1, 1]\times[-1,1]$ 画布中画一个半径 0.8 并带有 0.1 寛度外框的圆形：

#include <math.h>  #include <stdio.h>  #define T double    T f(T x, T y) {      return sqrt(x * x + y * y) - 0.8f;  }    char outline(T x, T y) {      T delta = 0.001;      if (fabs(f(x, y)) < 0.05) {          T dx = f(x + delta, y) - f(x - delta, y);          T dy = f(x, y + delta) - f(x, y - delta);          return "|/=\\|/=\\|"[(int)((atan2(dy, dx) / 6.2831853072 + 0.5) * 8 + 0.5)];      }      else if (f(x, y) < 0)          return '.';      else          return ' ';  }    int main() {      for (T y = -1; y < 1; y += 0.05, putchar('\n'))          for (T x = -1; x < 1; x += 0.025)              putchar(outline(x, y));  }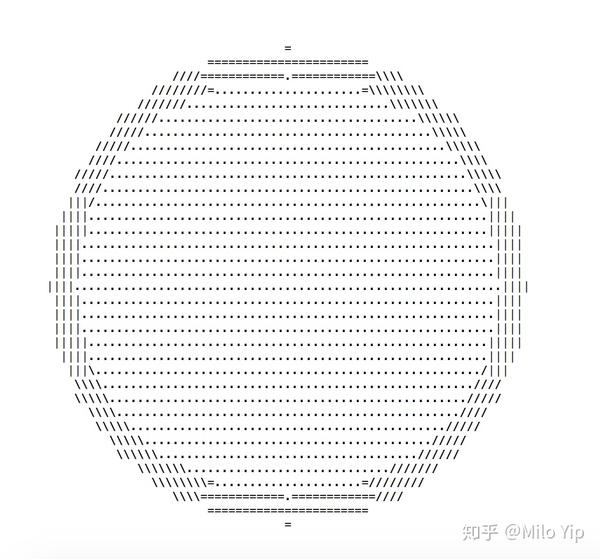

然后，我们就可以画多个圆形，把它们适当地旋转和缩放，用构造实体几何比它们组合起来，那么用19行代码就可以画出小猪佩奇了：

// ASCII Peppa Pig by Milo Yip  #include <math.h>  #include <stdio.h>  #include <stdlib.h>  #define T double  T c(T x,T y,T r){return sqrt(x*x+y*y)-r;}  T u(T x,T y,T t){return x*cos(t)+y*sin(t);}  T v(T x,T y,T t){return y*cos(t)-x*sin(t);}  T fa(T x,T y){return fmin(c(x,y,0.5),c(x*0.47+0.15,y+0.25,0.3));}  T no(T x,T y){return c(x*1.2+0.97,y+0.25,0.2);}  T nh(T x,T y){return fmin(c(x+0.9,y+0.25,0.03),c(x+0.75,y+0.25,0.03));}  T ea(T x,T y){return fmin(c(x*1.7+0.3,y+0.7,0.15),c(u(x,y,0.25)*1.7,v(x,y,0.25)+0.65,0.15));}  T ey(T x,T y){return fmin(c(x+0.4,y+0.35,0.1),c(x+0.15,y+0.35,0.1));}  T pu(T x,T y){return fmin(c(x+0.38,y+0.33,0.03),c(x+0.13,y+0.33,0.03));}  T fr(T x,T y){return c(x*1.1-0.3,y+0.1,0.15);}  T mo(T x,T y){return fmax(c(x+0.15,y-0.05,0.2),-c(x+0.15,y,0.25));}  T o(T x,T y,T(*f)(T,T),T i){T r=f(x,y);return fabs(r)<0.02?(atan2(f(x,y+1e-3)-r,f(x+1e-3,y)-r)+0.3)*1.273+6.5:r<0?i:0;}  T s(T x,T y,T(*f)(T,T),T i){return f(x,y)<0?i:0;}  T f(T x,T y){return o(x,y,no,1)?fmax(o(x,y,no,1),s(x,y,nh,12)):fmax(o(x,y,fa,1),fmax(o(x,y,ey,11),fmax(o(x,y,ea,1),fmax(o(x,y,mo,1),fmax(s(x,y,fr,13),s(x,y,pu,12))))));}  int main(int a,char**b){for(T y=-1,s=a>1?strtod(b[1],0):1;y<0.6;y+=0.05/s,putchar('\n'))for(T x=-1;x<0.6;x+=0.025/s)putchar(" .|/=\\|/=\\| @!"[(int)f(u(x,y,0.3),v(x,y,0.3))]);}