经典网文分享: 【CFT01】度规初步

本学期参加了一个共形场论的研讨班，为了变成一个合格的名词党所以做一些相关的读书笔记。本文主要介绍了微分流形以及度规张量的概念，以及举了一些常见的例子，用以为后续的讨论的共形场论提供数学基础。本系列主要参考Paul Ginsparg的应用共形场论教材[1]，本文还参考了梁灿彬的广相教材[2]。

我们先复习微分流形的概念。直观上，我们研究一个光滑的空间，其任意小邻域都和欧氏空间类似。数学上，一个 $C^\infty$ 微分流形是一个（维的）拓扑空间，其满足：

其是Hausdorff空间，即任意两点可被它们的邻域分离；
存在维局部坐标邻域（在拓扑上是开集），即对任意给定流形上的点，存在其的一个邻域和一个映射 $\varphi: U\rightarrow U'$ （这里是 $\mathbb R^n$ 上的一个开集），使得 $\varphi$ 是同胚（连续双射且反函数连续），另外有序对族 $\{(U_\alpha,\varphi_\alpha)\}$ 被称为该流形的图册（atlas）, $\alpha$ 被称为索引；
其图册的转移映射（transition map）是光滑的，如图所示， $U_\alpha$ 和 $U_\beta$ 是两个有重叠部分的开集，它们分别同胚于 $\mathbb R^n$ 上的开集，而重叠部分在 $\mathbb R^n$ 上的两个像之间的映射 $\varphi_{\alpha\beta}$ （或其逆映射 $\varphi_{\beta\alpha}$ ）叫转移映射。

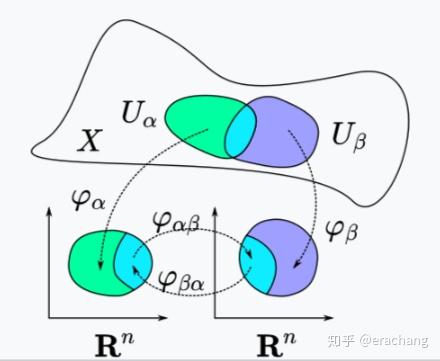
最简单的微分流形就是 $\mathbb R^m$ 本身，黎曼球面 $\mathbb S^2$ 也是常见的微分流形。直观上一个微分流形可以嵌入到一个更高维的欧几里得空间中，而对于流形上的一点，在其上和流形相切的欧几里得子空间即其切空间（tangent space）。

然而基于更高维平直空间嵌入的定义方式并不是最好的定义切空间的方式。为了定义流形上的切空间，我们先观察 $\mathbb R^n$ 上的向量，其具有长度、方向，但这些概念很难在流形上推广。注意到若 $\mathbf v$ 是一个向量，则对于任意函数 $f:\mathbb R^n\rightarrow \mathbb R$ ，让其在一点上沿 $\mathbf v$ 方向上求导，其导函数值等于某个实数。故 $\mathbf v$ 是 $\mathbb R^n$ 上所有光滑函数的集合到实数的映射，且其服从线性和莱布尼兹率。

【切空间】称 $f:M\rightarrow \mathbb R$ 是流形上的一个 $C^\infty(M)$ 函数，若对于每组 $\{U,\varphi\}$ 都有 $f\circ\varphi^{-1}: \varphi(U)\rightarrow \mathbb R$ 是光滑的。对于 $x\in M$ ，称映射 $\partial:C^\infty(M)\rightarrow \mathbb R$ 为上的导数，若其满足莱布尼兹率即 $\partial(fg)=\partial(f)g+f\partial(g)$ 。如果再者我们定义导数的加法和数乘满足线性，即 $(\lambda \partial_1+\partial_2)(f)=\lambda \partial_1(f)+\partial_2(f)$ ，我们则有一个由所有导数组成的线性空间，称处的切空间。

对于一个光滑流形上一点，其邻域上有映射 $\varphi=(x^1,\cdots,x^n):U\rightarrow \mathbb R^n$ ，其中 $(x^1,\cdots,x^n)$ 是一组 $\mathbb R^n$ 的基底，则可以对应地在切空间 T_xM 上定义一组基底 $(\partial_{x^1},\cdots,\partial_{x^n})$ 满足

$\partial_{x^i}(f)\Big|_{x}:=(\partial_{i}(f\circ\varphi^{-1}))(\varphi(x)),\forall f\in C^\infty(M)\\$ 即对对应的 $\mathbb R^n$ 上的光滑函数在第个分量（即方向 x^i 上）求导，那么对于任意的切向量我们可以找到一组线性组合满足 $v=\sum_iv_i\partial_{x^i}$ 。

为了研究微分流形的距离结构，我们需要研究其线元素（或称第一基本形）。直观的理解是流形上一点附近的一段微小的长度（的平方），即欧几里得平面上的 $\Delta s^2=\Delta x^2+\Delta y^2$ 。我们可以考虑将每个方向上的微元放缩一个倍数，比如 $\Delta s^2=\Delta x^2+1/2\Delta y^2$ ，即在轴上的距离变化比轴上的距离变化"更短"，这类似于一个圆柱面。于是，对于非欧的流形上的推广，我们希望将线元素定义为 $\mathrm dx^2_i$ 的线性组合，"尽可能不"出现交叉项 $\mathrm dx\mathrm dy$ ，又或者考虑变换坐标系对其的影响等。

我们的动机是需要构造形如 $\mathrm ds^2=\sum_i a_i\mathrm dx_i^2$ 的量，则需定义度规张量（metric tensor，或简称度规）来定义上述的 a_i 。形式化的理解度规是对"给定坐标的" 维微分流形上，每一点都对应的一个 $n\times n$ 的对称、满秩的矩阵，该矩阵可以描述该点附近空间的距离结构。严谨的定义如下：

【度规张量】是微分流形，是其上的一点，其切空间为 $\mathrm T_xM$ 。上的一个度规张量 $g_x:\mathrm T_xM\times\mathrm T_x M\rightarrow \mathbb R$ ，将两个切向量映到实数，且满足：
1. 双线性，即等；
2. 对称性，；
3. 非退化性， $\forall X\ne 0, \exists Y \text{ s.t. }g(X,Y)\ne 0$ 。
另外我们还要求是光滑变化的，即对于给定邻域内的光滑向量场和，关于光滑。

注意到有限维线性空间上的双线性映射都可以由矩阵描述，故度规也可以由矩阵给出表述。

为了方便我们先引入简化记号 $\mathbf a\cdot\mathbf b =a_jb^j=\sum_{j=1}^na_jb^j$ ，这里上标不是指数而是标号。

现在假设我们在切空间上有一组基 $\mathbf e=(e_1,\cdots ,e_n)$ （ $\mathbf e$ 是一个 $n\times n$ 的矩阵），则我们定义 $g_{ij}[\mathbf e]=g(e_i,e_j)$ ，其构成一个 $n\times n$ 的矩阵，记为 $G[\mathbf e]$ 。假设另外有两个向量 v=v^ie_i, w=w^ie_i （意为列向量 $(v^1,\cdots,v^n)^\top$ 和 $(w^1,\cdots,w^n)^\top$ ），由双线性我们有 $g(v,w)=v^iw^jg_{ij}[\mathbf e]$ ，写成向量和矩阵的形式即 $g(v,w)=v^\top Gw=w^\top Gv$ 。同理对于线性变换 $\mathbf e\rightarrow \mathbf eA$ ，度规的变换为 $G[\mathbf e A]=A^\top G[\mathbf e]A$ 。注意到由于上述向量都是切向量，即 $\mathbf e=\left(\partial_{x^1},\cdots,\partial_{x^n}\right)$ ，故线性变换实际上是雅可比矩阵，即 $a_{ij}=\partial_{x^i}y^j$ 。另外，由对称性可知矩阵是对称的，由非退化性可知 $\det G\ne 0$ 。

度规具有矩阵结构这个性质可以很方便地让我们研究其上的各种性质，对称性允许我们对其求特征值，非退化性保证了特征值不为0，进而定义度规的符号（signature）：

【符号】（满秩）矩阵的符号为一个二元组，分别代表其正负特征值的个数。

注意到符号具有旋转不变性，即不取决于基的选择，故可以定义度规（在一点处）的符号数。另外度规的符号实际上是某种广义对流形的衡量：

若是单连通的，其度规的符号不取决于点的选择。

对于单连通的微分流形，若的符号是 (n,0) ，我们称该流形为黎曼流形，否则称为伪黎曼流形。一个重要的伪黎曼流形的例子是洛伦兹流形，其符号为 (p,1) 。通常在物理上，我们把看成类空维度，看成类时维度，另外如果是退化的，我们把特征值等于0的维度称为类光维度。

现在线元素（line element）或者其平方第一基本形（first fundamental form）可以被定义为：

$\mathrm ds^2=g_{ij}\mathrm dx^i\mathrm dx^j$ 。

我们总是可以对度规张量求特征值，使得第一基本形不包含交叉项，即若的特征值是 $\{\lambda_i\}$ 则 $\mathrm ds^2=\sum_i\lambda_i\mathrm dx^2_i$ ，即直观理解将每个方向上的"长度"放缩了一个倍数。则可知对流形上的一条曲线，对其参数做积分即可求得其长度，即 $L_{ab}=\int_{a}^b\sqrt{\mathrm ds^2}$ 。故此，我们说度规张量描述了流形的距离结构。再者，我们可以用度规定义体积形式（volume form）：

$\omega=\sqrt{|\det g|}\,\mathrm dx^1\wedge\cdots\wedge\mathrm dx^n$

直观上理解假如我们将基底正交化为的特征向量方向，则变成一个对角阵，则体积形式简化成 $\prod_i\sqrt{\lambda_i}\bigwedge_i\mathrm dx^i$ ，这与欧氏空间的体积微元定义相符 $\prod_{i}\Delta x^i$ ，区别是在每个方向上做了放缩。另外任何体积形式都定义了该空间上的一个波莱尔测度 $\mu(U)=\int_U\omega$ ，但进一步为了定义波莱尔测度我们不需要流形的连续性和光滑性。

下面我们来讨论一些例子：

二维欧几里德流形。在笛卡尔坐标系下其度规为单位矩阵，对应的线元素为 $\mathrm ds^2=\mathrm dx^2+\mathrm dy^2$ 。若我们把坐标变换成极坐标系，度规 $g=J^\top J=\mathrm{diag}(1,r^2)$ 其中是雅可比矩阵，即 $\mathrm ds^2=\mathrm dr^2+r^2\mathrm d\theta^2$ 。
四维洛伦兹流形。线元素是 $\mathrm ds^2=\mathrm dx^2+\mathrm dy^2+\mathrm dz^2-c^2\mathrm dt^2$ ，其中是光速，其有三个类空维度和一个类时维度。若将它转换成球面坐标我们有 $\mathrm ds^2=-c^2\mathrm dt^2+\mathrm dr^2+r^2\mathrm d\Omega^2$ 其中 $\mathrm d\Omega^2=\mathrm d\theta^2+\sin^2\theta\mathrm d\phi^2$ ，后者是 $\mathbb S^2$ 上的一个标准度量。计算并不复杂，我们写出 $\mathbb R^3$ 中球坐标变换公式 $x=r\sin\theta\sin\phi\\y=r\sin\theta\cos\phi\\z=r\cos\theta$ 然后对其求雅可比矩阵 $J=\frac{\partial(x,y,z)}{\partial(r,\theta,\phi)}$ ，则 $G=J^\top J$ ，我们用Mathematica辅助计算易得结果 $\mathrm ds^2=\mathrm dr^2+r^2(\mathrm d\theta^2+\sin^2\theta\mathrm d\phi^2)$ 。最后需要把空间限制在单位球面上，即对 $\delta(r^2-1)$ 做积分得 $\mathrm d\Omega^2$ 。

JacobianMatrix[f_List?VectorQ, x_List] :=   Outer[D, f, x] /; Equal @@ (Dimensions /@ {f, x})(*define Jacobian matrix*) cartesian = {r*Sin[t] Cos[p], r*Sin[t] Sin[p], r*Cos[t]}; sphere = {r, t, p}; J = JacobianMatrix[cartesian, sphere]; FullSimplify[MatrixForm[Transpose[J].J]]

我们有3维得欧几里德空间得（平直）度量，用极坐标表示为 $\mathrm ds^2=\mathrm dr^2+r^2\mathrm d\Omega^2$ 。对于 $\mathbb S^3$ ，我们将其嵌入 $\mathbb R^4$ 并考虑其坐标 $(R,r,\theta,\phi)$ ，其中后三个分量是一个三维球坐标，描述了子空间 $\mathbb R^3$ ，而是该四维向量的长度，则坐标变换如上述的球坐标以及第四个分量 $w=\sqrt{1-r^2}$ ，然后把它们缩放倍，则求得该坐标下的度量为 $\mathrm{diag}(1,R^2/(1-r^2),r^2R^2,r^2R^2\sin^2\theta)$ ，最后对delta函数 $\delta(R^2-1)$ 做积分我们有度量 $\mathrm ds^2=\frac{1}{1-r^2}\mathrm dr^2+r^2\mathrm d\Omega^2$ 。类似地我们考虑三维马鞍面，将其嵌入伪欧几里得空间 $\mathbb R^4$ 中，度量为 $\mathrm ds^2=\mathrm dx^2+\mathrm dy^2+\mathrm dz^2-\mathrm dw^2$ ，类似地考虑变量代换 $(x,y,z,w)\rightarrow(R,r,\theta,\phi)$ ： $x=Rr\sin\theta\sin\phi\\ y=Rr\sin\theta\cos\phi\\ z=Rr\cos\theta\\ w=R\sqrt{1+r^2}$ 并计算其度量 $J^\top GJ=\mathrm{diag}(-1,R^2/(1+r^2),r^2R^2,r^2\sin^2\theta)$ ，对 $\delta(R^2-1)$ 求积分可得度量 $\mathrm ds^2=\frac{1}{1+r^2}\mathrm dr^2+r^2\mathrm d\Omega^2$ 。我们发现它们可以统一到一个框架下： $\mathrm ds^2=\frac{1}{1-Kr^2}\mathrm dr^2+r^2\mathrm d\Omega^2\\$ 其中 $K\in\{-1,0,1\}$ 。这就是宇宙学上FRW度规（Friedmann-Robertson-Walker metric）的一个组成部分，完整的FRW度规需加上时间维 $\mathrm dt$ 以及宇宙标度因子 : $\mathrm ds^2=-c^2\mathrm dt^2+R(t)^2\left(\frac{1}{1-Kr^2}\mathrm dr^2+r^2\mathrm d\Omega^2\right)\\$