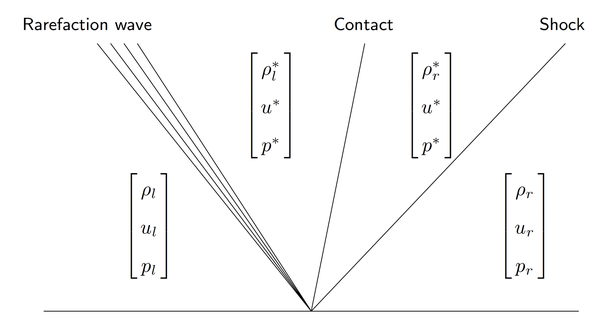
经典网文分享: 计算流体力学——从原理到算法（八）：可压缩无粘流的计算方法（4）Riemann 问题的精确解（初稿）

的确这部分的内容…也就仅仅是理论上严格去算出来，大家可以发现想要理解Riemann问题——流体控制偏微分方程最最基本也非常简单的初值问题，的解，也是异常复杂令人沮丧的一个过程。不仅仅是推理长，复杂繁琐的符号和层出不穷的分类讨论，使得几乎没什么人愿意干嚼完这些知识…所以我暂时也没有太过认真去写这一块，仅仅是强迫自己填了这个部分，以方便我们接着进入实际中最常见的Riemann问题近似解的部分。

我在考虑要不要尝试用视频的形式来展示理论推动过程，不知道有没有那个时间精力。也许也没有人想看吧。

Godunov Scheme的基本思想

在每个单元格点定义体积平均值 $U_i^n$ ，重建分段多项式函数 $\tilde { u } ^ { n } ( x )$ （在 $[x_{i-1/2}, x_{i+1/2}]$ 上定义）（注意，上标n不是指数！代表的是时间为n的时候的分段函数！！）
最简单的情况（分段常数函数）： $\tilde { u } ^ { n } ( x ) = U _ { i } ^ { n } \text{ for } x _ { i - 1/ 2} \leq x < x _ { i -1 / 2}$
使用n-阶分段多项式函数 $\tilde { u } ^ { n } ( x )$ 作为初始条件，在一个时间单位上 $\Delta t$ ，对双曲方程进行精确（或近似）来获得下一步的解 $\tilde { u } ^ { n + 1} ( x )$ 。
在每个单元上求平均值 $U _ { i } ^ { n + 1} = \frac { 1} { \Delta x } \int _ { x _ { i - 1/ 2} } ^ { x _ { i + 1/ 2} } \tilde { u } ^ { n + 1} ( x ) d x$ 以获得新的单元平均值

精确求解一维完全气体的Euler方程的Riemann问题：

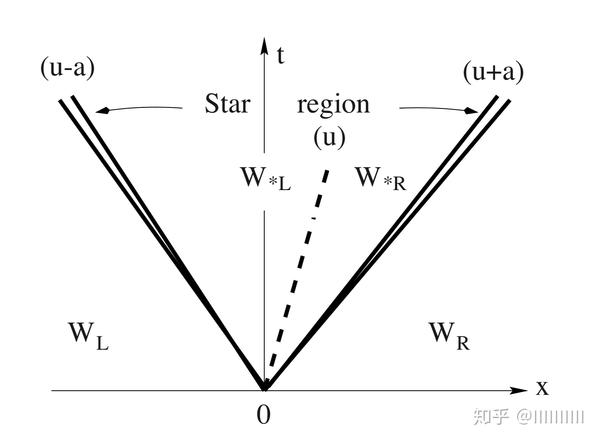
$\mathbf { U } _ { t } + F ( \mathbf { U } ) _ { x } = 0 \\ \mathbf { U } = \left( \begin{array} { c } { \rho } \\ { \rho u} \\ { E } \end{array} \right) = : \left( \begin{array} { c } { u_ { 1} } \\ { u_ { 2} } \\ { u_ { 3} } \end{array} \right) \\ F = \left( \begin{array} { c } { \rho u} \\ { \rho u^ { 2} + p } \\ { u( E + p ) } \end{array} \right) = : \left( \begin{array} { c } { f _ { 1} } \\ { f _ { 2} } \\ { f _ { 3} } \end{array} \right) \\ \mathbf { U }( x ,0) = \mathbf { U }^ { ( 0) } ( x ) = \left\{ \begin{array} { l l } { \mathbf { U }_ { \text{L} } } & { \text{ if } x < 0} \\ { \mathbf { U }_ { R } } & { \text{ if } x > 0} \end{array} \right.$

问题等价于确定 $p _ { * }~~ u _ { * } ~~ \rho _ { * ,L} ~~\rho _ { * ,R}$

对于一般的 $U_{L}， U_R$ ,2-波的类型是接触间断，是已知的，1波和3波，或者是激波，或者是稀疏波——波的类型需要我们计算确认下来。

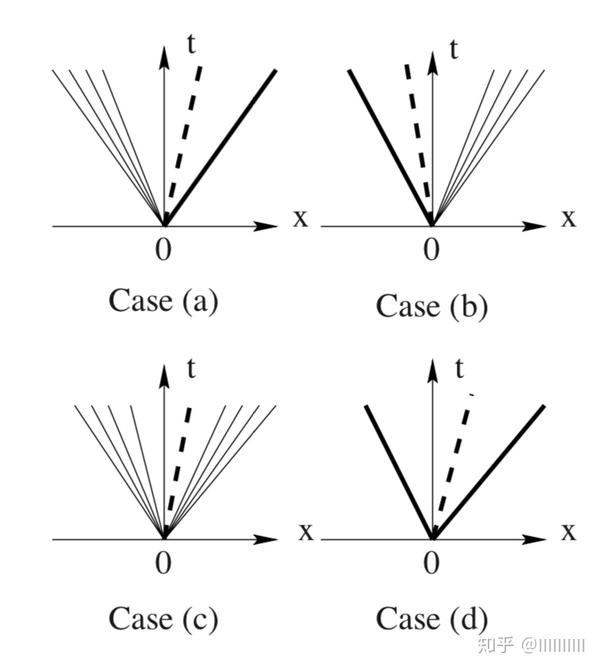
由于压力p穿过2波保持不变，所以寻求关于单个未知压力 $p_{*}$ 的方程就比计算穿过2波有变化的量要容易

$f_L$ 表达式的推导

左波是速度SL的激波：（a）静止参考系，激波速度是SL（b）参考系以速度SL移动，激波速度为零

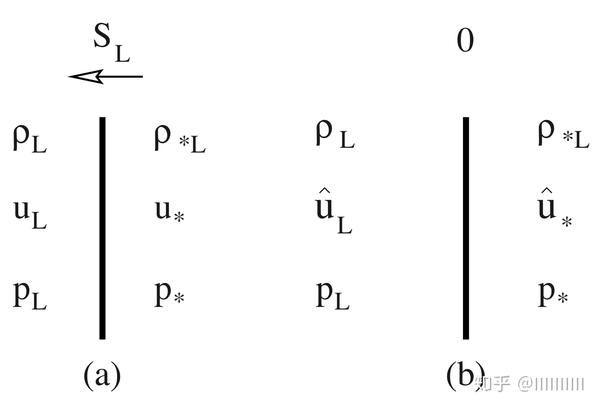
我们假设左激波以 $S_L$ 速度自左向右移动，如图a所示; 波前值为ρL，uL和pL，波后值为ρ* L，u *和p *。

我们选取随激波而一起移动的参照系，如图4.4b所示。在新的框架中，冲击速度为零，相对之下波前波后的速度为: $\hat { u } _ { L } = u _ { L } - S _ { L } ,\hat { u } _ { * } = u _ { * } - S _ { L }$

回顾，第三讲（计算流体力学——从原理到代码（三）：非线性方程的黎曼问题与初等波（超长预警））我们推导出的 Rankine-Hugoniot 条件：

$\left \{\begin{array} { c } \rho _ { L } \hat { u } _ { L } = \rho _ { * L } \hat { u } _ { * } & (1) \\ { \rho _ { \text{L} } \hat { u } _ { \text{L} } ^ { 2} + p _ { \text{L} } = \rho _ { * L } \hat { u } _ { * } ^ { 2} + p _ { * } } &(2) \\ { \hat { u } _ { L } \left( \hat { E } _ { L } + p _ { L } \right) = \hat { u } _ { * } \left( \hat { E } _ { * L } + p _ { * } \right) } &(3)\end{array} \right.$

注意到，单位体积内，密度乘以速度，就是质量从右往左的流量变化，记为 $Q_L$ :

$Q _ { \text{L} } \equiv \rho _ { \text{L} } \hat { u } _ { L } = \rho _ { * L } \hat { u } _ { * }$

第二个公式可以推出：

$\left( \rho _ { \text{L} } \hat { u } _ { \text{L} } \right) \hat { u } _ { L } + p _ { \text{L} } = \left( \rho _ { * L } \hat { u } _ { * } \right) \hat { u } _ { * } + p _ { * } \Rightarrow Q _ { \text{L} } = - \frac { p _ { * } - p _ { \text{L} } } { \hat { u } _ { * } - \hat { u } _ { L } }$

再返回原来的参考系，由参考系的变换关系： $\hat { u } _ { L } = u _ { L } - S _ { L } ,\hat { u } _ { * } = u _ { * } - S _ { L }$ ，QL就得到

$Q _ { \text{L} } = - \frac { p _ { * } - p _ { \text{L} } } { u _ { * } - u _ { \text{L} } }$

所以，未知的 $u_*$ 的表达式：

$u _ { * } = u _ { L } - \frac { \left( p _ { * } - p _ { L } \right) } { Q _ { \text{L} } }$

我们希望，表达式里的自变量，仅仅和已知的物理量 $\mathbf { W } _ { L }$ 以及同样要求的 $p _ { * }$ 有关，于是乎，我们要将 $Q_L$ 进行整理：

$\hat { u } _ { L } = \frac { Q _ { \text{L} } } { \rho _ { \text{L} } } ,\quad \hat { u } _ { * } = \frac { Q _ { L } } { \rho _ { * L } }$ 代入到RH条件得到的第三个公式， $Q _ { \text{L} } ^ { 2} = - \frac { p _ { * } - p _ { \text{L} } } { \frac { 1} { \rho _ { * L } } - \frac { 1} { \rho _ { L } } }$

因为密度 $\rho_{*,L}$ 与 $p_*$ 在左激波处的关系式：

$\rho _ { * \text{L} } = \rho _ { \text{L} } \left[ \frac { \left( \frac { \gamma - 1} { \gamma + 1} \right) + \left( \frac { p _ { * } } { p _ { L } } \right) } { \left( \frac { \gamma - 1} { \gamma + 1} \right) \left( \frac { p _ { * } } { p _ { L } } \right) + 1} \right]$

所以代入QL，得到：

$Q _ { \text{L} } = \left[ \frac { p _ { * } + B _ { \text{L} } } { A _ { \text{L} } } \right] ^ { \frac { 1} { 2} }$

最后带回 $u _ { * } = u _ { L } - \frac { \left( p _ { * } - p _ { L } \right) } { Q _ { \text{L} } }$ , 得到之前我们给出的公式：

$u _ { * } = u _ { L } - f _ { L } \left( p _ { * } ,\mathbf { W } _ { \text{L} } \right)\\ \text{where}~~f _ { L } \left( p _ { * } ,\mathbf { W } _ { L } \right) = \left( p _ { * } - p _ { \text{L} } \right) \left[ \frac { A _ { \text{L} } } { p _ { * } + B _ { \text{L} } } \right] ^ { \frac { 1} { 2} }\\ \text{and}~~ A _ { L } = \frac { 2} { ( \gamma + 1) \rho _ { \text{L} } } ,\quad B _ { \text{L} } = \frac { ( \gamma - 1) } { ( \gamma + 1) } p _ { L }$

左稀疏波：

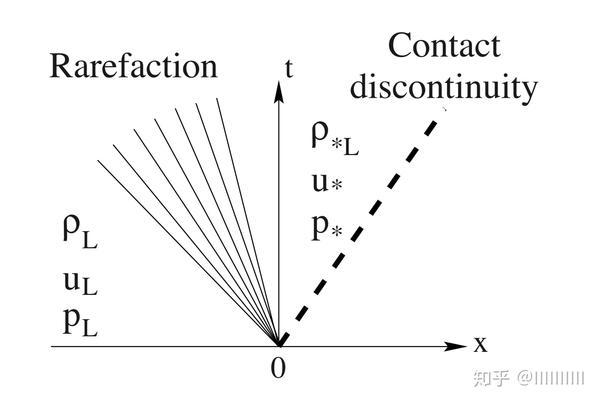
现在我们来推导fL的表达式，其中左波是稀疏波。

未知物理状态 $W_{*L}$ 通过熵条件，连接到左侧已知的初始物理量 $W_L$ ，广义黎曼不变量穿过稀疏波不变。

对于根据热力学等熵定理： $p = C \rho ^ { \gamma }$ ,其中C是一个常数，可以用于各种稀疏波情形。

运用等熵定理，由已知的值计算C的值，即： $C = p _ { \text{L} } / \rho _ { \text{L} } ^ { \gamma }$

因此对于星号区域里面的密度： $\rho _ { * L } = \rho _ { \text{L} } \left( \frac { p _ { * } } { p _ { L } } \right) ^ { \frac { 1} { \gamma } }$

因为广义黎曼不变量 $I_L(u,a)$ 穿过稀疏波是不变的，于是从已知的物理量可以推出： $u _ { L } + \frac { 2a _ { L } } { \gamma - 1} = u _ { * } + \frac { 2a _ { * } L } { \gamma - 1}$

其中 $a_L, a_{*L}$ 即稀疏波的左右状态的声波波速， $a _ { * L } = a _ { L } \left( \frac { p _ { * } } { p _ { L } } \right) ^ { \frac { \gamma - 1} { 2\gamma } }$

带回上面式子 $u _ { L } + \frac { 2a _ { L } } { \gamma - 1} = u _ { * } + \frac { 2a _ { * } L } { \gamma - 1}$ ：

$u _ { * } = u _ { L } - f _ { L } \left( p _ { * } ,\mathbf { W } _ { L } \right)\\ \text{where } f _ { L } \left( p _ { * } ,\text{W} _ { \text{L} } \right) = \frac { 2a _ { \text{L} } } { ( \gamma - 1) } \left[ \left( \frac { p _ { * } } { p _ { L } } \right) ^ { \frac { \gamma - 1} { 2\gamma } } - 1\right]$

$p_∗ , u_∗$ 的解：

$f \left( p ,\mathbf { W } _ { L } ,\mathbf { W } _ { R } \right) \equiv f _ { L } \left( p ,\mathbf { W } _ { L } \right) + f _ { \text{R} } \left( p ,\mathbf { W } _ { R } \right) + \Delta u = 0,\Delta u \equiv u _ { \text{R} } - u _ { \text{L} }$

其中， $f_L$ 具体表达式：

同样的， $f_R$ 的表达式：

$f _ { \text{R} } \left( p ,\mathbf { W } _ { R } \right) = \left\{ \begin{array} { l } { \left( p - p _ { R } \right) \left[ \frac { A _ { R } } { p + B _ { R } } \right] ^ { \frac { 1} { 2} } } &{\text{if}~~ p >p_R} \\ { \frac { 2a _ { R } } { ( \gamma - 1) } \left[ \left( \frac { p } { p _ { R } } \right) ^ { \frac { \gamma - 1} { 2\gamma } } - 1\right] } &{\text{if}~~ p \le p_R} \end{array}\right.$

而式子中， $A _ { L } ,B _ { L } ,A _ { R } ,B _ { R }$ 由Riemann初值决定：

$A _ { L } = \frac { 2} { ( \gamma + 1) \rho _ { \text{L} } } ,\quad B _ { \text{L} } = \frac { ( \gamma - 1) } { ( \gamma + 1) } p _ { L }\\ A _ { R } = \frac { 2} { ( \gamma + 1) \rho _ { \text{R} } } ,\quad B _ { \text{R} } = \frac { ( \gamma - 1) } { ( \gamma + 1) } p _ { \text{R} }$

中间星号区域的速度 $u_*$ 的公式：

$u _ { * } = \frac { 1} { 2} \left( u _ { L } + u _ { R } \right) + \frac { 1} { 2} \left[ f _ { R } \left( p _ { * } \right) - f _ { L } \left( p _ { * } \right) \right]$

给定了Riemann问题的初值： $\rho _ { L } ,u _ { L } ,p _ { L } \text{ and } \rho _ { R } ,u _ { R } ,p _ { R }$ ，我们前面推导出了关于中间区域压力的方程：

$f _ { L } \left( p ,\mathbf { W } _ { L } \right) = \left\{ \begin{array} { l} { \left( p - p _ { L } \right) \left[ \frac { A _ { L } } { p + B _ { L } } \right] ^ { \frac { 1} { 2} } } & { \text{ if } p > p _ { L } } \\ { \frac { 2a _ { L } } { ( \gamma - 1) } \left[ \left( \frac { p } { p _ { L } } \right) ^ { \frac { \gamma - 1} { 2\gamma } } - 1\right]}&{ \text{ if } p \leq p _ { L } } \end{array} \right.\\ f _ { \text{R} } \left( p ,\mathbf { W } _ { R } \right) = \left\{ \begin{array} { l } { \left( p - p _ { R } \right) \left[ \frac { A _ { R } } { p + B _ { R } } \right] ^ { \frac { 1} { 2} } } &{\text{if}~~ p >p_R} \\ { \frac { 2a _ { R } } { ( \gamma - 1) } \left[ \left( \frac { p } { p _ { R } } \right) ^ { \frac { \gamma - 1} { 2\gamma } } - 1\right] } &{\text{if}~~ p \le p_R} \end{array}\right.$

我们下面研究这个函数的性质（因为我们想着，如果函数性质不好，再好的解析表达式，也很难求解，最简单就比如说高次多项式求根）

那么

$f'_K = \frac{\partial f_K(p,\textbf{W}_K)}{\partial p}, ( K = L ,R )\\ \Rightarrow f _ { K } ^ { \prime } = \left\{ \begin{array} { l} { \left( \frac { A _ { K } } { B _ { K + p } } \right) ^ { 1/ 2} \left[ 1- \frac { p - p _ { K } } { 2\left( B _ { K } + p \right) } \right] } &{\text{ if } p > p _ { K } \text{ (shock) }} \\ { \frac { 1} { \rho _ { K } a _ { K } } \left( \frac { p } { p _ { K } } \right) ^ { - ( \gamma + 1) / 2\gamma } } & \text{ if } p \leq p _ { K } ( \text{ rarefaction } ) \end{array} \right.$

因为 $f '= f'_L + f'_R$ ，由于 $f'_K > 0$ ，所以 $f(p)$ 是单调函数

接着，我们来看二次导数

$f''_K= \left\{ \begin{array} { l } { - \frac { 1} { 4} \left( \frac { A _ { K } } { B _ { K } + p } \right) ^ { 1/ 2} \left[ \frac { 4B _ { K } + 3p + p _ { K } } { \left( B _ { K } + p \right) ^ { 2} } \right] } &\text{ if } p > p _ { K } ( \text{ shock } ) \\ { - \frac { ( \gamma + 1) a _ { K } } { 2\gamma ^ { 2} p _ { K } ^ { 2} } \left( \frac { p } { p _ { K } } \right) ^ { - ( 3\gamma + 1) / 2\gamma } } & \text{ if } p \leq p _ { K } ( \text{ rarefaction } ) \end{array} \right.$

因为 $f''_K < 0 \Rightarrow f ^ { \prime \prime } = f _ { L } ^ { \prime \prime } + f _ { R } ^ { \prime \prime } < 0$ ，所以 $f(p)$ 增长率越来越小，直观来看：

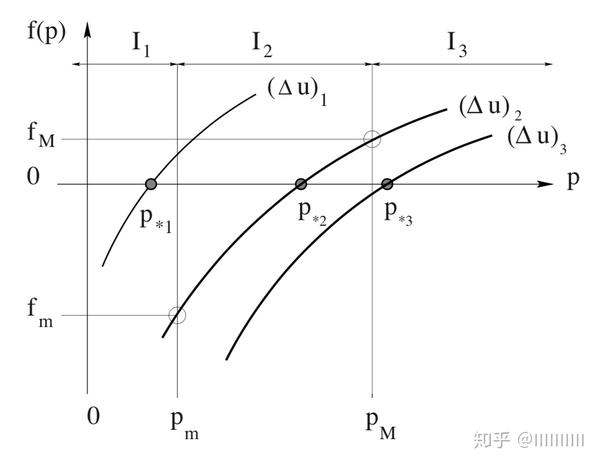
f(p) 的这种性质，决定了我们可以选取适当的迭代法，来寻找 $f(p)= 0$ 的零点 $p_*$ ，而两个重要的参数分别是：速度差 $Δu= uR-uL$ 和压力值 $p_L, p_R$ 。

因此，定义：

$p _ { \min } = \min \left( p _ { L } ,p _ { \text{R} } \right) ,\quad p _ { \text{max} } = \max \left( p _ { L } ,p _ { \text{R} } \right)\\ f _ { \min } = f \left( p _ { \min } \right) ,\quad f _ { \max } = f \left( p _ { \max } \right)$

对于给定的压力值 $p_L, p_R$ ，实际上是速度差 $Δu= uR-uL$ 决定了 $p_*$ 的值，那么我们考虑三个区间：

$p _ { * } \operatorname{lies} \text{ in } I _ { 1} = \left( 0,p _ { \min } \right) \quad \text{ if } f _ { \text{min} } > 0\text{ and } f _ { \max } > 0\\ p _ { * } \operatorname{lies} \text{ in } I _ { 2} = \left[ p _ { \min } ,p _ { \max } \right] \text{ if } f _ { \min } \leq 0\text{ and } f _ { \max } \geq 0 \\ p _ { * } \operatorname{lies} \text{ in } I _ { 3} = \left( p _ { \text{max} } ,\infty \right) \quad \text{ if } f _ { \text{min} } < 0\text{ and } f _ { \text{max} } < 0$

对足够大的 $\Delta u$ ，比如说上图中的 $(\Delta u)_1$ ，解 $p _* = p _{* 1}$ ，位于 I1 区间里面，因此 $p _* <p_L，p_ * <p_R$ ， 所以两个非线性波都是稀疏波。

如果的 $Δu = (Δu)2$ ， $p_ * = p _{* 2}$ 位于pL和pR之间，因此一个非线性波是一个稀疏波，另一个是冲击波。

对于足够小的Δu值，如图中的 $(Δu)3$ ， $p_ * = p _{* 3}$ 位于I3中，即 $p _*> p_L，p_ *> p_R$ ，这意味着两个非线性波都是冲击波。

总之，我们通过 fmin 和 fmax 的符号来识别p *所在的区间。

关于 f(p) 的另一个观察是：在 I1 中，f'(p) 和 f''(p) 快速变化; 当搜索 f(p)= 0 的根时，可能产生数值上的困难。——相比而言，随着p增大，f(p) 的形状趋于类似于直线的形状，求根会轻松很多。

关于真空：

此外，对于非真空初始数据W_L，W_R，如果Δu足够小，则存在用于压力的唯一正解p *。事实上，即使对于数据状态为非真空状态的情况，在黎曼问题的解中，Δu 大于临界值（Δu）的值也会导致真空。

临界值可以根据初始物理量进行分析。很显然，对于压力p *的正解，我们需要f（0）<0，即正压力条件

$( \Delta u ) _ { \text{ crit } } \equiv \frac { 2a _ { L } } { \gamma - 1} + \frac { 2a _ { R } } { \gamma - 1} > u _ { R } - u _ { L }$

如果违反这种条件，则非线性波会产生真空。在这种情况下，解决方案的结构与图4.1中描述的不同，解决方法也是如此，我们将在后面有机会讨论

function [ f ] = f_star( p_star,p,rho )  % f_star function of Godunov Scheme  %   p_star: static pressure after the wave  %   p: static pressure before the wave  %   rho: density before the wave  %   f: value of f(p_star)    global gamma R;    T = p/R/rho;% ideal gas  c = sqrt(gamma*R*T);    if p_star>p      f = (p_star-p)/rho/c/sqrt((gamma+1)/2/gamma*p_star/p+(gamma-1)/2/gamma);  else      f = 2*c/(gamma-1)*((p_star/p).^((gamma-1)/2/gamma)-1);  end  end

function F = godunov_scheme(U_l,U_r,t)  % Computing F_i+1/2 Using Godunov Scheme  %   U_l: [rho rho*u rho*E] on the left side  %   U_r: [rho rho*u rho*E] on the right side  %   t: time  %   F: [rho*u u^2+p rho*u*H]     global gamma R;    W_l     = Q2S(U_l);  W_r     = Q2S(U_r);    rho_1   = W_l(:,1);  u_1     = W_l(:,2);  p_1     = W_l(:,3);  rho_2   = W_r(:,1);  u_2     = W_r(:,2);  p_2     = W_r(:,3);    F_0     = f_star(0,p_1,rho_1)+f_star(0,p_2,rho_2);  F_p1    = f_star(p_1,p_1,rho_1)+f_star(p_1,p_2,rho_2);  F_p2    = f_star(p_2,p_1,rho_1)+f_star(p_2,p_2,rho_2);  du      = u_1-u_2;    % determine which condition the problem belongs to  if du<=F_0      condition=5;  elseif du>F_0 && du<=min(F_p1,F_p2)      condition=4;  elseif du>max(F_p1,F_p2)      condition=1;  else      if p_1>p_2          condition=2;      else          condition=3;      end  end    %solving equation using Newton Method  fun = @(p_star)f_star(p_star,p_1,rho_1)+f_star(p_star,p_2,rho_2)-du;  [p_star,fval] = fsolve(fun,0.5*(p_1+p_2),optimset('Display','off','TolFun',1e-10));  u_star = 0.5*(u_1+u_2+f_star(p_star,p_2,rho_2)-f_star(p_star,p_1,rho_1));  % fprintf('fval = %.4e\n',fval);    % constant parameters  T_1    = p_1/R/rho_1;% ideal gas  c_1    = sqrt(gamma*R*T_1);  A_1    = rho_1*c_1*sqrt((gamma+1)/2/gamma*p_star/p_1+(gamma-1)/2/gamma);  T_2    = p_2/R/rho_2;% ideal gas  c_2    = sqrt(gamma*R*T_2);  A_2    = rho_2*c_2*sqrt((gamma+1)/2/gamma*p_star/p_2+(gamma-1)/2/gamma);      switch condition % computing left wave      case {1,3}          rho_1_star  = rho_1*A_1/(A_1-rho_1*(u_1-u_star));          z_1h        = u_1-A_1/rho_1;          z_1t        = z_1h;      case {2,4}          c_1_star    = c_1+(gamma-1)*(u_1-u_star)/2;          rho_1_star  = gamma*p_star/c_1_star^2;          z_1h        = u_1-c_1;          z_1t        = u_star-c_1_star;      case {5}          c_1_star    = c_1+(gamma-1)*(u_1-u_star)/2;          rho_1_star  = gamma*p_star/c_1_star^2;          z_1h        = u_1-c_1;          z_1t        = u_1-2/(gamma-1)/c_1;  end    switch condition % computing right wave      case {1,2}          rho_2_star  =  rho_2*A_2/(A_2-rho_2*(u_star-u_2));          z_2h        = u_2+A_2/rho_2;          z_2t        = z_2h;      case {3,4}          c_2_star    = c_2+(gamma-1)*(u_star-u_2)/2;          rho_2_star  = gamma*p_star/c_2_star^2;          z_2h        = u_2+c_2;          z_2t        = u_star+c_2_star;      case{5}          c_2_star    = c_2+(gamma-1)*(u_star-u_2)/2;          rho_2_star  = gamma*p_star/c_2_star^2;          z_2h        = u_2+c_2;          z_2t        = u_2+2/(gamma-1)/c_2;  end    x = 0;    if x<z_1h*t      u        = u_1;      p        = p_1;      rho      = rho_1;  elseif x>= z_1h*t && x<z_1t*t      c_i      = (gamma-1)/(gamma+1)*(u_1-x/t)+2/(gamma+1)*c_1;      u        = x/t+c_i;      p        = p_1*(c_i/c_1)^(2*gamma/(gamma-1));      rho      = gamma*p/c_i^2;  elseif x>= z_1t*t && x<z_2t*t      u        = u_star;      p        = p_star;      if x<u_star*t          rho  = rho_1_star;      else          rho  = rho_2_star;      end  elseif x>= z_2t*t && x<z_2h*t      c_i      = (gamma-1)/(gamma+1)*(x/t-u_2)+2/(gamma+1)*c_2;      u        = x/t-c_i;      p        = p_2*(c_i/c_2)^(2*gamma/(gamma-1));      rho      = gamma*p/c_i^2;  elseif x>= z_2h*t      u        = u_2;      p        = p_2;      rho      = rho_2;  end    F = W2F([ rho,u,p ]);  end

来源：知乎 www.zhihu.com
作者：知乎用户（登录查看详情）

【知乎日报】千万用户的选择，做朋友圈里的新鲜事分享大牛。点击下载

经典网文分享

计算流体力学——从原理到算法（八）：可压缩无粘流的计算方法（4）Riemann 问题的精确解（初稿）

没有评论:

发表评论