
这是一篇科普大统一理论和模型相关问题的文章。这方面的问题可以讲很多,而且讲得很深。这里我只挑其中的一部分来讲,而且讲得非常浅。为了能突出不同的点,文章会采用问答的形式,并且按照从易到难的顺序排列。在解释某些问题的时候,我可能并不会按照历史发展的顺序来讲(因为我也不清楚历史的顺序),而是按照(我认为)能最好地解释问题的思路来讲。
这次也加了很多括号,括号中的部分涉及到一些量子场论的知识;不看也不影响阅读。
一些常见的科普层次的问题:
这个理论的名字是"大统一"还是"大一统"?
我们正在讨论的这个理论叫做"大统一"而不是"大一统"。"大一统"指的是一个国家在政治权力、税收等经济制度和思想文化上的高度集中。比如,汉武帝时期,中央集权,独尊儒术,这是"大一统"。"大统一"只是英文grand unified theories的翻译。非专业人士可能会把这两个相似的名词搞混,但是把人家的名字搞错很不礼貌。
"大统一"想要统一什么?
这个理论想要统一的是电磁相互作用、弱相互作用和强相互作用这三种(Yang-Mills类型的规范)相互作用。一般的大统一理论和唯象都不涉及到统一引力的问题。大统一理论也不讨论引力的量子化问题。
这个理论也不是想把上面提到的三种相互作用都量子化。这三种相互作用的量子化早就已经解决了。物理学家们想做的事情是把这三种(规范)相互作用写成同一种(规范)相互作用。
"大统一"如果实现,对我们的生活/现在的物理理论有什么影响吗?
除了上报纸、称为科幻爱好者的谈资之外,对我们的生活几乎没有任何影响。之前的文章(这个专栏下的第一篇文章)中也介绍了,现代物理学的一个信念是"physics laws at different scales never talk to each other"(在不同尺度上有不同的物理规律)。并且,现在的大统一模型在低能情况下肯定是要变成粒子物理的标准模型的。如果粒子物理的标准模型对于解释人们能日常接触到的问题没有任何帮助(事实上它们确实没有),那么大统一模型也不会有任何帮助。
对于物理理论,个人感觉,大统一理论更像是在规范场论和超对称理论的框架下搭建粒子物理的新模型。它更侧重于唯象而不是研究场论本身的问题,所以对物理理论的发展的影响也不大。(当然,出现这种印象也可能是因为我之前做的是大统一的唯象学。)
一些硬一些的问题:
标准模型中的规范相互作用不是已经统一成 了吗?
这并不是我们想要的"统一"。我们想要的是把规范群 看成是一种规范相互作用(即,一个半单李群作为规范群的相互作用)在破缺后剩余的部分。这看起来是一个很任性的要求,但是我们在下一个问题中会给出支持这个观点的证据。
大统一理论的动机是什么?
(圈图水平的)量子修正会让相互作用的耦合常数——电磁相互作用中的电荷e、弱相互作用中的弱荷和强相互作用中的色荷不再是常数,而是随着粒子(质心系中)的能量(能标)的变化而改变。量子场论可以计算这些耦合常数的变化。
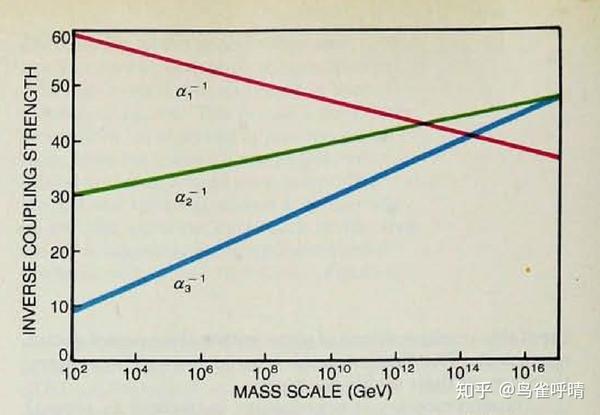
我们发现,标准模型中的三种耦合常数——电荷(图中的红线)、弱荷和色荷(图中的绿线和蓝线)对应的线在能量很高时会相交。不过这三条线并不是严格的交于一点。然而,在加上超对称之后,我们发现,这三条线几乎真的交在同一个点上。这表明在一个能标上,这三种相互作用的耦合常数相等,从而它们有可能被看成是同一个(规范)相互作用。
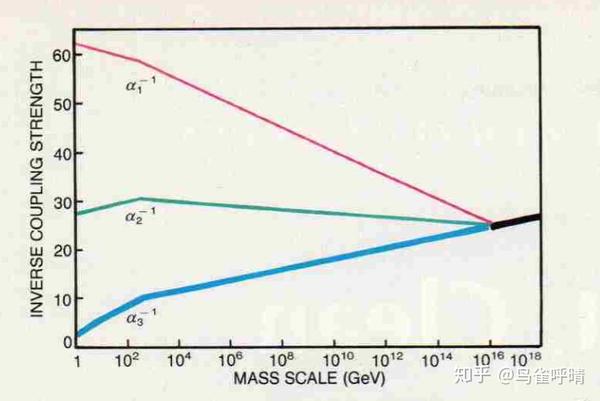
超对称在过去很长的一段时间内曾被认为是解决标粒子物理准模型中的large hierarchy问题的标准答案(这个问题又是另一个故事了,这里不展开讲),观测到超对称是迟早的事情。(现在看来似乎被打脸了。)所以如果加上超对称之后的标准模型中,三种相互作用的耦合常数能在某个能标上相等,那么它们的"统一"看起来也非常有前景。(这也是大部分的大统一模型都会加上超对称的原因。)
(这两张图片来自Savas Dimopoulos, Stuart Raby, Frank Wilczek三个人的文章。这篇文章首次计算了在有超对称的情况下耦合常数的跑动。搜这三个人的名字,就可以看到那篇古老的文章。)
另一方面,宇宙学的观测暗示,我们需要能破坏重子数的相互作用,而大统一理论中自然地会带有重子和轻子相互转变的项。目前的宇宙学观测表明,正物质要比反物质多,但是粒子物理中,正反物质在相互作用中是"对称"的。(比如,初末动量分别相同时,电子对到电子对的散射截面和正电子对到正电子对的散射截面是一样的。)自然界没理由偏袒正反物质中的一种,所以早期的宇宙中正反物质应该是等量的。但是,这样就会导致,宇宙降温后,正反物质相互湮灭,几乎剩不下重子物质。为了得到我们现在观测到的宇宙,需要正物质中的重子物质要比反物质中的重子物质多一点点(定义一个量 ,其中
是单位体积内的重子数密度,
是单位体积内的反重子数密度。根据现在的观测,可以推出
,即,在1亿个正重子所占的体积内,正重子只需要比反重子多3个。)。如果它们一开始是等量的,那怎么演变成一个比另一个多呢?这就需要存在轻子和重子相互转化的过程。某种涨落导致正物质这边有一部分轻子转化成重子即可。而大统一理论中恰好带有这种相互作用。(当然,也有不用大统一理论也能让重子和轻子相互转化的模型。但是目前实验上没观测到重子和轻子的相互转化,强行在拉氏量总加上这么一个相互作用感觉不太自然。如果有大统一的话,这一项就会变得自然很多。)
大统一理论有可观测的效应吗?
有的。几乎所有大统一理论的模型都会预言质子会衰变,但是不同的模型给出的寿命不一样。从 年到
年不等。2015年,日本的超级神冈探测器给出了质子的寿命的下限约为
年。
(质子的寿命如此长,我们如何观测质子的衰变?其实粒子的"寿命"是一个统计概念,它反映的是粒子衰变的概率。粒子衰变的概率越小,它的寿命就越长。我们可以囤积大量的某种粒子,然后观测这一堆粒子中是否有粒子衰变,从而定出粒子的衰变概率或者至少定出衰变概率的上限,从而推测出粒子的寿命。)
大统一理论还预言了一些耦合常数之间的关系。在Polchinski的string theory第一册第一章第一节中,他提到了"It (指大统一理论) also successfully predicts one of the three parameters (the weak mixing angle) and possibly another (the bottom-tau ratio)."不确定现在的测量结果是不是还符合预言。
大统一理论中,还有重子和轻子的相互转化。不过我们目前没有观测到这种反应。
"大统一"要如何统一各种相互作用?
这个问题可以换一个问法: 能作为哪些群的子群?只要我们找到了这些群,那么我们就可以通过适当的机制将这个更大的群破缺/约化成
这个子群。
有许多种办法来寻找这些可能的群。这里我们主要介绍规范群是 的模型。选择这个模型的原因也会在下面提到。
一些办法会先介绍Pati-Salam模型(规范群是 ,其中四种color中前三种就是QCD的色,第四种color是轻子数)和SU(5)模型,然后说它们都是
的子群(
是最小的能同时包含这两个群作为子群的群),从而确定规范群是
.
当然,有更聪明的办法来确定这个群是 :
如果规范相互作用都被统一了,那么每代费米子中的部分或者全部将被看成是一个表示的不同分量。最好的大统一的结果应该是每代费米子(两个夸克、两个轻子)的所有自由度(这里,自由度指的是外尔费米子,或者说是不可约旋量表示中的旋量。夸克和轻子分别有左手和右手两个自由度,每个夸克还有三种颜色,一共是 个自由度)统一成一个旋量表示。每个外尔费米子是一个2分量旋量,所以16个自由度/16个2分量旋量形成一个32分量的旋量,其左、右手部分各有16个分量。熟悉群表示的同学应该知道,这正是
的旋量表示的特点。所以每代的费米子形成一个
的旋量表示,那么对应的规范群就应该是
。(这也是我选取这个模型来讲的原因。)
大统一没有统一什么?
除规范相互作用外其他的相互作用——Higgs和其他场的Yukawa相互作用。(不过与标准模型不同,大统一理论中,每一代的费米子都被统一在一起变成 的不可约旋量表示
,Higgs和
耦合而不是和每种费米子单独耦合。这减少了一些参数。超对称也给
的超对称伴子和Higgs场的耦合加上了限制。)
"大统一"的模型有什么缺点?
标准模型的一个问题就是参数太多,大统一理论的模型中的参数也不少。大统一看上去减少了很多参数,但是为了让搭建的模型的预言和实验结果能对上,我们需要手动加入破坏超对称的项。除此之外,我们还需要限制Yukawa相互作用中能取的项,这需要我们引入Froggatt-Nielson states和一些新的离散的 global对称性。这些东西引入了新的参数,使得大统一的参数并没有比标准模型的参数明显减少,甚至可能还更多。(1505.00264这篇文章中用到的模型就一共有24个自由参数。)
而且模型里引入了越来越多的对称性,但是依然没能直接回答,为什么要有这些对称性。看起来唯一的理由就是"这样构造的模型的预言和实验数据能对上"。这让人很烦躁。
大统一的能标是 GeV,而Higgs的真空稳定性在
GeV左右出现问题。也许在
GeV之前就会出现新物理,从而让现有的大统一模型失去基础。即使不考虑Higgs的真空稳定性问题,我们也不知道,在大统一能标和目前的实验能标这巨大的能量差之间是不是还有新物理。
当然,对于使用超对称的大统一模型,最大的问题就是实验上还没看到超对称。相应地,这些模型需要调整自身的参数,让使用的超对称粒子的质量超过实验给出的超对称粒子质量下限。但是,这种参数调整可能会让其他可观测量的拟合变差。差到一定程度,一个模型就被排除了。随着实验数据精度的提高,一部分模型已经被排除,而没被排除的模型的参数空间也被压缩了很大一部分,几乎只能"苟活"。
现在还可以从事大统一的理论或者唯象方面的研究吗?
如果你想在学术圈生存下去的话,不建议再去做这方面的研究。唯象的话,实验上长期没有发现相应的粒子,导致人们已经逐渐不再关注这个领域。发这方面的文章很难获得引用。理论的话,个人感觉这个理论中除了用到了超对称,几乎没有超出规范场论课程的新的东西。
更新预告:下次就是讲单粒子的单圈和闭弦的单圈了!
来源:知乎 www.zhihu.com
作者:鸟雀呼晴
【知乎日报】千万用户的选择,做朋友圈里的新鲜事分享大牛。 点击下载
没有评论:
发表评论