21世纪前，数学界最著名的猜想之一就是四色猜想了。可能很多人都听说过：对任意的（平面上的）地图染色，要求相邻的国家颜色不同，只需要四种颜色就足够了。
这个猜想正式提出是在1852年，其实在之前已经广为流传了。很多数学家尝试从各种角度去接近这个猜想，也提出了各种错误的证明。最终在一个多世纪之后，Appel和Haken在计算机的帮助下证明了这个猜想。不过因为证明主要依靠计算机，至今人们也不是特别清楚，为什么四种颜色就足够了。
我们可以把四色猜想，或者说四色定理，从"地图"等价的转换到"图"上。图，不严谨的说就是点和边连成的图形。在图论中有一个定义叫平面图，说的是一种图可以在平面上画出，并且边之间两两不相交。我们把地图上的每个国家看成一个点，两个国家相邻就代表这两个点之间存在一条边。这样，我们就得到了一个平面图，对国家染色也就变成了对图中的点染色，使得相邻的点不同色。四色定理说，对于任意平面图，四种颜色就足够满足上面的条件了。
很多对四色定理的错误证明源于下面的一个错误观察：很多人觉得，如果对图的点染色，需要四种颜色，一定是因为图的某个区域包含了四个两两相邻的点；同理，如果需要五种颜色，也一定是因为图的某个区域包含了五个两两相邻的点。接下来只要证明，大于等于五个点两两相连的图不能在平面上画出，就证完了。
首先，大于等于五个点两两相连的图，确实是不能在平面画出的。（在图论中， 
那么一个图如果不包含五阶完全图，一定可以用四种颜色染色吗？我们考虑弱化的情形，但是原理相同：如果一个图不包含三阶完全图，即三角形，一定两种颜色就够了吗？下面是一个很容易的反例。
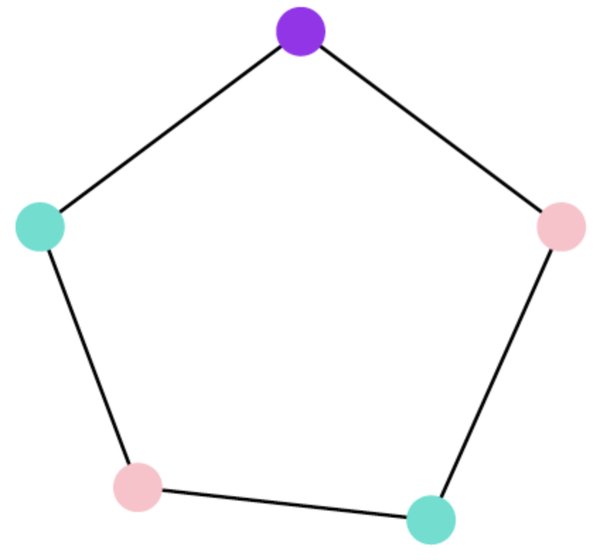
这告诉我们，试图从图中包含的完全子图的大小来讨论，是错误的方向。实际上Erdos构造了不包含三角形（当然也不包含其他大于三阶的完全图），但是需要染色数任意大的图。
那么，到底是什么力量，在驱使着一个图，需要很多个颜色来染色呢？
这个看起来很自然的问题，人们还不知道。因此图的染色数问题，一直是数学界研究的重点之一。但是人们对此有一些看起来很正确，只等待证明的猜想：比如Hadwiger猜想。这个猜想也是组合数学最深刻的猜想之一，应该也是最没有希望短期内被证明的猜想之一了。在介绍这个猜想之前，我先简单介绍一下Robertson和Seymour引入的一个重要概念：Graph Minor。
其实很类似于矩阵的Minor。一个小的图 
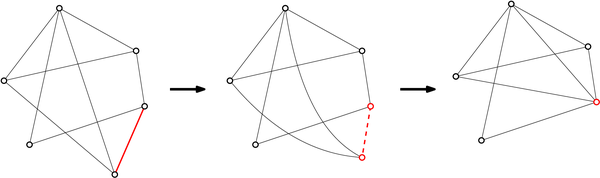
现在，graph minor本身已经成为图论的一个研究重点了，数学家们也相信graph minor是一个正确的研究对象。原因主要是由于Kuratowski定理。Kuratowski定理给了我们平面图的结构，一个图 
Kuratowski's Theorem
图
Robertson和Seymour成功的将其推广到了任意图：图 
最后回到图的染色问题。刚才我们提到，很多人错误的认为，一个图不包含 
Hadwiger's Conjecture
如果图
只要把"子图"换成"minor"，一个错误的观察就变成了深刻的猜想。由于人们认为graph minor是正确的语言，因此很多人认为Hadwiger猜想是正确的。不过猜想的进展非常缓慢：
如果Hadwiger猜想成立，说明人们已经大致理解任意图的大体结构了。回到最开始提到的五边形的反例：之所以五边形虽然没有三角形，但是需要三种颜色，很可能由于它包含了三角形做为Minor。
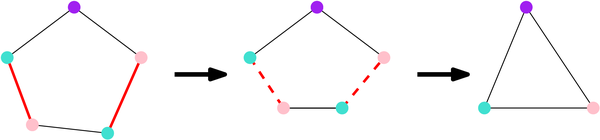
图的染色数一直是一个数学家很想理解又很难理解的东西，四色猜想给了大家一个从图的结构或者拓扑性质入手的契机。数学家想证明黎曼猜想是因为黎曼猜想的推论真的很有用，而数学家想证明四色猜想并不是真的要用四种颜色染地图，而是想搞清楚染色数和图结构的关系。然而Appel和Haken用计算机的证明，并不能告诉我们想要的结果，这也是大家对这个证明有些失望的原因。至今，四色定理没有不依赖计算机的证明。因此图的染色数和结构的关系，伴随Hadwiger猜想，还不是人们目前的智力和技术能探及的区域。
来源：知乎 www.zhihu.com
作者：Yifan
【知乎日报】千万用户的选择，做朋友圈里的新鲜事分享大牛。 点击下载
没有评论:
发表评论