经典网文分享: 11220 一道弹性碰撞的物理题，结果为什么会出现 π ？

　　YouTube 上的 3blue1brown 频道昨天发布了一个视频，介绍了一道有趣的物理题：

如题图所示，光滑的地面上放着大小两个滑块，左边是墙。大滑块的质量是小滑块的 $n$ 倍。给大滑块一个向左的初速度，两个滑块之间，以及小滑块与墙之间会发生多次碰撞。假设碰撞没有能量损失，问一共会发生多少次碰撞？

　　你可能觉得，这只是一道普通的物理题而已，没什么意思。先别走，我们来看看 $n$ 取一些特殊值时，一共会发生的碰撞次数：

若两个滑块质量相等，则一共会发生 3 次碰撞；
若大滑块的质量是小滑块的 100 倍，则一共会发生 31 次碰撞；
若大滑块的质量是小滑块的 1 万倍，则一共会发生 314 次碰撞；
若大滑块的质量是小滑块的 1 百万倍，则一共会发生 3,141 次碰撞；
若大滑块的质量是小滑块的 1 亿倍，则一共会发生 31,415 次碰撞……

　　是不是觉得有意思了？当两个滑块质量之比是 100 的幂时，碰撞次数会是 $\pi$ 的前若干位。这么一道「方方正正」的物理题里，怎么会出现与圆有关的 $\pi$ 呢？！

　　3blue1brown 频道在这里卖了个关子，要到一周之后才会发布详解。不过它给了一个提示：凡是出人意料地出现 $\pi$ 的题目，背后总是隐藏着一个圆。而这道物理题里的圆，隐藏在能量守恒方程中（式中 $M,m$ 表示大小滑块的质量， $V,v$ 表示大小滑块的速度）：

$\frac{1}{2}mv^2 + \frac{1}{2}MV^2 = \text{常数} \\$

　　这篇文章就来「剧透」一下， $\pi$ 是怎么出现的。本文的方法不一定与一周后将要发布的解法相同，我也鼓励读者在继续看下去之前，先自己捣鼓捣鼓，看看能不能捣鼓出 $\pi$ 来。

　　能量守恒方程式，实际上表示了 $v-V$ 空间中的一个椭圆。设大滑块的初速度为 $-1$ （负号代表向左），则能量守恒方程式可以化简为：

$\frac{v^2}{n} + V^2 = 1 \\$

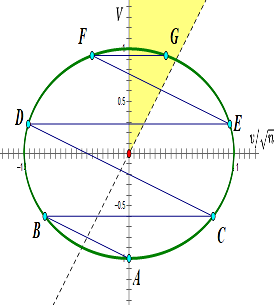
这个方程式表示的椭圆如下图所示（图中取 $n=4$ ）。在运动过程中的任何时刻，两个滑块的速度都会落在椭圆上；两个滑块的初速度，对应着短轴的下端（下图 A 点）。

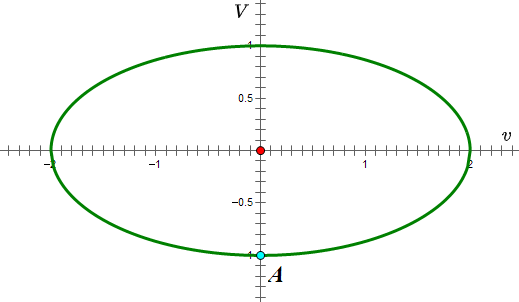
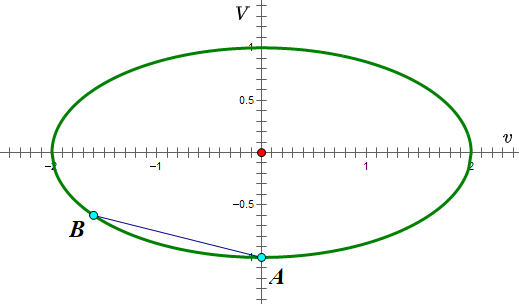
　　下面我们试着在椭圆中画出碰撞过程。第一次碰撞，是大滑块撞小滑块。碰撞前后，两个滑块的速度除了满足能量守恒以外，还要满足动量守恒，即：

$mv + MV = \text{常数} \\$

这在 $v-V$ 空间中，代表了一条斜率为 $-m/M = -1/n$ 的直线。过 A 点做一条斜率为 $-1/n$ 的直线，它与椭圆的交点 B 就代表了第一次碰撞后，两个滑块的速度。

　　第二次碰撞，是小滑块撞墙。其结果很简单，就是小滑块的速度反向。在图上，过 B 点画一条与横轴平行的直线，它与椭圆的交点 C 就代表了碰撞后两个滑块的速度。

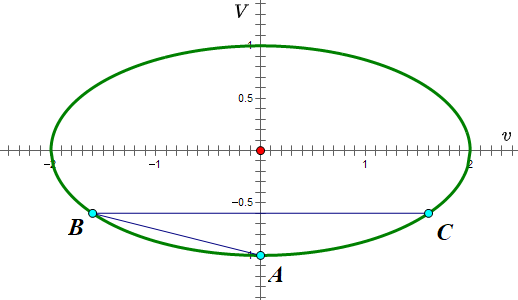
　　上述过程可以重复下去，直到 $V \ge v \ge 0$ 时为止。此时，两个滑块都向右运动，但小滑块追不上大滑块了，于是不会再发生碰撞。在 $v-V$ 空间中，代表两个滑块最终速度的点（下图中为 G），一定会位于第一象限中上面这一半（图中的黄色区域）。

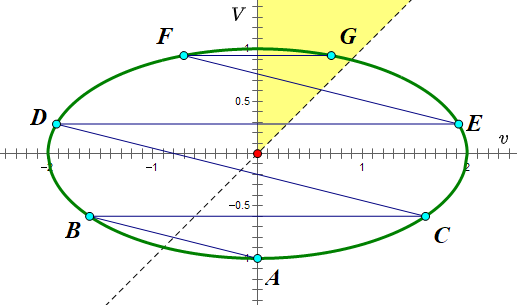
　　在上图中可以注意到，弧 AC、BD、CE、DF、EG 所对的「椭圆周角」（角 B、C、D、E、F）都是相等的，等于 $\arctan(1/n)$ 。弧 AB 与 AC 对称，也可以让它对应「椭圆周角」ACB，这个角也等于 $\arctan(1/n)$ 。联想到圆中有「等弧所对圆周角相等」，而椭圆中则没有这个性质，于是想到：把椭圆给「捏」成圆，怎么样？

　　将上图整体在横向上压缩到原来的 $1/\sqrt{n}$ 倍，则椭圆就变成了单位圆：

这样一压缩，线段 AB、CD、EF 的斜率就都从 $-1/n$ 变成了 $-1/\sqrt{n}$ ，各段圆弧（除了 FG）所对的圆周角也都变成了 $\arctan(1/\sqrt{n})$ 。现在可以利用「等弧所对圆周角相等」了 —— 这些圆弧的长度，就都等于这个圆周角的 2 倍，即 $2\arctan(1/\sqrt{n})$ 。

　　滑块的每一次碰撞，都可以看成是从单位圆上切下一段长度为 $2\arctan(1/\sqrt{n})$ 的圆弧，直到剩余部分长度不超过 $2\arctan(1/\sqrt{n})$ 为止。而整个单位圆的周长是 $2\pi$ （注意 $\pi$ 出现了！），于是就可以得到总的碰撞次数：

$\left\lceil \frac{2\pi}{2\arctan(1/\sqrt{n})} \right\rceil-1 \\$

这里的取整号看起来较复杂，实际想要达到的效果是，一般情况（不能整除时）取下整，特殊情况（能整除时）取商再减一。请读者自行验证。

　　由上式可以算出，当两个滑块质量相等时， $\arctan(1/\sqrt{n}) = \pi/4$ ，碰撞总次数为 3。而当两个滑块质量悬殊时， $1/\sqrt{n}$ 就很小，此时 $\arctan(1/\sqrt{n})$ 就可以直接用 $1/\sqrt{n}$ 来近似，于是碰撞总次数就约为 $\lfloor \sqrt{n} \,\pi \rfloor$ 。当两个滑块的质量之比 $n$ 是 100 的幂时， $\sqrt{n}$ 就是 10 的幂，这就难怪碰撞总次数会恰好是 $\pi$ 的前若干位了。

来源：知乎 www.zhihu.com
作者：王赟 Maigo

【知乎日报】千万用户的选择，做朋友圈里的新鲜事分享大牛。点击下载

经典网文分享

11220 一道弹性碰撞的物理题，结果为什么会出现 π ？

没有评论:

发表评论