经典网文分享

【CFT01】度规初步

本学期参加了一个共形场论的研讨班，为了变成一个合格的名词党所以做一些相关的读书笔记。本文主要介绍了微分流形以及度规张量的概念，以及举了一些常见的例子，用以为后续的讨论的共形场论提供数学基础。本系列主要参考Paul Ginsparg的应用共形场论教材[1]，本文还参考了梁灿彬的广相教材[2]。

我们先复习微分流形的概念。直观上，我们研究一个光滑的空间，其任意小邻域都和欧氏空间类似。数学上，一个 $C^\infty$ 微分流形是一个（维的）拓扑空间，其满足：

其是Hausdorff空间，即任意两点可被它们的邻域分离；
存在维局部坐标邻域（在拓扑上是开集），即对任意给定流形上的点，存在其的一个邻域和一个映射 $\varphi: U\rightarrow U'$ （这里是 $\mathbb R^n$ 上的一个开集），使得 $\varphi$ 是同胚（连续双射且反函数连续），另外有序对族 $\{(U_\alpha,\varphi_\alpha)\}$ 被称为该流形的图册（atlas）, $\alpha$ 被称为索引；
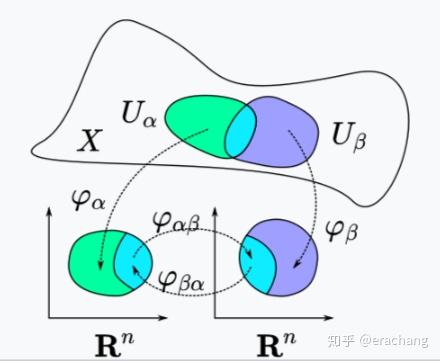
其图册的转移映射（transition map）是光滑的，如图所示， $U_\alpha$ 和 $U_\beta$ 是两个有重叠部分的开集，它们分别同胚于 $\mathbb R^n$ 上的开集，而重叠部分在 $\mathbb R^n$ 上的两个像之间的映射 $\varphi_{\alpha\beta}$ （或其逆映射 $\varphi_{\beta\alpha}$ ）叫转移映射。

最简单的微分流形就是 $\mathbb R^m$ 本身，黎曼球面 $\mathbb S^2$ 也是常见的微分流形。直观上一个微分流形可以嵌入到一个更高维的欧几里得空间中，而对于流形上的一点，在其上和流形相切的欧几里得子空间即其切空间（tangent space）。

然而基于更高维平直空间嵌入的定义方式并不是最好的定义切空间的方式。为了定义流形上的切空间，我们先观察 $\mathbb R^n$ 上的向量，其具有长度、方向，但这些概念很难在流形上推广。注意到若 $\mathbf v$ 是一个向量，则对于任意函数 $f:\mathbb R^n\rightarrow \mathbb R$ ，让其在一点上沿 $\mathbf v$ 方向上求导，其导函数值等于某个实数。故 $\mathbf v$ 是 $\mathbb R^n$ 上所有光滑函数的集合到实数的映射，且其服从线性和莱布尼兹率。

【切空间】称 $f:M\rightarrow \mathbb R$ 是流形上的一个 $C^\infty(M)$ 函数，若对于每组 $\{U,\varphi\}$ 都有 $f\circ\varphi^{-1}: \varphi(U)\rightarrow \mathbb R$ 是光滑的。对于 $x\in M$ ，称映射 $\partial:C^\infty(M)\rightarrow \mathbb R$ 为上的导数，若其满足莱布尼兹率即 $\partial(fg)=\partial(f)g+f\partial(g)$ 。如果再者我们定义导数的加法和数乘满足线性，即 $(\lambda \partial_1+\partial_2)(f)=\lambda \partial_1(f)+\partial_2(f)$ ，我们则有一个由所有导数组成的线性空间，称处的切空间。

对于一个光滑流形上一点，其邻域上有映射 $\varphi=(x^1,\cdots,x^n):U\rightarrow \mathbb R^n$ ，其中 $(x^1,\cdots,x^n)$ 是一组 $\mathbb R^n$ 的基底，则可以对应地在切空间 T_xM 上定义一组基底 $(\partial_{x^1},\cdots,\partial_{x^n})$ 满足

$\partial_{x^i}(f)\Big|_{x}:=(\partial_{i}(f\circ\varphi^{-1}))(\varphi(x)),\forall f\in C^\infty(M)\\$ 即对对应的 $\mathbb R^n$ 上的光滑函数在第个分量（即方向 x^i 上）求导，那么对于任意的切向量我们可以找到一组线性组合满足 $v=\sum_iv_i\partial_{x^i}$ 。

为了研究微分流形的距离结构，我们需要研究其线元素（或称第一基本形）。直观的理解是流形上一点附近的一段微小的长度（的平方），即欧几里得平面上的 $\Delta s^2=\Delta x^2+\Delta y^2$ 。我们可以考虑将每个方向上的微元放缩一个倍数，比如 $\Delta s^2=\Delta x^2+1/2\Delta y^2$ ，即在轴上的距离变化比轴上的距离变化"更短"，这类似于一个圆柱面。于是，对于非欧的流形上的推广，我们希望将线元素定义为 $\mathrm dx^2_i$ 的线性组合，"尽可能不"出现交叉项 $\mathrm dx\mathrm dy$ ，又或者考虑变换坐标系对其的影响等。

我们的动机是需要构造形如 $\mathrm ds^2=\sum_i a_i\mathrm dx_i^2$ 的量，则需定义度规张量（metric tensor，或简称度规）来定义上述的 a_i 。形式化的理解度规是对"给定坐标的" 维微分流形上，每一点都对应的一个 $n\times n$ 的对称、满秩的矩阵，该矩阵可以描述该点附近空间的距离结构。严谨的定义如下：

【度规张量】是微分流形，是其上的一点，其切空间为 $\mathrm T_xM$ 。上的一个度规张量 $g_x:\mathrm T_xM\times\mathrm T_x M\rightarrow \mathbb R$ ，将两个切向量映到实数，且满足：
1. 双线性，即等；
2. 对称性，；
3. 非退化性， $\forall X\ne 0, \exists Y \text{ s.t. }g(X,Y)\ne 0$ 。
另外我们还要求是光滑变化的，即对于给定邻域内的光滑向量场和，关于光滑。

注意到有限维线性空间上的双线性映射都可以由矩阵描述，故度规也可以由矩阵给出表述。

为了方便我们先引入简化记号 $\mathbf a\cdot\mathbf b =a_jb^j=\sum_{j=1}^na_jb^j$ ，这里上标不是指数而是标号。

现在假设我们在切空间上有一组基 $\mathbf e=(e_1,\cdots ,e_n)$ （ $\mathbf e$ 是一个 $n\times n$ 的矩阵），则我们定义 $g_{ij}[\mathbf e]=g(e_i,e_j)$ ，其构成一个 $n\times n$ 的矩阵，记为 $G[\mathbf e]$ 。假设另外有两个向量 v=v^ie_i, w=w^ie_i （意为列向量 $(v^1,\cdots,v^n)^\top$ 和 $(w^1,\cdots,w^n)^\top$ ），由双线性我们有 $g(v,w)=v^iw^jg_{ij}[\mathbf e]$ ，写成向量和矩阵的形式即 $g(v,w)=v^\top Gw=w^\top Gv$ 。同理对于线性变换 $\mathbf e\rightarrow \mathbf eA$ ，度规的变换为 $G[\mathbf e A]=A^\top G[\mathbf e]A$ 。注意到由于上述向量都是切向量，即 $\mathbf e=\left(\partial_{x^1},\cdots,\partial_{x^n}\right)$ ，故线性变换实际上是雅可比矩阵，即 $a_{ij}=\partial_{x^i}y^j$ 。另外，由对称性可知矩阵是对称的，由非退化性可知 $\det G\ne 0$ 。

度规具有矩阵结构这个性质可以很方便地让我们研究其上的各种性质，对称性允许我们对其求特征值，非退化性保证了特征值不为0，进而定义度规的符号（signature）：

【符号】（满秩）矩阵的符号为一个二元组，分别代表其正负特征值的个数。

注意到符号具有旋转不变性，即不取决于基的选择，故可以定义度规（在一点处）的符号数。另外度规的符号实际上是某种广义对流形的衡量：

若是单连通的，其度规的符号不取决于点的选择。

对于单连通的微分流形，若的符号是 (n,0) ，我们称该流形为黎曼流形，否则称为伪黎曼流形。一个重要的伪黎曼流形的例子是洛伦兹流形，其符号为 (p,1) 。通常在物理上，我们把看成类空维度，看成类时维度，另外如果是退化的，我们把特征值等于0的维度称为类光维度。

现在线元素（line element）或者其平方第一基本形（first fundamental form）可以被定义为：

$\mathrm ds^2=g_{ij}\mathrm dx^i\mathrm dx^j$ 。

我们总是可以对度规张量求特征值，使得第一基本形不包含交叉项，即若的特征值是 $\{\lambda_i\}$ 则 $\mathrm ds^2=\sum_i\lambda_i\mathrm dx^2_i$ ，即直观理解将每个方向上的"长度"放缩了一个倍数。则可知对流形上的一条曲线，对其参数做积分即可求得其长度，即 $L_{ab}=\int_{a}^b\sqrt{\mathrm ds^2}$ 。故此，我们说度规张量描述了流形的距离结构。再者，我们可以用度规定义体积形式（volume form）：

$\omega=\sqrt{|\det g|}\,\mathrm dx^1\wedge\cdots\wedge\mathrm dx^n$

直观上理解假如我们将基底正交化为的特征向量方向，则变成一个对角阵，则体积形式简化成 $\prod_i\sqrt{\lambda_i}\bigwedge_i\mathrm dx^i$ ，这与欧氏空间的体积微元定义相符 $\prod_{i}\Delta x^i$ ，区别是在每个方向上做了放缩。另外任何体积形式都定义了该空间上的一个波莱尔测度 $\mu(U)=\int_U\omega$ ，但进一步为了定义波莱尔测度我们不需要流形的连续性和光滑性。

下面我们来讨论一些例子：

二维欧几里德流形。在笛卡尔坐标系下其度规为单位矩阵，对应的线元素为 $\mathrm ds^2=\mathrm dx^2+\mathrm dy^2$ 。若我们把坐标变换成极坐标系，度规 $g=J^\top J=\mathrm{diag}(1,r^2)$ 其中是雅可比矩阵，即 $\mathrm ds^2=\mathrm dr^2+r^2\mathrm d\theta^2$ 。
四维洛伦兹流形。线元素是 $\mathrm ds^2=\mathrm dx^2+\mathrm dy^2+\mathrm dz^2-c^2\mathrm dt^2$ ，其中是光速，其有三个类空维度和一个类时维度。若将它转换成球面坐标我们有 $\mathrm ds^2=-c^2\mathrm dt^2+\mathrm dr^2+r^2\mathrm d\Omega^2$ 其中 $\mathrm d\Omega^2=\mathrm d\theta^2+\sin^2\theta\mathrm d\phi^2$ ，后者是 $\mathbb S^2$ 上的一个标准度量。计算并不复杂，我们写出 $\mathbb R^3$ 中球坐标变换公式 $x=r\sin\theta\sin\phi\\y=r\sin\theta\cos\phi\\z=r\cos\theta$ 然后对其求雅可比矩阵 $J=\frac{\partial(x,y,z)}{\partial(r,\theta,\phi)}$ ，则 $G=J^\top J$ ，我们用Mathematica辅助计算易得结果 $\mathrm ds^2=\mathrm dr^2+r^2(\mathrm d\theta^2+\sin^2\theta\mathrm d\phi^2)$ 。最后需要把空间限制在单位球面上，即对 $\delta(r^2-1)$ 做积分得 $\mathrm d\Omega^2$ 。

JacobianMatrix[f_List?VectorQ, x_List] :=   Outer[D, f, x] /; Equal @@ (Dimensions /@ {f, x})(*define Jacobian matrix*) cartesian = {r*Sin[t] Cos[p], r*Sin[t] Sin[p], r*Cos[t]}; sphere = {r, t, p}; J = JacobianMatrix[cartesian, sphere]; FullSimplify[MatrixForm[Transpose[J].J]]

我们有3维得欧几里德空间得（平直）度量，用极坐标表示为 $\mathrm ds^2=\mathrm dr^2+r^2\mathrm d\Omega^2$ 。对于 $\mathbb S^3$ ，我们将其嵌入 $\mathbb R^4$ 并考虑其坐标 $(R,r,\theta,\phi)$ ，其中后三个分量是一个三维球坐标，描述了子空间 $\mathbb R^3$ ，而是该四维向量的长度，则坐标变换如上述的球坐标以及第四个分量 $w=\sqrt{1-r^2}$ ，然后把它们缩放倍，则求得该坐标下的度量为 $\mathrm{diag}(1,R^2/(1-r^2),r^2R^2,r^2R^2\sin^2\theta)$ ，最后对delta函数 $\delta(R^2-1)$ 做积分我们有度量 $\mathrm ds^2=\frac{1}{1-r^2}\mathrm dr^2+r^2\mathrm d\Omega^2$ 。类似地我们考虑三维马鞍面，将其嵌入伪欧几里得空间 $\mathbb R^4$ 中，度量为 $\mathrm ds^2=\mathrm dx^2+\mathrm dy^2+\mathrm dz^2-\mathrm dw^2$ ，类似地考虑变量代换 $(x,y,z,w)\rightarrow(R,r,\theta,\phi)$ ： $x=Rr\sin\theta\sin\phi\\ y=Rr\sin\theta\cos\phi\\ z=Rr\cos\theta\\ w=R\sqrt{1+r^2}$ 并计算其度量 $J^\top GJ=\mathrm{diag}(-1,R^2/(1+r^2),r^2R^2,r^2\sin^2\theta)$ ，对 $\delta(R^2-1)$ 求积分可得度量 $\mathrm ds^2=\frac{1}{1+r^2}\mathrm dr^2+r^2\mathrm d\Omega^2$ 。我们发现它们可以统一到一个框架下： $\mathrm ds^2=\frac{1}{1-Kr^2}\mathrm dr^2+r^2\mathrm d\Omega^2\\$ 其中 $K\in\{-1,0,1\}$ 。这就是宇宙学上FRW度规（Friedmann-Robertson-Walker metric）的一个组成部分，完整的FRW度规需加上时间维 $\mathrm dt$ 以及宇宙标度因子 : $\mathrm ds^2=-c^2\mathrm dt^2+R(t)^2\left(\frac{1}{1-Kr^2}\mathrm dr^2+r^2\mathrm d\Omega^2\right)\\$

参考文献：

[1]: Ginsparg, Paul. "Applied conformal field theory."arXiv preprint hep-th/9108028(1988).

[2]: 梁灿彬, 周彬. 微分几何入门与广义相对论. 科学出版社, 2006.

来源：知乎 www.zhihu.com
作者：erachang

【知乎日报】千万用户的选择，做朋友圈里的新鲜事分享大牛。点击下载

会多种语言是什么样的体验？

Lowry said I can't speak English, then I answered questions in English, French, and Spanish. Maybe I could add Lingala the next time. lol

来源：知乎 www.zhihu.com
作者：伊巴卡

【知乎日报】千万用户的选择，做朋友圈里的新鲜事分享大牛。点击下载

此问题还有 202 个回答，查看全部。
延伸阅读：
为什么口音一旦形成，就很难改变？
使用不同的语言，会对人们的思维方式产生怎样的影响？

绝地求生和彩虹六号中的枪口背后作用原理

大家玩了那么多射击游戏，对于游戏中各种枪口的作用肯定非常了解。

但你有没有想过，在真实的武器上这些枪口的作用原理？

制退器为什么能减后坐力，消焰器为什么能消除枪口火光，消音器为什么能消音。

本期节目承载《彩虹六号：围攻》和《绝地求生》，讲述游戏中的枪口背后的作用原因。

https://www.zhihu.com/video/978223004983918592

感谢各位对《不止游戏》节目支持，我是《不止游戏》节目UP主 Joey乔伊

《不止游戏》节目秉承"游戏不止，不止游戏"的宗旨。旨在挖掘游戏背后的真实历史，故事，有趣的细节。探究优秀游戏更深层次的含义。

欢迎大家关注，点赞支持。

如有意见和建议可以私信或者留言评论区。

来源：知乎 www.zhihu.com
作者：SONAR森纳映画

【知乎日报】千万用户的选择，做朋友圈里的新鲜事分享大牛。点击下载

白发显老，怎么才能让白了的头发“黑回去”？

作者：圆子医大脑

仔细回忆了一下，我的前半生遇到了很多小伙伴，和我一般年纪，已经早生华发。

据说头发白得早的小同学成绩好，自古学霸多白发，emmmmmm…...

天生丽质没白发的我，决定来给大家讲一讲白头发的那些事。

一. 什么决定了头发的颜色？

头发的颜色由两种类型的黑色素决定，分别为真黑素(eumelanin）和褐黑素(pheomelanin）。

通常，真黑素多头发就呈黑色或棕色；褐黑素越多头发颜色越浅，呈红色或黄色。

两种黑色素的共同作用，是不同的人拥有不同发色的原因。即使在同一个人身上，不同的毛囊也可能生出不同颜色的头发。

二. 什么让你年少却白头？

头发变灰变白是因为真黑素细胞受损，人尽皆知的影响真黑素细胞的因素是年龄。随着年龄增长，头发的颜色会变灰甚至变白，这被称为毛发褪色（achromotrichia）。

每个人都会经历白头，但大多数人发生在40岁或50岁之后，这受到遗传学、性别和基因的影响。

话虽如此，却有越来越多的年轻人开始长白头发，这就是"少白头（premature greying），亚洲人25岁之前出现白发就可以被称为少白头。

目前，少白头的机理还未完全清晰，可能因素有：

疾病因素

恶性贫血、甲亢或甲减、早衰症，或者哮喘、接触性皮炎等特应性疾病都会引起少白头；

心脏病也会引起少白头。

研究显示，灰/白发的严重程度与冠心病的病情有相关性。如果你患有心脏病，头发突然变白了，那可能是心脏病变化的迹象。

药物因素

服用氯喹、甲苯丙醇、三苯乙醇、表皮生长因子受体抑制剂、α干扰素等药物也有可能让头发变白。

营养素缺乏

严重或慢性的蛋白质、铁、叶酸、维生素B12和铜缺乏会导致少白头，

除此之外，在少白头人群中，钙、维生素D和铁蛋白含量都很低。

二战期间，集中营内许多无法满足营养需求的人都出现了长白发的情况。

压力山大？

一些人认为压力是导致少白头的重要原因。

但事实是，压力并不能影响黑色素让头发"变"白。

通常情况下，年轻人掉发后长出的还是黑发，但压力会使人的脱发掉发更严重，大量掉发后的新生发可能正巧赶上了该长白发的那一茬，给人一种一夜白头的错觉。

环境因素

2006年的一项研究显示，某些对DNA有毒性的自由基可能使细胞老化甚至杀死细胞，其中就包括了真黑素细胞。

环境污染、紫外线、炎症都会增加自由基。

吸烟也能增加体内自由基，被证实与少白头有相关性。

但目前为止还没有对照实验来证实自由基与少白头间相关性的阐述。

三. 白了的头发还能黑回去吗？

这个因人而异。

医生通常会先找到白头的原因，检查你是否缺乏营养素、服用了哪些药物、是否有自身免疫性疾病等。

如果只是因为营养缺乏或者药物的影响，那还是有治疗的可能性。

但总体来说，治疗的结果让人失望。

目前有一些口服类药物，但成功的案例很少。也有一些药物服用后可以使头发变黑，但是停药2-4周后便会复发。

数据显示，少白头对患者的心理造成了很大影响，因此，常常有患者随意服用保健品以期获得效果，然而迄今为止，公开文献中关于其功效的科学证据水平还很低。

已成白发的无法回头，我们能做的只有减缓恶化。

白发通常比黑发更粗硬更难上色更难打理，这里有一些日常护发小建议：

不要经常吹白发，自然干是对白发最温柔的方式。
不要经常拉直，热会让头发变白变卷。
不要烫发。
不要把钱浪费在宣称会让你头发黑回来的洗发水护发素上。
不要在日光下暴晒。因为白发缺少黑色素，它们无法阻挡紫外线的伤害。
安全染发。尽管目前还没有证据能证明使用染发剂与癌症之间存在关联，但染发剂的刺激性可能会导致过敏、发炎或脱发。

长白发的小伙伴不要太在意，不就是头发颜色不同寻常嘛，也没什么大不了的！

比如春雨的小编想染奶奶灰却染出了一种不可描述的颜色......

请看 ↓ ↓ ↓

参考资料：

1. Pandhi D, Khanna D. Premature graying of hair.[J]. Indian J Dermatol Venereol Leprol. 2013, 79(5):641-653.

2. Kocaman S A, Çetin M, Durakoğlugil M E, et al. The degree of premature hair graying as an independent risk marker for coronary artery disease: a predictor of biological age rather than chronological age[J]. Anadolu Kardiyol Derg, 2012, 12(6):457-463.

3. https://www.nytimes.com/2017/06/09/well/live/why-does-hair-turn-gray-at-a-young-age.html

4. https://en.wikipedia.org/wiki/Human_hair_color#Effects_of_aging_on_hair_color

编辑：大王

题图来源：爱奇艺截图

来源：知乎 www.zhihu.com
作者：春雨医生

【知乎日报】千万用户的选择，做朋友圈里的新鲜事分享大牛。点击下载

NBA 17-18 赛季西部季后赛决赛勇士 vs 火箭，谁会胜出？为什么？

火箭昨天112-102战胜了爵士，球队顺利打进西决。本场比赛双方基本还是维持过去的战略打法，只是火箭在完成和执行上要好过爵士，所以也没什么好说的。不过从内容上看，这场比赛是属于保罗一个人的，41分7板10助攻，是他帮助自己和火箭打进西决，他们即将面对的是强大的勇士队，下面我们就来聊聊关于两支球队的展望。

我先说说我的看法吧，我认为勇士和火箭的赢球面分别是5.1和4.9，至少从今天两支球队在场面上展现出来比赛质量我是这样看的，两支球队非常接近，但是勇士要稍微占优。所以第一场对于两队来说都非常重要，如果火箭赢了，那就是4-2或者4-3进总决赛，如果输了可能就会被淘汰。

火箭和勇士都是善于寻求空间的球队，但是勇士的空间更大，拉的更开，因为他们的投手更准、更高、射程更远。我们以库里、汤普森、杜兰特作为勇士的投手代表，这三个人的赛季三分命中率分别是42.3%、44%、41.9%。火箭的三分投手代表是哈登、戈登、保罗（有人可能说安德森也可以呀，但是目前不确定他是否能否有出场时间，确定上场的话就另说了），他们三个的赛季三分命中率分别是36.7%、35.9%、38%。可以看出命中率是有差距的，身高上就不用我再描述了。除此之外，勇士的射程更远，因为无论是克莱、库里还是杜兰特，几乎不看三分线的距离，在前场接到球出现机会就一定会投篮。可是火箭除去哈登和戈登外，保罗是喜欢踩着三分线投篮的（我不是说保罗的三分踩线），除非被逼到一定地步。注意，这是一个细节，当保罗距离三分线一步远时他的防守者都喜欢给他半步的距离，因为他们赌保罗不会投，这也防止了被保罗一步过掉。所以勇士的外线比火箭要稍微占优的。

对于火箭来说，他们除了主场优势和常规赛2-1这些之外，就是哈登一定要发挥，他一定要把他的一二三分都拿到手。保罗今天的发挥给了火箭极大的想象力，他的好胜心、求胜欲望在所有人之上。本赛季单打成功率哈登和保罗排在联盟前三（还有个人就不用我说了），勇士在传球和投射方面胜过火箭，但是篮球比的谁最后能把球送进篮筐，所以火箭虽然外线射手不如勇士但不代表他们的进攻比勇士差，那么防守对于两队就显得格外重要。

本赛季火箭的防守策略是无限换防，当卡佩拉在场时火箭的篮板、盖帽等内线的保护上肯定要做的更好，但是问题在于勇士的死亡五小都拉在外面，空间拉的非常大，卡佩拉是否具备在三分线外两米的防守能力？如果这时候对手选择突破以他的速率能否跟的上是个问好？？？如果火箭换下卡佩拉由塔克出任中锋时，他们的身高吃亏，不过火箭靠着他们的死亡五壮也并非没有赢过勇士的死亡五小。所以，我觉得卡佩拉会是火勇对决的X因素！那么勇士的死亡五小有没有弱点呢？当然有，就是错位让哈登单打库里！前面说了哈登必须发挥，有一部分也是这个原因。

综上，两队实力非常接近，所以我想双方教练不会让比分拉大到8分才叫暂停，甚至是4-6分就要叫暂停，胜负很有可能只是一个回合的事，谁能抓住机会，利用好阵容的优势谁就会赢。对于我们来讲，期待西决吧！

来源：知乎 www.zhihu.com
作者：马健

【知乎日报】千万用户的选择，做朋友圈里的新鲜事分享大牛。点击下载

此问题还有 328 个回答，查看全部。

女生租房子要注意哪些问题？

女性朋友尽量不要独租

如果独租房怎么办：

一、看好房，验房带"保镖"----------------------------------------------

1、租房时找一个好一点的环境。交通便利的市区房租金相对要高一些，但如果工作晚回家时，也不用太担心。不要一味要求房租便宜就马虎租房。选择房屋的时候，要看房屋的采光，通风好不好，环境卫生怎么样，阴冷潮湿蟑螂遍地的房屋，价格再低也不能租住，对身体有影响。

2、可以最好找一个和朋友一起住的楼房，离的近了，有什么事也好有个照应。若是在人烟稀少的地方，就算遇到了坏人，也没人能帮上你。找一个好房东也很重要，要不然入住后好多事很麻烦。

3、不要轻信路边小广告。房屋中介公司虽然会收取一定得费用，但是相对正规一些。千万不要看路边的小广告，有很多是骗子的陷阱，一不小心中招了，骗取钱财到是小事，还可能危及性命。

4、租金过于低廉小心有猫腻。对于那些租金过于低廉的出租房，女生也要提高警惕。天上不会无缘无故的掉馅饼，大多数都是陷阱。贪这种小便宜的人，不是被骗财就是被劫色，女生一定要擦亮双眼多个心眼。多看看房东的身份证，房产证之类的证件。

5、最好不要独自看房。看房时最好有朋友相伴（男生为宜），最好在周末，房屋周边的邻居都在的时候，进屋时不要把门关上，以防遇到坏人无处可逃。

二、签合同，擦亮双眼-----------------------------------------------------

1、租房押金在租房合同中要标明退还事项。房东在租房给你的时候，一定会收取几百至几千不等的押金，说在退房时会给你。但是有些心怀不轨的人，会找各种理由借口扣留押金。女生在跟房东签租房合同的时候，要仔细阅读内容，以防有诈。最后要把全数退还押金也要明确写上去。

2、水电暖费用需要合同中写清楚。租房时候要问清楚水、电、煤气，家具、家电，物业费、卫生费、有线电视费、宽带费等等，有些粗心的女生就忽略了这部分，导致最后需要自己全数买单。建议女生们在租房时要跟房东协商好，必要的时候要签在合同中，费用是如何承担要写的清清楚楚。

3、检点房间物品数量，是否有损坏。对房东提供的物件，应该清楚地记录在合同中。还要检查所有东西是否可以正常使用，各种电器，用具，检查有无破损，避免日后引起纠纷。

4、签订租赁合同，保管好合同和付款的单据。对于中介，一定要注意中介公司是否与原房东签署了"房屋租赁代理合同"，合同中是否有原房东允许中介代办房屋租赁手续、并代收房租的条款。如果中介只是把房屋承租下来，并没有告知原房东自己要溢价转租。原房东一旦要求收回房屋，租客和中介签署的租房合同将变为无效，租客最后只能被迫搬家，再去追究中介的责任。

三、独居带上安全意识-----------------------------------------------------------

1、若要找合租者，在网络上发布合租信息的时候别将自己的真实信息暴露太多。

2、对收水电费、送煤气、送快递等人员一定要仔细核查身份再让对方进房。

3、避免与左邻右舍关系过好而降低危机意识。轻易透露房内贵重物品或钱财更是不可取的。

4、如遇小偷不要慌张，夜间不要大喊避免激怒窃贼。白天或着开着窗门，那么就要大声喊叫吓住窃贼；但如果是夜间，又赶上楼道内无人，尽量不要叫喊避免激怒窃贼。

5、独自回家要留意身后有没有可疑的陌生人跟踪。如果感觉后面有人跟着，无论是路人甲还是可疑的陌生人，都尽量寻找机会让对方走在前面，避免危险。回到家准备开门时要注意看周围有没有人，要以最快的速度开门并关上。

6、记住房东的电话还有离你最近的派出所的电话。万一有什么紧急事情，可以就近求救。

7、最好购置一两样防身武器，如防狼喷雾或强光电筒等。若真遇窃贼或打劫的，没更好办法的情况下，宁舍钱财，保重安全。

8、家中常备药箱。夜里突然肚子疼的时候，没有人下楼为你买药。

9、个人外出频繁，会很容易让不法分子盯上，所以可以不定期的请自己的好朋友(值得信赖的朋友，最好是你对他知根知底的人)来玩上两天。

10、不要带刚认识的人回家，不是太熟的朋友也不要带回家，不要让他知道你家里的详细位置。

11、不要在入睡后接电话，即便是熟人也不要接。因为往往深夜打电话的都是有事的。

12、最好在平时有锻炼健身，这样有什么危险时，可以不让自己受太大的伤害。

,13、要有能处理一般的家务能力。比如：换电灯泡、打扫天花板、修理水管等等。因为是自己一个人生活，会很寂寞，可以给自己安排很多节目，让每天的生活丰富多彩。

14、如果遇到歹徒拎包，就把包给他们，和他们好好商量，也许还可以把钱财除外的东西拿回来。

15、如果晚上有人入室盗窃，不要慌张，就当做没看见，继续睡觉。可以把男孩的衬衣、短袖放在阳台上，制造一个假象，让其知道家里的男孩。记住房东的电话还有离你最近的派出所的电话。邻里之间见面可以多打招呼，时常微笑待人，与邻居大妈们搞好关系。

16、家中发现断电现象，不要急忙把门打开，小心有人故意为之。钥匙，是单身女性租房很容易丢失的东西。常备几把钥匙，放在信任的人那里一把，公司一把，都是重要的。

17、防火要注意，家中的电源开关，充电器，厨房用品都需要谨慎使用。自身的手机要随时处于畅通的状态，尤其是晚上，让别人可以随时找到你。可以准备一个小夜灯，安稳的睡个好觉。

18、外出时要关好门窗，确定都关好了再出门。至少有1个当你忘记拿家门钥匙时可以去借宿的朋友。

19、一个人在外面生活或多或少都会觉得孤单，尤其是晚上一个人在家，白天还有工作学习，夜晚却只有一个人。不要害怕也不要担心，放轻松。可以做一些运动或自己喜欢的，帮助睡眠。没事了往家打个电话，你心里就不那么孤单了，家长也放心了。

来源：知乎 www.zhihu.com
作者：夏道好

【知乎日报】千万用户的选择，做朋友圈里的新鲜事分享大牛。点击下载

此问题还有 17 个回答，查看全部。
延伸阅读：
怎么花最少的钱提升出租屋的格调？
租一辈子房会不会后悔？

订阅：博文 (Atom)