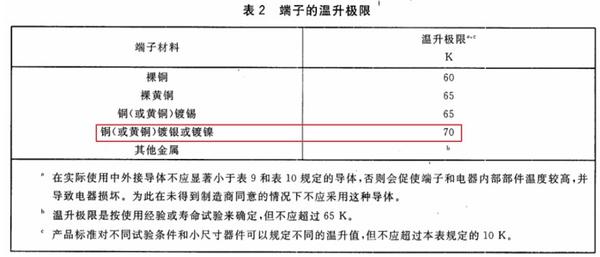
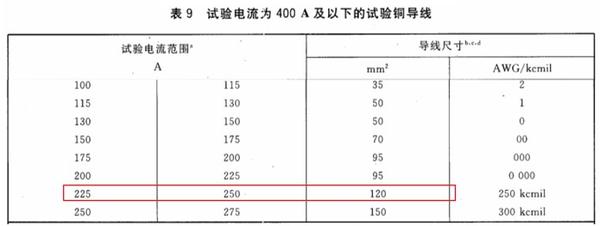
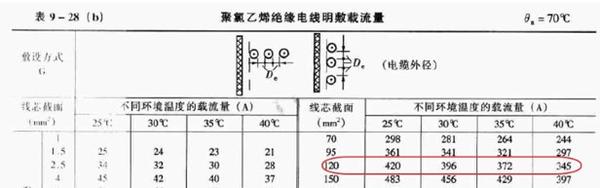
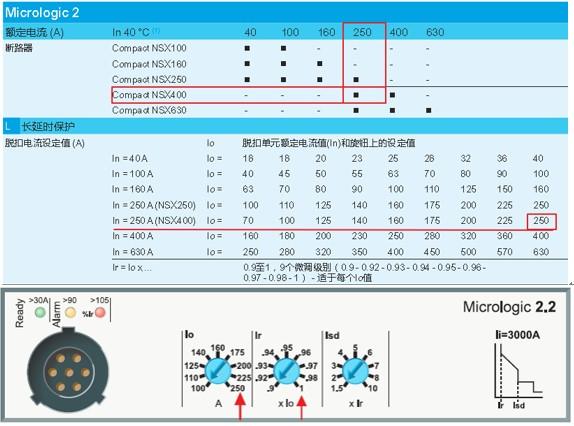
(估计这图你们都看烦了,下次我试图换一个……)
大家好!
因为知乎在版本升级的时候出现了意想不到的bug(草稿内容再一次打开会被清空),导致我之前的笔记丢失,损失惨重,所以二三章的笔记整理的内容不会出现在这一系列笔记中,目前我有一些给大家补救的方案,已经专门写在了这里,大家可以看一下:
刘理:杂烩|2018.5-近期情况说明,相关typo修改这一章是Prof习题课的内容,针对了二三章较难或者重要的习题进行了一些整理。
提供之前的笔记:
我们开始本节的内容。本节是复习章节。
Exercise 1:
设,令
,求
。
根据"可数集的测度为零"的结论,我们可以自然考虑这个集合的另一面。首先根据 可以得到
,之后再考虑
,把集合改成
,其中
。关注重点自然在
上。
注意到 ,所以
在题目给定区间上是一个单减函数,那自然就可以考虑将它的每一个值与区间
上的有理数一一对应。设
,并且记
,也就是
。那么显然根据
函数的图像,容易得到对于每一个固定的数,这个集合在平面上都是一条线段。注意到
,所以它是可数个这样的线段的并。又因为线段测度为0,所以自然得到
,进一步有
。
Exercise 2:
设为
的递减可测集列,
。令
,
,证明
。
这是一个递减集合列,我们在书上有一个结论是说,递增集合列的测度和极限运算可交换。所以可以考虑构造递增集合列。那么自然就是考虑 ,也就是
。所以根据集合的运算,容易得到
。
接下来怎么办?因为集合的可测性并不清楚,所以要考虑的自然是可测集的定义,因为可测集的定义能够构造一些有用的外测度的等式。考虑集合 ,它们都是可测集,所以根据定义有
,并且有
。但是注意到第一个式子取极限,可以得到的是
(用了刚开始的结论)。是不是看着有一项已经一样了?最后再根据
外测度有限即可得到结论。
Exercise 3:
设为
中的不可测集,证明存在
,使得对任意的
中满足
的可测集
,有
不可测。
这里考虑的是"零测集可测"的结论。因为这个结论成立,所以可以考虑当 的时候是否会出现反例(因为这个时候,另外一边集合的测度就趋于0了)。因此反证法是必需的。
如果对于任意的 ,存在
,并且有
,使得
。那么这样的话,考虑取
,这样的话,因为
,所以有
,所以
。
记得关于等测包结论的证明吗?我们构造出了一系列的集合它的测度趋于0,那么自然考虑的就是取 。这样的话,首先
,其次
。并且容易得到的是
,也就是
。
这会出现什么问题?别忘了, 不可测,但是
,这就矛盾了。
Exercise 4:
设为
上一个连续函数族,则函数
在
上可测。
要想证明一个函数可测,只要说明 是可测集即可。也就是说,对于任意的
,都会存在
,使得
。
注意连续函数的条件。通过这个条件可以得到存在 ,使得任意的
,都有
。这说明什么?这就说明了
是一个开集,那它自然可测。
显然这里如果把 改成
结论也是成立的,证明也是类似的。
Exercise 5:
设有指标集,且
是
上的可测函数族,判断函数
是否在
上可测。
是否可测呢?事实上既有可能可测,也有可能不可测。可测的例子上面那个题就是一个,而不可测的例子要稍微难一些。
取 是一个不可测集,那么设
,这显然是可测函数(因为单点集可测),但是
是什么呢?注意到如果
,那么显然
,如果
,就可以得到
,也就是说
。这是一个不可测集上定义的特征函数,所以自然不可测。
Exercise 6:
设在
上存在右导数,证明右导函数
为
上的可测函数。
这个题要使用的结论是"几乎处处连续的函数可测"的。首先注意到表示 ,也就是说每一个点的右连续点是存在的。这样的话根据第一章例12(原书P20)的结论即可得到
的不连续点为一个可数集,那么也就是说
几乎处处连续。那么自然可测。这样的话,因为
可测,那么自然
可测,进而即可推得
可测,就证明了结论。
Exercise 7:
设为
上几乎处处有限的可测函数,
,证明对于任意的
,存在
上的有界可测函数
,使得
。
这个题有两种方法,我们分别写在下面。
第一种方法,考虑 ,那么根据这个构造可以得到
是一个递减序列,并且
,其中
。那么根据
可以得到
。也就是说
,存在
,使得
。
因为我们的 的目的是把无界的部分"挖掉",所以只需要在有限的区域上做定义就可以了。令
。那么这个就是满足条件的函数。
第二种方法是考虑Lusin定理。首先构造 ,那么这样的话,对于任意的
,存在
,使得
(这是因为这个构造在
的时候一定可以做到
)。又因为
为几乎处处有限的可测函数,所以根据Lusin定理,存在闭集
,使得
。并且
是连续的。现在只需要令
,那么自然会有
也是一个连续函数,这样就可以得到有界性。并且也不难证明它是满足条件的。
事实上,这个题就是要构造一个和原来的函数"差不多"的函数,因此根据这个结论想到的两个方法都是有源头的。第一个方法是考虑挖掉"无界"的部分,通过函数几乎处处有限,来得到想要的结论。第二个方法是根据Lusin定理本身"挖掉一部分测度"的特性,结合连续函数的有界性来得到结论。
Exercise 8:
设为
上几乎处处有限的可测函数,且
,证明存在
,使得
,并且
在每一个
上都一致收敛于
。
这个结论显然要使用的就是书上的定理3.12(第三节的各个收敛定理务必记得滚瓜烂熟)。根据 ,可以得到存在
,使得
,并且
在
上一致收敛于
。这样的话,
自然满足结论,相信剩下的部分不难完成。
Exercise 9:
设为
上的可测函数列,
为
上的实值函数,如果对于任意的
,有
,判断
是否在
上可测。
首先,根据分解可以得到 (拆为
和
),也就是说
是一个依测度收敛的Cauchy列。那么根据定理3.16,可以得到,存在
在
上有限并且可测,使得
依测度收敛到
。这样的话根据同样的分解,可以得到
。那么这就是
几乎处处相等的意思,这样的话根据
可测即可得到
可测。
Exercise 10:
设为
上的实值可测函数,如果对于任意的
,有
,证明对于任意的
,存在
,
,使得
在
上一致收敛于
。
这个题目根据题目中给定的条件,容易想到的自然是引理3.11中的一些结论,它的证明中间的构造思想可以用在这里。
根据条件,对于任意的 ,有
(我觉得,你不应该再对这个构造表示陌生了),所以对于任意的
,存在
,使得
,那么我们自然考虑把里面这一串集合再并起来,也就是考虑
。
考虑并起来后,别忘了它的补集就是一致收敛含义的集合表示,也就是说,对于任意的 ,只要取
,即可得到对于任意的
,有
,(这个证明比较简略,更详细的细节读者可以自己完成)。
小结
这一节主要关注了原书的第二三章(测度,可测函数)的相关习题。要注意的是这一块的一些习题都是一些相对来说比较普适性的,看懂和独立解答这些习题后可以算是"过关"实分析的这一部分内容了。但是如果是要备战考试,可能还需要补充一些技巧比较独特的习题以作为积累。
——————————————————广告——————————————————

本专栏为我的个人专栏,也是我学习笔记的主要生产地。任何笔记都具有著作权,不可随意转载和剽窃。
专栏目录:笔记专栏|目录
想要更多方面的知识分享吗?欢迎关注专栏:一个大学生的日常笔记。我鼓励和我相似的同志们投稿于此,增加专栏的多元性,让更多相似的求知者受益~
来源:知乎 www.zhihu.com
作者:刘理
【知乎日报】千万用户的选择,做朋友圈里的新鲜事分享大牛。 点击下载