微信公众号:UGISER
城市技师 | UGISER
Urban Planning & Geographic Information System & Smart Design
序
首先解释一下此处为什么是"再说多规合一",早期关注我们公众号的小伙伴可能知道我之前发过两篇关于多规合一的文章,现由于公众号平台改版等多方面的原因,我已将旧文删除,并将以此文为基础,重新梳理技术框架并逐步推出相对完善的系列推文,欢迎大家关注共同交流探讨。
近日,国家机构改革,自然资源部的组建再次将多规合一推上行业舆论的前端,自然资源部在一定程度上将以前国土资源部、住房和城乡建设部等部门的众多职能进行重新整合,目的在于从顶层建立"多规合一"的机构保证,从而更加合理的对自然资源空间进行统一规划、管理和控制。
近些年各省市也在不断探索多规合一的技术方法和各种可能,尤其以沿海地广东、福建、海南等地走在多规合一探路的前沿,也积累了不少先进经验,笔者所在的重庆市也在2017年全面开展各区县多规合一编制工作,重庆市规划局也相应的发布了《重庆市"多规合一"编制技术指引(试行)》、《重庆市区县"多规合一"一张图编制技术指引(试行)》,《重庆区县"多规合一"成果数据库标准》等相关技术导则作为重庆市区县多规合一规划编制的技术要求和指导文件。
多规合一有别于我们传统的规划项目,它本身也不算是一个规划,更多强调的是"合一"的协调整合过程,包括不同部门、不同行业甚至不同阶段规划和管理事权的合一,做到同一空间、统一规划、统一管理,所以多规合一的前提在规划一张图,一切的规划要落到这一张图,一切的管理事权也是基于这一张图,只有这样才能避免空间规划冲突、规划管理打架的矛盾。
规划一张图表面看只是一张图,但背后确涉及复杂的技术和管理逻辑,本文基于重庆市多规合一的技术要求,梳理多规合一编制的总体思路和技术方法,抛砖引玉,以供同行交流探讨。
注:出于演示目的,本系列教程案例经过精简,重在讲解原理,某些规范细节不完全与技术指引要求相同,实际项目请严格遵循相关技术规范。
一、编制流程
根据技术文件要求,重庆市区县"多规合一"一张图编制工作首先由各区县制定编制计划,再由区县规划主管部门(规划局)组织编制单位充分收集整理各部门、各专业现状及规划等基础资料并绘制工作底图,在工作底图上进行多规用地差异对比,以此进行差异用地协调并形成"多规合一"一张图,作为下一步各专业规划调整修改的依据。
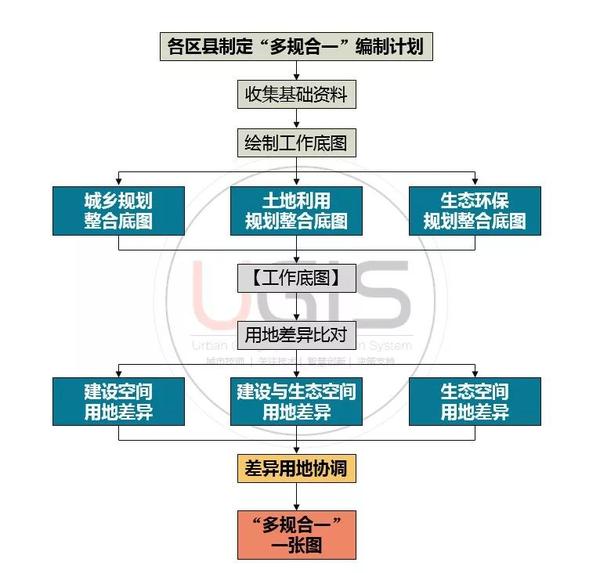 ▲"多规合一"一张图编制流程示意图
▲"多规合一"一张图编制流程示意图 二、 基础资料的收集
基础资料的收集本没什么好说的,跟传统规划的调研阶段资料收集基本无异,但是多规合一的资料收集更强调各类"规划"的收集。根据指引要求,多规合一收集资料主要包括基础地理信息资料和各类规划资料,其中基础地理信息资料包括卫星影像图、行政区界、电子政务底图等,各类规划主要包括城乡规划、土地利用规划、生态环境保护类规划和其他类可供参考的规划共四大类规划资料。
▼ "多规合一"基础资料收集表
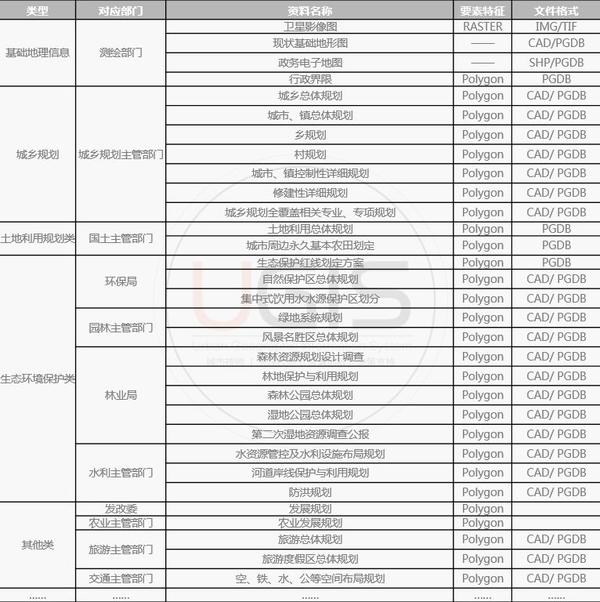
除以上区县级资料,还可能涉及到市级资料的收集,包括市域和跨区县相关规划,涉及市规划、国土、环保、林业、园林、水利等部门组织编制的相关规划;市级重大基础设施选址红线和市级储备土地红线等,具体由各相关分管部门协助提供。
三、工作底图的制作
一张图的总体原则就是梳理各专业专项规划中反应空间位置和范围的要素,并将其转化为统一标准、统一坐标的信息化基础数据,通过用地差异对比、协调后形成"多规合一"一张图,并搭建"多规合一"一张图数据库,以此作为后期空间规划编制、城乡规划管理的基础依据。
在绘制一张图之前需要对城乡规划、土地利用总体规划、生态环保规划进行梳理分别形成城乡规划整合底图、土地利用规划整合底图、生态环保规划整合底图。
3.1 城乡规划整合底图
根据城乡规划编制体系及《重庆市城乡规划条例》等相关规定,多规合一涉及到的城乡规划涉包括总体规划、详细规划及各类专业专项规划,城乡规划整合底图需要对区县域、城市、镇、乡等不同空间尺度下的各类规划进行整合。
(1)标准统一
按照《城市用地分类与规划建设用地标准》(GB50137–2011)对城乡用地进行统一分类,并建议统一图层名称。这里涉及到一个问题,就是先行的镇规划标准还是按旧版城市规划用地分类标准进行分类的,便于多规合一的统一,建议对城镇建设用地均按新的城市建设用地分类标准进行统一。
【TIPS】
注意区分城乡用地、城镇用地、城镇建设用地和农村建设用地
城乡用地:对应于城乡总体规划,是覆盖全域的一切用地,包括城市用地、镇(乡)用地、农村用地。
城镇用地:城市和镇(乡)用地,对应于城市、镇(乡)总体规划,是城市、镇(乡)规划区内的所有用地,包括建设用地和非建设用地。
城镇建设用地:城市、镇(乡)规划区内的建设用地,即我们控规所主要控制的用地,也是我们城市用地分类标准中主要确定的用地类别。
农村用地:可以理解为除了城市、镇(乡)规划区及各类区域性设施用地之外的用地。
注:以上解释说明只是为了便于直观理解,并非完全官方定义和分类,具体请查阅相关规范文件。
【END】
(2)坐标统一
由于不同尺度、不同时期的规划可能所采用的坐标系不一致,比如常见可能会遇到的情况就是区县域层面的城乡总体规划可能是采用的西安80坐标系,而城市及镇总体规划可能采用的是重庆独立坐标系,但是根据重庆市多规合一的技术要求,需要统一至2000国家大地坐标系,因此我们需要将不同坐标系下的各类规划数据统一转换至2000国家大地坐标系,根据重庆市的标准流程是统一由地理信息中心转换,但是从技术层面我们仍然是可以自行转换的,具体可参照本公众号的推文《说说坐标系和投影那些事儿》。
(3)规划统一
除了用地标准、坐标系等技术层面的统一,还应梳理各层级、各专业、各时期规划的冲突,如同一地块的总规和控规用地应该一致,专项规划和总规也应一致,只有将各类规划进行统一一致后才能进一步纳入整合数据库中。
(4)格式统一
传统城乡规划仍然是基于CAD的制图技术路线,成果大多数仍然是DWG格式的数字化文件,尤其是城市总体规划及控制性详细规划,基本都是CAD绘制,信息化水平低,无法进行多要素、多层次信息化对比,因此我们必须将其转换为ArcGIS支持的Shapefile文件格式,再将其统一导入"多规合一"一张图GDB地理数据库。
3.2土地利用规划整合底图
土地利用规划整合地图以土地利用总体规划图为基础,叠加永久基本农田划定方案等土地利用类规划,并标识有条件建设区范围、以地票或增减挂钩方式获得土地的范围等。
当前有较多土地利用总体规划成果为MapGIS数据文件,因此我们在制作多规合一过程中需要将其转换为ArcGIS支持的Shapefile文件,本文推荐使用FME工具进行转换,具体操作请关注本公众号,后期会推出专题文章讲解操作步骤。
3.3生态环保规划整合底图
生态环保规划整合底图主要是以生态红线为主体,整合叠加重要林地等生态资源空间,包括:自然保护区、森林公园、风景名胜区、饮用水源保护区、湿地、湿地公园、四山管制区、地质公园等的范围线及分级管控线;河道管理范围线、水利设施范围线、堤防工程岸线等;地质灾害范围线;绿地系统规划的各类绿地、I级、II级保护林地以及国家级公益林等。
以上各类生态空间数据往往涉及多部门,比如自然保护区、森林公园、风景名胜区归属林业、园林甚至旅游主管部门,饮用水源保护区、湿地、河道、水利设施等又规水利部门等,因此需要对多部门多元数据进行权威确定并最终整合为生态环保规划一张图。
由于数据来源于多部门,因此数据格式也可能存在多元的特征,如生态红线划定方案可以拿到Shapefile文件,但是像自然保护区、森林公园等其他数据的范围线就可能只能拿到CAD、JPG文件,或者只是一张拐点坐标点列表,甚至只是一段文字描述,这时我们就需要针对不同情况进行数据矢量化、定义并转换坐标、属性定义等信息化操作。
四、用地差异对比
用地差异的对比的目的是为了找出不同规划之间差异和冲突,以此作为差异用地协调的依据,其成果形式为用地差异对比图,分别包括建设空间用地差异图、建设与生态空间用地差异图、生态空间用地差异图。
4.1 建设空间用地差异
建设空间用地差异主要是对城乡规划(规划)整合底图与土地利用总体规划(国土)整合底图中的建设用地进行差异对比,并标识出建设用地的不同分布情况,以作为后期多规建设用地"合一"的基础依据。
两规建设用地对比分别有四种情况,分别为两规均为建设用地区域、土规为建设用地城规为非建设用地、城规为建设土规为非建设用地、两规均为非建设用地,针对这四种情况我们设置四种标识代码,方便后期建库,如下表所示。
▼建设空间用地差异对比标识代码表
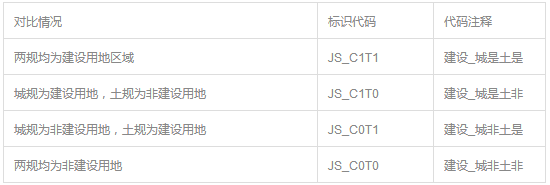
4.2 建设与生态空间用地差异
在城规、土规两规对比基础上,通过与生态环保整合底图进行差异对比,识别出建设用地与生态空间的冲突情况,根据建设用地对比情况,则一般包括生态空间与城规土规建设均有冲突、与城规建设有冲突土规建设无冲突,与城规建设无冲突土规建设有冲突、与城规土规建设均无冲突四种情况,同样的,我们针对以上对比情况设置四种不同的标识代码,方便后期建库,如下表所示。
▼建设空间与生态用地差异对比标识代码表
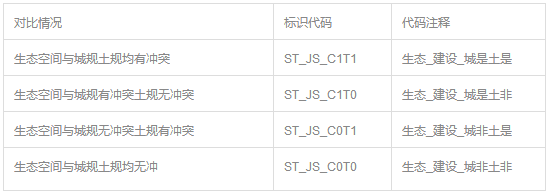
*注:此处的"是"表示建设用地与生态空间有冲突,"非"表示对于建设用地与生态空间无冲突
4.3 生态空间用地差异
根据《重庆市区县"多规合一"一张图编制技术指引》的表述,生态空间用地差异主要是对以下用地的重叠情况进行对比。
查找土规的林地、园地与林地保护与利用规划的林地的重叠情况,重点标识国家级公益林、I级、II级保护林地与土规林地的重叠。
查找城市规划、土地利用总体规划、水资源管控及水利设施布局规划的水域空间以及湿地的重叠。
查找土地利用总体规划的耕地、永久基本农田与其他生态要素的重叠情况,重点标识永久基本农田与国家级公益林、I级、II级保护林地的重叠。
根据以上对比要求,我们设计出生态空间用地差异对比情况一览表:
▼土地利用总体规划和林地保护与利用规划的林地对比代码表
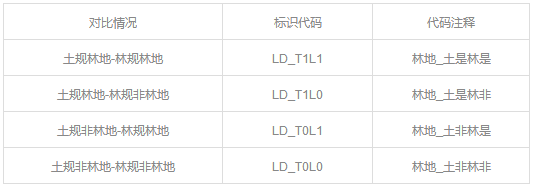
▼土地利用总体规划和林地保护与利用规划的园地对比代码表
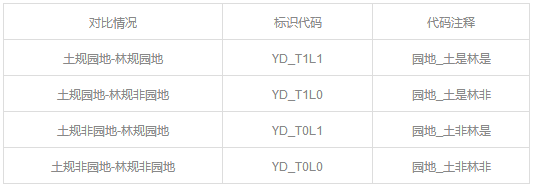
▼城乡总体规划和水资源管控及水利设施布局规划的水系对比代码表
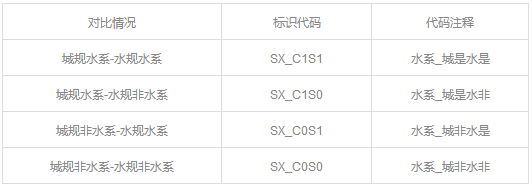
▼土地利用总体规划和水资源管控及水利设施布局规划的水系对比代码表
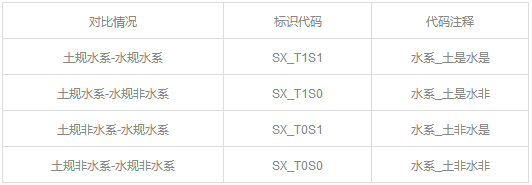
▼土地利用总体规划和永久基本农田图斑对比代码表
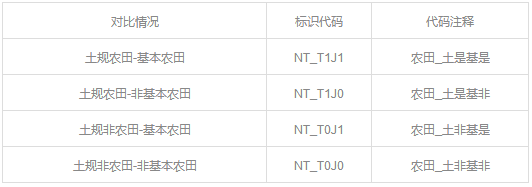
▼国家级公益林、I级、II级保护林地等林地空间与永久基本农田图斑对比代码表
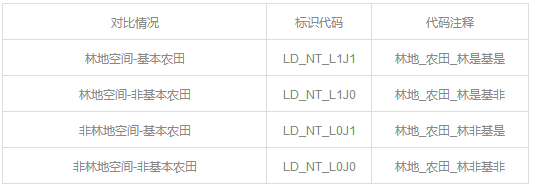
五、差异用地协调
差异用地协调主要是针对上述各类用地差异对比中存在不一致的用地要协调一致,保证不同规划相同地类的一致性,保证建设空间、生态空间和基本农田空间不冲突。
根据《重庆市区县"多规合一"一张图编制技术指引》,差异用地协调遵循如下原则:
1.优先保障生态空间
坚持生态优先,做到"应保尽保"。实事求是增补或调整生态管控范围。
2.建设用地协调一致
对"两规"差异建设用地,分类、逐块核实,并结合建设条件、用地权属以及用地性质,协调平衡利益关系进行处理,做到"两规""指标一致、空间一致、分类一致"。
3.急用先行重点保障
保障区县城市建设用地需求,十三五期间建设需求,城镇重大基础设施、公共服务设施、民生工程建设需求。
4.精细边界、有效利用
原则上以高精度为准修正差异用地边界。
5.1 建设用地差异协调
城规和土规的建设用地应通过差异协调做到空间边界范围、用地类别、用地规模及指标的一致性。
(1)空间边界协调一致
对于城规土规建设用地不一致的图斑应通过权属和用地类别确认后明确是否为建设用地,并确保与生态空间和基本农田图斑避让后统一为建设用地或非建设用地。
在用地确认过程中,城市、镇规划建设用地范围内原则上以城规为准,城市、镇规划建设用地范围外原则上以土规为准,具体根据各地块实际使用及规划情况确定。
(2)用地类别协调一致
城乡规划和土地利用总体规划用地分类标准差异导致对同一类用地有不同的表述方法,但彼此又有对应关系,因此我们应对两者进行对比,以保证同一用地在城规和土规中的表述一致性。
▼土地利用总体规划与城市用地分类对照表
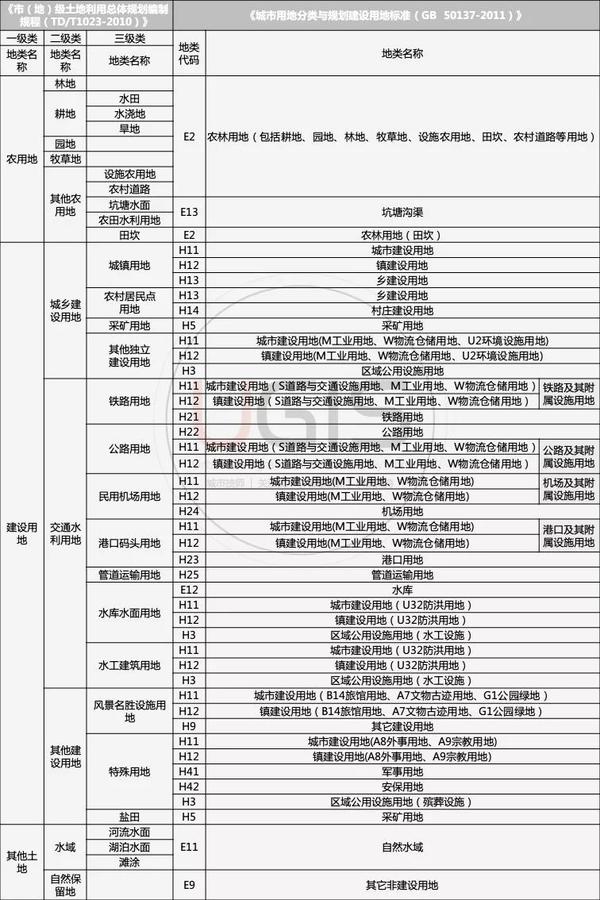
(3)用地规模及指标一致性
在保证建设用地边界及用地类别一致性的前提下,应保证两规协调合一后的建设用地规模分别符合城乡总体规划和土地利用总体规划的相应控制指标。包括城规城镇建设用地和发展备用地的总量与土规城镇用地、其他独立建设用地以及有条件建设区的总指标一致。
5.2 建设与生态空间差异协调
生态优先,应保尽保。建设空间用地与生态空间用地村庄冲突的时候,应优先保证生态空间,原则上建设空间对生态空间进行避让。
5.3 生态空间的差异用地协调
依法依规,从严管控。对不同生态空间重叠区域应根据相关管控要求,从严进行管控,原则上生态安全重要性低的应遵从重要性高的,管控力度小的应遵从力度大的。
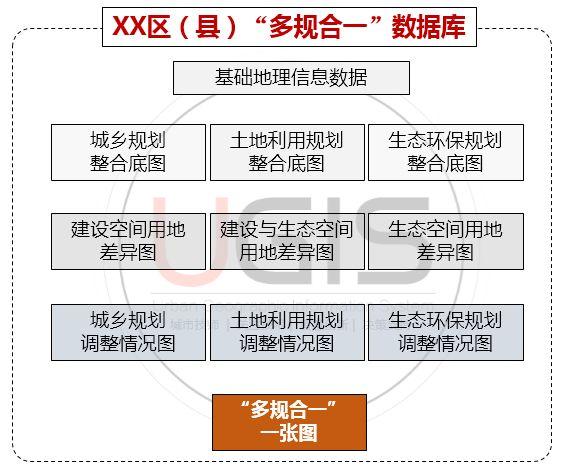
六、"多规合一"一张图成果
通过以上的基础资料搜集、各类规划整合、差异用地对比及协调,最后形成各区县"多规合一"一张图数据库成果,其中包括:基础地理信息数据、城乡规划整合底图、土地利用规划整合底图、生态环保规划整合底图、建设空间用地差异图、建设与生态空间用地差异图、生态空间用地差异图、城乡规划调整情况图、土地利用规划调整情况图、生态环保规划调整情况图、"多规合一"一张图。
后续预告
多规合一数据库的设计及数据入库操作
多规整合底图的制作 要点
多规用地差异对比及协调
敬请期待
(申明:本公众号提供的所有数据和资源仅作学习交流使用,严禁私自用作商业及非法活动,否则后果自负,本公众号不负连带责任。)
城市技师 | 关注技术 | 智慧创新 | 决策支持
我们关注城乡规划领域的GIS地理信息和时空大数据相关研究理论、前沿资讯、先进技法、优秀案例的共享、共创、共进、共赢。
来源:知乎 www.zhihu.com
作者:
柠檬 【知乎日报】千万用户的选择,做朋友圈里的新鲜事分享大牛。
点击下载
旋量中的左手旋量和右手旋量是相等的
,
相比于第一个分量
是一个小量
,
故有:
, 而
就是总角动量
的共同本征子空间的态矢量可以由
的共同本征矢量来作为基底,
所以原先的角量子数
不是好量子数,
,中的算符互相对易
这个子空间中将
算符的矩阵对角化即可得到合成的方法
分别对应于
的情形
,

即
起到了升降算符的作用
,所以
, 重新标度
并令
则方程可以化简为
,
,
,并重新标度
则方程可以变形为
其中,
为精细结构常数.