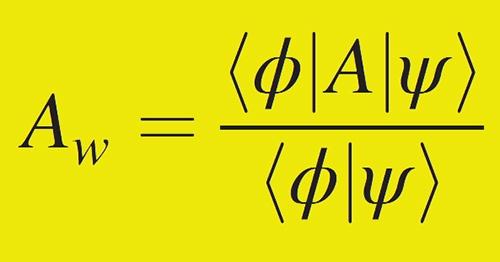
经典网文分享: 2. 小科普er~量子悖论：为什么物理学家着迷于杨氏的两个'缝'呢？说来话长，都是波粒二象性惹的祸！

第二章量子悖论：Three-boxes paradox(三抽屉量子悖论)和'which-way' paradox(杨氏双缝干涉实验)

------Yiming Pan (枫林白印)（原创，转载请注明出处）

如题，我是一个满脑子恶趣味的人，今天来介绍的是杨氏双缝干涉实验。虽然这两个'缝'已经被无数科学家和物理工作者折腾过，但是我仍然会尽可能从弱值理论重新梳理一下，让读者相信，搞研究也许还能发现一些未知的物理。在前面一章中，我介绍了弱值的理论形式以及它的哲学问题，不过并没有具体来讨论它的应用。你知道的，那种哲学上的辩论，每个人因角度不同，可以无止境地形而上地进行下去的。

我们还是干点物理学家该干的活儿 - 搭模型，搞计算！

接下来，我会介绍三个有趣的实验：一个是关于1/2自旋的Stern-Gerlach实验，另一个是three quantum boxes实验，和最后一个单电子双缝(double-slit)干涉实验。

他们的共同点是都是用弱值分析单量子态的诡异结果，至于双量子纠缠态的众多弱测量设计将会在下一章介绍。更复杂的三量子态或者多量子态的情况，我就没看到什么讨论过，你们也不会在这个专栏中看到它们。因此，我们基本上只是在用弱值分析一个量子态或者两个量子态的传播和测量行为。其实对我个人来说，多粒子或者无穷多粒子情况下弱值理论正是值得我们去发展研究的。

Aharonov第一篇弱值工作(1988)：自旋为1/2的电子, 会不会被测出自旋的大小超过100呢？

是的，有可能。考虑一个Stern-Gerlach实验设置，我们来计算它在z-方向投影的自旋分量大小，即 $\langle\sigma_z\rangle$ ，如图所示。

图：Stern-Gerlach实验装置来测量z方向电子自旋。摘自:Aharonov, Y., Albert, D. Z., & Vaidman, L. (1988) Physical review letters, 60(14), 1351.

按照弱测量的套路，我们预选择电子的初态(pre-selection)和后选择它的末态(post-selection)分别是，

$|i\rangle=\frac{1}{\sqrt{2}} \begin{pmatrix} \cos \alpha/2+\sin \alpha/2 \\ \cos \alpha/2-\sin \alpha/2 \end{pmatrix} ; \quad |f\rangle=\frac{1}{\sqrt{2}} \begin{pmatrix} 1 \\ 1 \end{pmatrix}$ （#1）

其中初态 $|i\rangle$ 的自旋方向在xz-平面内跟x轴的夹角为 $\alpha$ ,而末态 $|f\rangle$ 则是沿着x轴方向。对于自旋为1/2的电子系统，我们引入Pauli算子来表示xyz-方向的自旋分量的测量操作，即

$\sigma_x= \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix} ;\;\sigma_y= \begin{pmatrix} 0 & -i \\ i & 0 \end{pmatrix} ;\;\sigma_z= \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix}$

这三个2*2矩阵和单位矩阵满足一些有趣的性质，被称之为Clifford代数。我们刚刚定义了(#1)末态 $|f\rangle$ 不是沿着x轴方向嘛，因此你可以想象到如果用 $\sigma_x$ 作用上去的话，那么这个态将不会转动到其他角度上去，也就是 $|f\rangle$ 是 $\sigma_x$ 的本征态之一，即 $\sigma_x |f\rangle=|f\rangle$ 。[ref:Pauli matrices - Wikipedia]

PS: 因为是知乎文章，所以我就多说几句：太多人讨论量子力学，甚至是滥用量子力学中的概念，如何运用知识其实是个人的本事和自由，也不好指责什么。大家都知道，量子力学有很多哲学上的问题，但正因这一点常被不怀好意的人拿来误导读者和听众。因此我打算介绍两条标准，帮读者识别骗子的"量子诡计"：

Pauli矩阵：这是学量子力学的最低要求的代数知识，如果那人连Pauli矩阵都写不出来，别信他任何关于量子方面的诡辩；
谐振子模型：这是量子力学中最基本也是最普遍的'标准模型'了，如果他（她）写不出来谐振子的能量本征谱，这人量子力学怕是不及格的，也不能听信他的谎话。

言归正传，我们来看Pauli算子 $\sigma_z$ 的弱值是多少，即

$\langle \sigma_z\rangle_w=\frac{\langle f|\sigma_z |i\rangle}{\langle f| i\rangle}=\tan \alpha/2$

这个弱值便是可以从仪表中直接读出来的数字。当角度 $\alpha\rightarrow \pi$ ，这个 $\sigma_z$ 的弱值趋向无穷大。想想看，一个Pauli算子的本征值要么是+1要么是-1，怎么会在这个弱测量实验中数值大小超出100呢？即，超出可能的本征值范围100倍，怎么会这样呢？我一会儿来解释这个事儿，弱测量实验是有代价的。

Three-boxes paradox(三抽屉量子悖论)

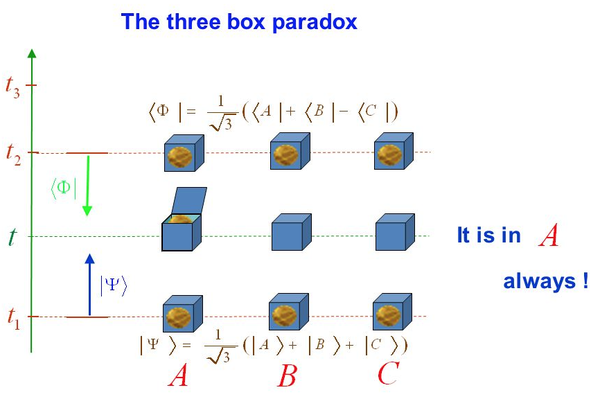
图：Three-boxes paradox(三抽屉量子悖论)，摘自Lev Vaidman, https://ift.tt/2uOw02H.

当然对于熟悉自旋1/2和Stern Gelarch实验的读者，建议去看AAV的第一篇弱值理论文章(88')，那是一篇充满物理思想的文章，易于从头学习弱值。这儿，我想用最短的篇幅把弱测量中反常现象展示出来，比如反常的代数关系和负概率问题，让读者陷入两难又被迫去抉择，而不会给更多解释。

我们再来看一个更简单的思想实验 - Three-boxes experiment(三抽屉量子悖论)：考虑一个粒子可以放在三个量子抽屉里面，比如我们在t_1时刻预选择一个叠加态:

$|i\rangle=\frac{1}{\sqrt{3}}(|1\rangle+|2\rangle+|3\rangle)$

然后我们再在t_2时刻(t_2>t_1)后选择一个叠加态：

$|f\rangle=\frac{1}{\sqrt{3}}(|1\rangle+|2\rangle-|3\rangle)$

这个末态跟初态满足一样的几率分布，唯一不同的是第三个抽屉(*3*)的符号相反，即翻转 $\pi$ 相位 $e^{i\pi}=-1$ 。那么在t1和t2时刻之间的某一时刻t (i.e., t_1<t<t_2)，我一不小心打开其中一个抽屉瞟一眼，能够看到这个粒子的几率是多少呢？为此，我们得先定义一下我们"一不小心"的操作过程所对应的算子表达，即

是的，这三个投影算子具有的性质是 $P_{1,2,3}^2=P_{1,2,3}\Rightarrow P_{1,2,3}=0 \text{ or }1$ ，即本征态是0或者1。因此，这三个算子满足我们对打开抽屉这一操作过程的描述，即打开抽屉看到了粒子即为1，而没看到则为0（注意：我们搞物理研究的，构造一个算子以及它所对应的物理操作是一件非常任性的事情，并不像大部分人以为得那么刻板缺乏想象力！）

如果我们一不小心打开第一个抽屉(*1*)偷看了一眼的话，那么这个粒子存在的几率是多少呢？

$\langle P_1\rangle_w=\frac{\langle f|P_1 |i\rangle}{\langle f| i\rangle}=1$

恭喜你，你看到它呢！它在第一个抽屉里面。

如果我们是打开了第二个抽屉(*2*)偷看了一眼的话，

$\langle P_2\rangle_w=\frac{\langle f|P_2 |i\rangle}{\langle f| i\rangle}=1$

恭喜你，你看到它呢！它在第二个抽屉里面。。。唉，等一下，它刚不是在第一抽屉里面吗？第二个抽屉里面应该没有粒子才对嘛。

它怎么会即在第一个抽屉里面，又在第二个抽屉里面呢？那么它是同时在两个抽屉里面吗？为此，我同时打开两个抽屉偷看一眼，即测量联合算子( $P_1*P_2$ )

$\langle P_1P_2\rangle_w=\frac{\langle f|P_1P_2 |i\rangle}{\langle f| i\rangle}=0$

还好，没看到。"吓死我了，我以为粒子会分裂成两个了呢！"

因为粒子在抽屉1和在抽屉2里面的情形是互斥事件，因此联合概率为零是可以理解的！但是为什么我打开第一个抽屉的时候，粒子就会出现在第一个抽屉；而打开第二个抽屉时它就又出现在第二个抽屉呢？这个怎么一回事儿啊！

根据上面的分析，我们得到弱值的一条"很没用"的性质：弱值不满足乘法结合律，即

$\langle P_1P_2\rangle_w\ne \langle P_1\rangle_w\langle P_2\rangle_w$

这个性质没啥意思也不讨人喜欢。我会在双量子纠缠态的弱测量分析中再来讨论它，因为它涉及到一个所谓'纠缠算子'的概念(对应于纠缠态)，投影算子 $P_1,P_2$ 并不相对独立。

再来看最后一种情况：如果我们一不小心打开第三个抽屉偷看了一眼的话，那么这个粒子存在的几率是多少呢？

$\langle P_3\rangle_w=\frac{\langle f|P_3 |i\rangle}{\langle f| i\rangle}=-1$

我们得到了一个无比尴尬而诡异的结果，即这个粒子在第三个抽屉中存在的几率不是0也不是1甚至也不是介于0到1之间，而是-1！

概率是-1，这什么鬼！！！

我必须要强调的是，这就是著名的"负概率问题"，它被很多人思考过或者定义过。[Ref:Mückenheim, et al.(1986) A review of extended probabilities. Physics Reports, 133(6), 337-401.]

在三抽屉量子悖论实验中，这个负概率的弱值，其实是记录了预选择和后选择在抽屉3量子态上存在的 $\pi$ 相位差。这个著名的负概率问题，也曾在大量的物理理论和物理系统中被注意到，比如像Bayesian估计，Winger准概率分布函数，Klein-Gordon方程等，这儿就不一一给参考文献了。

至于如何理解负概率问题，我个人是非常鸵鸟式的，即'假装没看见'。当然，还是有一部分人对于负概率问题给予自己的理解，大致分为两种：一种是认为这种出现负概率的理论是狗屎(bullshit)，不值得研究，否定其存在；而另一种是认为负概率其实是"反物质"或者"反事件"的正概率的一中异常现象，这是类比于Dirac预言正电子的思路。

更夸张地是，在弱测量中概率还可以是虚数的(complex)，比如我们后选择一个末态

$|f'\rangle=\frac{1}{\sqrt{3}}(i|1\rangle-|2\rangle-i|3\rangle)$

这时我们可以得到，

$\langle P_1\rangle_w=-i\\ \langle P_2\rangle_w=1\\ \langle P_3\rangle_w=i$

亲爱的读者，请帮我想想虚概率又是什么？注意："负概率问题"在弱值理论中是如此普遍的存在，因此常常被人诟病！

简单汇总一下，我们介绍了两个弱测量实验，看到了单量子态系统中弱值的三个性质：

算子的弱值，可以超出其本征值范围；
弱值不满足乘法结合律；
弱测量中的存在大量的"负(negative)概率，或者复(complex)概率"问题。

我是一个非常old-school型搞研究的。看到这么多弱值的诡异性质，为什么还会天真地相信像炼金术一样诡异的量子弱值理论呢？

说来好笑，是因为一部动漫《钢之炼金术师》拯救了我对弱值理论的信心。

炼金术第一原则：等价交换！同样地，弱值理论中的诡异行为的发生并不是没有代价的，即，越是违反常识的结果，所需要付出的代价越大！

这个代价函数(price)就是存在于预选择和后选择的成功几率中，即

$P=|\langle f|i \rangle|^2$

注意这个代价函数P并不是ABL定理，它说的是能够完成一次弱测量的可能性：如果我们重复N次实验，那么大概只有P*N次实验是有效的弱测量，而剩下的(1-P)*N就要被无情地丢掉。举例来说，在Stern-Gerlach实验中 $\langle \sigma_z\rangle_w=\tan \alpha/2$ ，那么它的代价函数就是 $P=\cos^2 \alpha/2$ 。也就是说，如果 $\langle \sigma_z\rangle_w=100$ ，那么 $P\approx1/10000$ ，即你做了10000次后选择的测量实验，而只有一次的测量数据是被记录下来的，而剩下的9999次实验的后选择是不成功的因此测量数据不能用，因为后选择并没有把系统投影到末态上去。而要获得诡异的弱值的预选择和后选择双矢量子态系统(TSVF)，实在是太难筛选出来了，因为初态和末态几乎正交( i.e., $P\approx 0$ )。所以说，弱值虽然很诡异，像炼金术一样，但它是有代价的。越诡异的弱值，它的弱测量实验代价越高！

'which-way' double-slit paradox(电子杨氏双缝干涉实验)：为什么物理学家这么喜欢研究它呢？

虽然标题党是一种恶趣味，但是我确实会简单解释一下：为什么物理学家这么喜欢研究杨氏双缝实验(Young's double slit experiment)?

不管你是一个科研工作者，还是一个物理爱好者，或者被物理考试烦得不行的学生，不妨想想，为啥搞物理的天天研究这两个"缝"呢？道理很简单，这么多年来，我们发现这两个"缝"里面有真理！就像男人迷恋女人一样，物理学家迷恋着双缝实验，并孜孜不倦地专研它！

这个真理，就是要回答：我们的世界的基本元素是波动组成的，还是粒子组成的？

从17世纪下半叶开始，光是微粒的还是波动的就被同时建立起来了。其中，微粒说的代表人物就是牛顿(Isaac Newton, 1642-1726/27)，而同时代波动学说的代表是另一个大科学家惠更斯(Christiaan Huygens, 1629-1695)。光的微粒学说几乎主导了整个17世纪末到19世纪初100多年的物理学史。

直到1802-1807年期间杨氏(Thomas Young)陆续报道了关于光的双缝干涉实验，才慢慢坚定了关于惠更斯波动学说的研究，然后来到1818年法国Fresnel的波动理论以及Poisson的Poisson光斑的理论和实验的建立和验证，光的波动学说就被广泛接受了。19世纪下半叶，赫兹(Heinrich Hertz)进一步实验证实了Maxwell的预言，即光是一种电磁波，并同时给出来光电效应的实验结果。光的波动学说大获全胜，但是解释不了光电效应！

一直无法用波动光学来解释的光电效应，直到1905年被爱因斯坦(Albert Einstein)利用光量子的"微粒"概念成功解释了。到后来激光的发明，以及量子光源的实现，纠缠光子对的实现等等，这些后来的历史发展太迅速，就不细说了。有趣的是，在我们对光的波粒二象性认识过程中，我们总是在不断变着花样地重复着杨氏双缝干涉实验。

我们发现光是电磁波，去做杨氏双缝干涉实验；
我们解释了光电效应，去做杨氏双缝干涉实验；
我们发现了激光光源，去做杨氏双缝干涉实验；
我们实现了纠缠光子对，去做杨氏双缝干涉实验；

我们在历史上的每一次的光源更新或者测量技术提高，第一件事情还是去检验一下杨氏双缝干涉实验！这个研究光的波粒二象性的研究模式，同时地，被研究电子的物质波特性照搬下去了。在1924年，德布罗意(de Broglie )提出电子也是一种波之后，我们猜测电子是一种波，又去做关于电子的杨氏双缝干涉实验！

简单来说：有波，就要有缝，而且必须是"杨氏的双缝"！

波粒二象性的一个双缝仿真视频值得推荐一下，可以去Wikepedia词条中寻找：参看Wave-particle duality. 波粒二象性(wave-particle duality, wave-particle dilemma, duality paradoxes)本质上认为物质和光其实都是波的，而且是量子化的波，跟经典的粒子没有太大的关系，这儿的粒子性主要是指的它是量子化。而波粒二象性是用一种'悖论"式来展示量子波，和经典粒子-经典波之间的异同。

杨氏双缝干涉实验[refs: Young's interference experiment; Double-slit experiment]可以用来理解，粒子性，波动性以及波粒二象性，也可以用来描述量子力学中的测量坍缩问题以及量子纠缠问题比如量子擦除实验等，也可以用来理解比如x,p的测量不对易问题，Fourier变换过程以及Heisenberg的不确定性原理，即 $\Delta x \Delta p\geq \hbar/2$ 等。

细数物理学中，能跟杨氏双缝实验叫上板的，除了迈克耳孙干涉实验（Michelson-Morley experiment及其拓展，比如引力波的测量装置，量子延迟实验等）还真不多。

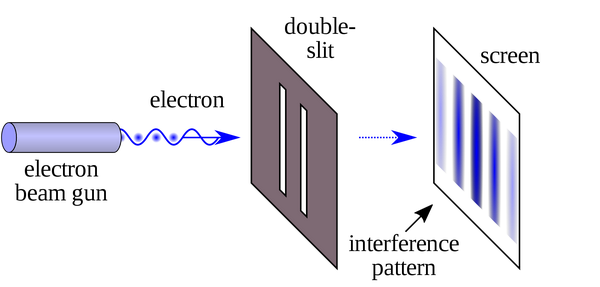
最后，我们来点一下题：能不能用弱测量的办法做电子的双缝实验，同时获得屏幕上的干涉条纹以及确定电子通过哪一个缝？这便是著名的-which-way(which-path) paradox！

图:电子杨氏双缝实验中的"which-way"量子悖论，图摘自于Aharonov, quantum paradoxes.

说实在的，我并没有太明确的答案，但是弱测量版本双缝实验是可能的，参看Wikipedia：Double-slit experiment中的"which-way experiment'以及Svensson的评论"Pedagogical Review of Quantum Measurement Theory with an Emphasis on Weak Measurements". Quanta. 2 (1): 18–49.

这个which-way paradox是一个单量子态传播和测量问题，也是再一次让我变成鸵鸟的问题！

我估计，只有亲自做实验的人，搞出一个简单却很天才式的实验方案来，把它突破或者证伪了，就像杨氏双缝干涉实验对于光的研究来说。而我们搞理论的，说实在的，已经尽力了！

(第一稿：30-March-2018)

来源：知乎 www.zhihu.com
作者：Yiming Pan

【知乎日报】千万用户的选择，做朋友圈里的新鲜事分享大牛。点击下载

经典网文分享

2. 小科普er~量子悖论：为什么物理学家着迷于杨氏的两个'缝'呢？说来话长，都是波粒二象性惹的祸！

没有评论:

发表评论