(哇,居然有这么多人关注,多谢大家的厚爱!)
(本文只是简要回顾经典的波函数方法,为了不让之后的文章显得太过突兀,不涉及技术细节)
量子化学,顾名思义,是应用量子力学的基本原理和方法研究化学问题的一门基础科学(摘自百度百科)。 其最基本的物理便是量子力学.
在 Born-Oppenheimer approximation 近似的框架下,量子化学的基本任务是(近似)求解如下电子的 Schrodinger 方程:
(上式中 A 代表原子核,原子核位置固定)
1. 波函数
体系的波函数当然不是任意的函数,除了满足上述方程外, 量子力学要求电子波函数满足反对称性 . 同时由于处理的是非相对论情形,哈密顿量不含自旋, ,以及对于体系的对称操作 P,有
,体系的波函数应是
四个算符的共同本征态. 总结起来便是(至少)要满足如下三个条件:
(1) 波函数是反对称的;
(2) 波函数是 的共同本征态(spin-adapted);(注:专栏接下来的几篇文章便是围绕如何构造 spin-adapted 的波函数展开,同时探讨如何在这些波函数上高效计算矩阵元)
(3) 波函数是分子点群不可约表示的基(symmetry-adapted) .
2. 量子化学计算方法
基于以上考虑,几十年来发展了一系列量子化学计算方法,其中最经典的便是 Hartree-Fock 方法. 其是以单个行列式为基做变分求极小值得到的方法. 具体如何推导和计算的有时间再聊,简单说说为什么要用行列式.
因为波函数是反对称的,最简单的想法便是取行列式。其实,从置换群的知识可知 (波函数是反对称的,用群论的语言便是,其是置换群反对称基 ) 将一个不对称的函数对称化成反对称的函数,得到的结果是若干个行列式的线性组合. Hartree Fock 方法便是取最简单的情形,就是假定体系波函数可以用一个行列式近似
(其中各个 是自旋轨道可以写成空间部分和自旋部分的乘积例如
)
在此基础上做变分.
但 Hartree-Fock 方法并不能处理所有的问题,比如 氢分子的解离曲线都算不对.
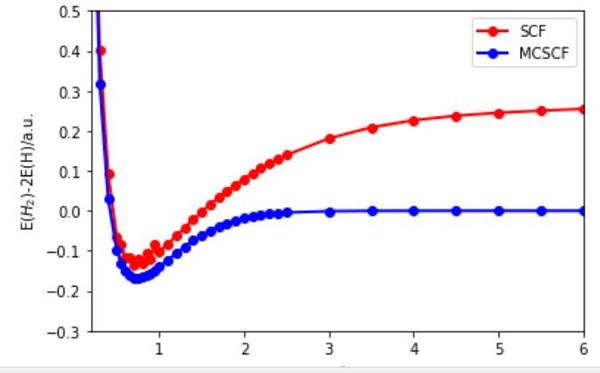
(软件:Molcas, 基组:6-31G*)
当两个原子距离无穷大的时候, 氢分子解离 ,但 Hartree Fock 方法并没有给出这样的结果, 当
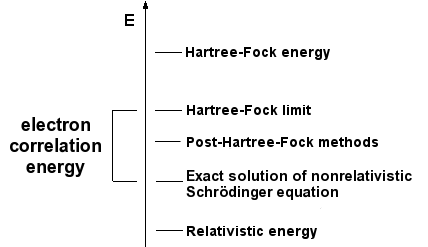
时,Hartree Fock 方法就失效了,体系只用一个行列式描述这个近似就不是很好的近似. (而且 Hartree Fock 方法没法求解体系的激发态) (其实这个例子也说明了电子相关能
有时候是没有物理意义的.)
于是就要想办法去处理这个问题,最简单粗暴的想法,就是不用一个行列式,用多个行列式不就完了. 从这个思路往下走便衍生出诸多 多组态的波函数方法. 现在假定 我们已经使用 HF 方法得到一组分子轨道 ,能量依次上升,其乘上自旋函数
便是自旋轨道.
(1)组态相互作用(Configuration Interaction)
组态相互作用方法的思路很简单,分子轨道取 HF 得到的轨道,然后电子可以在这些轨道中任意的占据.
比如对于氢分子的基态(单重态),考虑两个轨道. HF 假定的波函数可由行列式 (
代表
电子) 近似 .
而 CI 方法 ,电子可在各轨道间任意排布,每一种排布对于结果都有贡献。比如 氢分子基态可写成 .也就是把等式右边的四个行列式(每个行列式可形象地理解为一个 Configuration )作为基组, 结合线性变分法,将
在这个基组下的矩阵对角化,求解出相应的本征值,和系数.
一般地, 如果有 n 个分子轨道 ,N 个电子 则有 个可能的行列式, 哈密顿算符在这个空间下的矩阵,对于大的体系将会非常巨大. 虽然理论上,如果计算用的基组是完备的,该方法可以得到原方程的精确解,但实际上由于计算能力和储存的限制,对于大体系该方法无法用于实际计算. (注意 CI 方法不优化分子轨道)
(2)MCSCF
多参考态自洽场方法,与 CI 方法不同的是其给定一组行列式,每步迭代同时优化行列式间的组合系数和分子轨道.
比如即使 有 个分子轨道,我仍假定氢分子的基态可以写成
之后优化系数和相应的轨道即可.(但这种方法的程序实现比 CI 要难得多)
(3)CASSCF
其也是一种多组态的方法,只不过选取 Configuration(也就是行列式) 的方法更自然,当然也需要一定的化学知识. 比如对于苯分子, 有机化学告诉我们其化学性质主要由 轨道决定,那么就选取 6 个
电子,其排布在 3 个占据的
轨道(这里的轨道不是自旋轨道,一个轨道上至多占据两个电子),以及 3 个能量最低的
轨道 .而其他电子仍占据在
轨道.这样就构成了 Complete Active Space(CAS),其维数是
维. 之后同 MCSCF 一样进行组合系数和分子轨道的优化即可.
多组态的均可以用于研究分子激发态,一下是我用 MCSCF 方法得到的 氢分子的势能曲线,其中 MCSCF-1,3 是单重态, 2,4 是三重态.
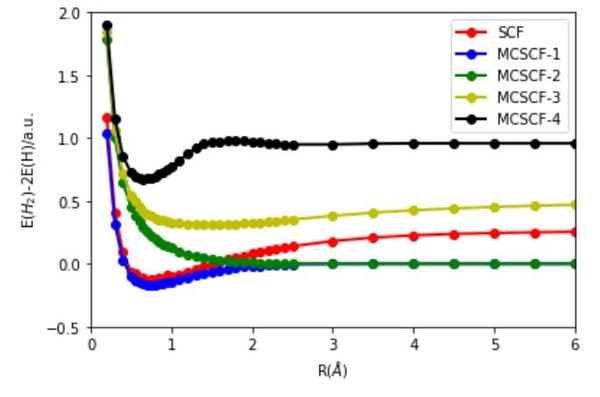
(好多细节没有详细展开,感觉挖了好多坑,还请各位见谅!)
【参考文献】
- Attila Szabo,Neil S. Ostlund, Modern Quantum Chemistry.
来源:知乎 www.zhihu.com
作者:追寻炼金师的脚步
【知乎日报】千万用户的选择,做朋友圈里的新鲜事分享大牛。 点击下载
没有评论:
发表评论