经典网文分享: 自旋液体 in a nutshell（二）

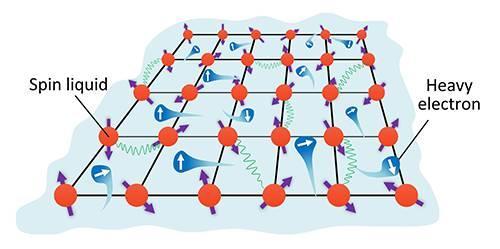
上篇介绍了构造自旋模型平均场的一种方法——schwinger-fermion（近来都叫Abrikosov fermionic method）方案。

第二篇进一步介绍一下其他两种的slave-particle方案。

第三篇回顾一下PSG（projected symmetry group）方法和附带的一些东西（flux, 平均场拟设，unbiased structure & rotation-gauge relation）。

我们知道对于heisenberg model用schwinger-fermion方式进行slave-particle手续后，变成了一个理论 that is described by $f_{\uparrow}^{(\dagger)},f_{\downarrow}^{(\dagger)}$ 描述的费米子和一个 $SU(2)$ gauge structure，平均场附近的涨落可以表述为这个gauge structure内部的变换。因此，我们在平均场的框架下可以看到自旋液体流动的"形状"。

事实上，对自旋算符的slave-particle方法不止一种，在这里，我再另外简单介绍两种：bosonic method和Majorana fractionalization method。

先回顾我们的起点——海森堡反铁磁模型：

$\bm{H_{AH}}=\sum_{<ij>}J\bm{S_{i}}\cdot \bm{S_{j}}， J> 0$

一：bosonic method：

跟Abrikosov fermionic method类似，还是对自旋 $\bm{S}$ 作一下分解：

$S^{a}=\frac{1}{2}b^{\dagger}_{\alpha}\sigma_{\alpha\beta}^{a}b_{\beta}，a=x,y,z，\alpha ,\beta=\uparrow ,\downarrow$

此处默认同指标求和规则， $b^{(\dagger)}$ 是玻色子算符，因此它跟Abrikosov fermionic method不同在于它们满足对易关系：

$[b^{\dagger}_{i\alpha},b_{j\beta}]=\delta_{ij}\delta_{\alpha\beta}$

而前者则满足反对改称关系。

由于自旋液体态不破坏旋转对称（上一篇中对 $\bm{F}= \left(\begin{array}{cccc} f_{\uparrow} & f_{\downarrow}^{\dagger} \\ f_{\downarrow} & f_{\uparrow}^{\dagger} \\ \end{array}\right)$ 的 $SU(2)$ 左作用为spin rotation），我们希望得到一些不破坏自旋旋转对称的算符，以算符的平均值作为平均场的参数，简单起见，取算符的二次项：

$A_{ij}=(b_{i\uparrow}b_{j\downarrow}-b_{i\downarrow}b_{j\uparrow})$ $B_{ij}=(b_{i\uparrow}b_{j\uparrow}^{\dagger}+b_{i\downarrow}b_{j\downarrow}^{\dagger})$

还有它们的共轭。

这个方法剩余的下篇PSG时再说。

二：Majorana fractionalization method：

对 $\bm{F}= \left(\begin{array}{cccc} f_{\uparrow} & f_{\downarrow}^{\dagger} \\ f_{\downarrow} & f_{\uparrow}^{\dagger} \\ \end{array}\right)$ 作以下分解：

$\bm{F}=\frac{1}{2}(is+\bm{\sigma} \cdot \bm{t})$

$s$ 是Majorna单态， $\bm{t}=\left(\begin{array}{cccc} t_{1} \\ t_{2} \\ t_{3}\end{array}\right) \$ 是Majorana三重态，

满足majorana的反对易关系：

$\left\{ s_{i},s_{j} \right\}=2\delta_{ij} ，\left\{ t_{\alpha i},t_{\beta j} \right\}=2\delta_{ij}\delta_{\alpha \beta}， \left\{ s_{i},t_{\alpha j} \right\}=0$

自旋算符：

$\bm{S}=\left(\begin{array}{cccc} st_{1} \\ st_{2} \\ st_{3}\end{array}\right) \$

这个slave-Majoranon方法有什么意义呢？由上篇知道，对 $\bm{F}= \left(\begin{array}{cccc} f_{\uparrow} & f_{\downarrow}^{\dagger} \\ f_{\downarrow} & f_{\uparrow}^{\dagger} \\ \end{array}\right)$ 左边和右边乘以一个 $SU(2)$ 矩阵的意义是不同的： $\bm{FU}$ 直接是规范变换， $\bm{UF}$ 诱导了 $SO(3)$ 自旋旋转。我们知道自旋液体态都存在这两种对称性。然而 $\bm{FU}$ 和 $\bm{UF}$ 显然不是相互独立的，两者存在unbiased structure，但无论如何，一般的自旋液体系统一定对于以下这个操作是对称的：

$\bm{F}\rightarrow\bm{UFU^{\dagger}}$

这个变换只包含一部分的自旋变换，和一部分规范变换（事实上去除了相位冗余，见下篇）。既然如此，我们可以考虑一个特殊的把以上操作当成自旋旋转变换并为之对称的自旋液体态（partial (projected) spin rotation symmetric QSL，见下篇）。在这个限制下，我们可以很容易很自然地从Majorana fractionalization method得到有效平均场理论，考虑对 $\bm{F}\rightarrow\bm{UFU^{\dagger}}$ 对称（可以自己验证）最一般的二次平均场哈密顿：

$H_{0}=\sum_{<ij>}i\chi_{ij}Tr(F_{i}F_{j}^{\dagger})+i\chi_{ij}'Tr(\sigma^{\alpha}F_{i}\sigma^{\alpha}F_{j}^{\dagger})$

其中系数 $\chi_{ij},\chi_{ij}'$ 是用 $\bm{F}$ 构造的平均场参量， $\sigma^{\alpha}$ 是泡利矩阵任意分量，我们再用slave Majoranon来表达：

$H_{0}=\sum_{<ij>}i\chi_{ij}^{s}s_{i}s_{j}+i\chi_{ij}^{t}\bm{t_{i}}\cdot \bm{t_{j}}$

其中 $\chi_{ij}^{s}=\frac{1}{2}\chi_{ij}+\frac{3}{2}\chi_{ij}'，\chi_{ij}^{t}=\frac{1}{2}\chi_{ij}-\frac{1}{2}\chi_{ij}'$ ，意不意外，惊不惊喜。原来我们丢掉一部分自旋旋转对称和丢掉一部分规范对称（丢掉的是给相互带来的相位冗余，见下篇）并重新组合成一个新的自旋旋转操作（projected spin rotation，见下篇）可以得到由类Majoranon的准粒子描述的有效理论，系统的gauge structure事实上破缺为 $\mathbb{z}_{2}$ （原因可从unbiased structure清楚看到，见下篇）。

来源：知乎 www.zhihu.com
作者：潇湘

【知乎日报】千万用户的选择，做朋友圈里的新鲜事分享大牛。点击下载

经典网文分享

自旋液体 in a nutshell（二）

一：bosonic method：

二：Majorana fractionalization method：

没有评论:

发表评论