经典网文分享: 实分析Ⅱ|笔记整理（3）—

大家好！

这一部分选自讲师花了两节课（实际上可能还拖了两节课的堂）讲的第一章的相关习题。它们多半都有一定的难度，很多的步骤都不是"顺其自然"可以想到的，因此可把这一节笔记内的证明思想一样作为积累为以后运用。

注意：这一节的习题主要会使用分析法来叙述，因此不能直接使用在试题或者教科书中。

提供之前的笔记：

我们开始本节的内容。本节是复习章节。

首先是一些集合语言的翻译题。

Problem 1:
试用 $\{x: f_j(x) \ge \frac1k\}$ 表示 $\{x: \overline{\lim_{j \to \infty} }f_j(x) >0 \}$

常规题，从左到右剖析每一个运算的集合意义。

首先我们在第一节介绍了 $\{x: \overline{\lim_{j \to \infty} }f_j(x) >0 \} = \bigcup_{k=1}^{\infty}\{x: \overline{\lim_{j \to \infty}} f_j(x) \ge \frac1k\}$ ，之后要注意函数上极限的定义（数分一中有），就是对一个函数列的上确界取极限，具体一些就是 $\bigcup_{k=1}^{\infty}\{x: \lim _{N \to \infty} \sup _{j \ge N} f_j(x) \ge \frac1k\}$ 。进一步想，如果 $N \to \infty$ 时，它的上确界列依然是 $\ge \frac1k$ 的，那么我在比较小的时候，这个上确界列也依然是满足这个条件的（在小的时候，要取上确界的函数值对象其实变多了，那么上确界的值自然不会减），而另一方面，如果对于每一个都满足这个不等式，那取极限自然也满足条件。根据这个思路我们可以得到它为 $\bigcup_{k=1}^{\infty}\bigcap_{n=1}^{\infty} \{x: \sup _ {j \ge N} f_j(x) \ge \frac1k\}$ 。接下来，如果存在 $j_0 \ge N$ ，使得这个函数的值是 $\ge \frac1k$ 的，那么自然对这个函数列取上确界也是满足条件的。所以进一步可以得到它为 $\bigcup_{k=1}^{\infty} \bigcap_{N=1}^{\infty} \bigcup_{j=N}^{\infty}\{x: f_j(x) \ge \frac1k\}$ 。这就已经完成了我们的构造。

Problem 2:
设 $\lim_{n \to \infty} f_n(x) = \chi _{[a,b] \setminus E}(x),x \in [a,b]$ ，令 $E_n = \{x \in [a,b] \mid f_n(x) \ge \frac12\}$ ，求 $\lim _{n \to \infty}E_n$

这个题的思路也是非同寻常的。首先我们不难猜得答案是 $[a,b] \setminus E$ ，所以要证明集合列的极限是这个答案，就需要考虑一个下极限和一个上极限。我们在第一节说过，一个集合列的上极限是比一个集合列的下极限要"不小"的。所以如果我们说明了这个集合它包含于一个集合列的下极限，却又包含了同样这个集合列的上极限，那么就足够证明结论了。

我们先证明 $[a,b] \setminus E \subset \underline{\lim}\limits_{n \to \infty} E_n$ 。取任意的 $x \in [a,b] \setminus E$ ，那么 $\lim _{n \to \infty} f_n(x)=1$ ，那么根据极限的定义，自然就说明，对于任意的 $\epsilon \in (0,\frac12)$ ，存在一个 $N \in \mathbb{N}^*$ ，使得 $f_n(x) > 1-\epsilon > \frac12 , n \ge N$ 。这就说明了 $x \in E_n,n \ge N$ ，也就是说，我们论证了存在一个满足对于任意的 $n \ge N$ 成立上面的条件，根据集合语言即可知 $x \in \bigcup_{N=1}^{\infty} \bigcap_{n =N}^{\infty}E_n$ 。这就是集合列下极限的定义。

下面，我们再证明 $\overline{\lim _{n \to \infty}}E_n \subset [a,b] \setminus E$ 即可。这里我们考虑对集合取一个补集考虑，意思就是说，只要证明不在右边的集合的元素一定也不在左边集合即可。那么如果 $x \not \in [a,b] \setminus E$ 。这就说明 $x \in E$ ，并且 $\lim_{n \to \infty}f_n(x) =0$ ，那么对于任意的 $\epsilon \in (0,\frac12)$ ，存在，使得 $n \ge N$ 时有 $f(x) < \epsilon <\frac12$ ，这就说明了 $x \not \in E_n$ 。那么自然不可能有 $x \not \in \bigcap_{N=1}^{\infty}\bigcup_{n=N}^{\infty}E_n$ （因为 $x \not \in \bigcup_{n=N}^{\infty}E_n$ ）。也就是它不在集合的上极限中，这就证明了结论。

Problem 3:
$\overline{\lim_{k \to \infty}}\chi_{E_k}(x) = \chi_{\overline{\lim\limits_{k \to \infty}E_k}}(x)$

这个命题是想说两个函数值是恒等的。注意到特征函数只有可能取到0或1，所以分别讨论两种情况自然就可以了。

假设 $\chi_{\overline{\lim\limits_{k \to \infty}E_k}}(x)=1$ ，这就说明 $x \in \bigcap_{N=1}^{\infty}\bigcup_{k=N}^{\infty}E_k$ ，翻译一下就是说，对于任意的 $N \in \mathbb{N^*},\exists k \ge N, s.t. ~x \in E_k$ 。现在我们再看看另一边，注意到函数值的上极限就是 $\lim \sup$ 的意思。那么把我们得到的解释语言翻译为特征函数，就是说，对于任意的 $N \in \mathbb{N^*}$ ， $\sup_{k \ge N}\chi_{E_k}(x)=1$ 。那么由于 $\overline{\lim _{k \to \infty}}\chi_{E_k}(x)=\lim_{N \to \infty}\sup _{k \ge N}\chi_{E_k}(x) =1$ ，所以自然就说明了结论。

假设 $\chi_{\overline{\lim\limits_{k \to \infty}E_k}}(x)=0$ ，那就是 $x \not \in \bigcap_{N=1}^{\infty}\bigcup_{k=N}^{\infty}E_k$ 。把上面的解释语言取反，就是说 $\exists N \in \mathbb{N^*} ~ s.t. ~ x \not \in \bigcup_{k=N}^{\infty}E_k$ 。那么自然对于任意的 $k \ge N, \sup_{k \ge N} \chi_{E_k}(x)=0$ ，这就说明了 $\overline{\lim _{k \to \infty}}\chi_{E_k}(x)=\lim_{N \to \infty}\sup _{k \ge N}\chi_{E_k}(x) =0$ ，也就得到了结论成立。

下面是关于集合是否可数的一些题目。

Problem 4:
设 $E \subset (0,1)$ 是无限集。若从中任意选取不同的数所组成的无穷正项级数总收敛，试证明可数。

首先因为 $E \subset (0,1)$ ，所以如果我们设 $E_n=\{x \in E : \frac1{n+1} \le x < \frac1n\}$ ，那么 $E = \bigcup_{n=1}^{\infty}E_n$ 。然后注意到每一个 E_n 内的元素都是有限个的即可（这是因为如果有一个集合 $E_{n_0}$ 它是无限集，那么取里面的元素就有 $\sum_{n=1}^{\infty}x_n \ge \sum_{n=1}^{\infty}\frac1{n_0}$ 发散），有限个是可数个，可数个可数集合并一下自然还是可数的，这就证明了结论。

对一个集合做"可数的拆分"是一个很重要的证明集合可数的方式。

Problem 5:
设是定义在上的实值函数，且存在常数使得对中任意有限个数 $x_1,x_2,\cdots,x_n$ 有 $|f(x_1)+f(x_2)+\cdots+f(x_n)| \le M$ 。试证明 $E=\{x \in [0,1] : f(x) \ne 0\}$ 是可数集。

事实上，设 $E_n=\{x \in [0,1]: n < |f(x)| \le n+1\}$ , $F_n=\{x \in [0,1] : \frac1{n+1} < |f(x)| \le \frac1n\}$ ，那么 $E=\bigcup_{n=1}^{\infty}(E_n \cup F_n)$ 。同样的思路，现在只需要说明，对于每一个固定的， $E_n \cup F_n$ 都是有限集即可。不妨假设存在 $F_{n_0}$ 是一个无限集，那么根据 $\sum_{k=1}^{M(n_0+1)}f(x_k) > M$ 即可推出矛盾，所以它每一个都是有限集，同理对 E_n 。所以 $E_n \cup F_n$ 每一个都是有限集。可数个并自然是可数集，结论证完。

Problem 6:
设是定义在 $\mathbb{R}$ 上的实值函数。若对于任意的 $x_0 \in \mathbb{R}$ ，都存在 $\delta>0$ ，使得 $|x-x_0| <\delta$ 时， $f(x) \ge f(x_0)$ ，证明 $E=\{y:y=f(x)\}$ 是可数集。

简单分析一下题目，意思就是说，对于任意的 $y \in E$ ，都 $\exists x \in \mathbb{R},~ s.t. ~ f(x)=y$ 。也就是说存在 $\delta_x>0$ ，使得 $\forall x' \in (x-\delta_x,x+\delta_x),f(x') \ge f(x)$ 。那么如何证明可数呢？这里的思路是，构造一个函数定义域内点到函数值的一一映射。

那么因为定义域需要构造成可数的。所以需要用有理数集做一些处理。取 $r_x \in (x-\delta_x,x) \cap \mathbb{Q},R_x \in (x,x+\delta_x) \cap \mathbb{Q}$ 。这样就有 $x \in I_y =(r_x,R_x) \subset (x-\delta_x,x+\delta_x)$ 。

考虑构造映射 $f:E \to \{I_y\}_{y \in E}$ ，那么根据映射的定义，满射是显然的。下面考虑证明它是一个单射。若对于两个元素 $y,y' \in E$ ，有 $I_y \in (r_x,R_x) =(r_{x'},R_{x'})=I_{y'}$ ，那么就有 $x \in (r_x,R_x) \subset (x'-\delta_{x'},x'+\delta_{x'})$ 。这样的话， $y=f(x) \ge f(x') =y'$ （注意一下我们证明开始部分的中间结论）。而证明 $y' \ge y$ 是同理的。也就是说是一个单射。

现在构造出了一一映射，又因为 $\{I_y\}_{y \in E}$ 是有理数的子集，那自然是可数集。结论证完。

Problem 7:
不存在 $\mathbb{R}$ 上的连续函数，其在无理数集 $\mathbb{R} \setminus \mathbb{Q}$ 上是一一映射，而在 $\mathbb{Q}$ 上不是一一映射。

我们假设存在这样的函数，那么自然存在 $a_0,b_0 \in \mathbb{Q}$ ，使得 f(a_0)=f(b_0)=y_0 。令 $E=\{x \in [a_0,b_0]:f(x)=y_0\}$ ，下面的证明重点自然围绕展开。

首先先证明 $\bar E \subsetneq[a_0,b_0]$ 。否则的话，就说明它在内是稠密的，也就是说任意的一个区间都会存在一个点它的函数值是 y_0 。这样的话，利用极限语言可知，对于任意的 $x_1,x_2 \in [a_0,b_0] \setminus \mathbb{Q}$ （既然你要推矛盾，自然要考虑无理数的方向），使得 $x_{k_1} \to x_1,x_{k_2} \to x_2,k \to \infty$ ，其中 $\{x_{k_1}\} \subset E,\{x_{k_2}\} \subset E$ 。由于函数是连续函数，所以可以考虑极限，因此这样的话可以得到 f(x_1)=f(x_2)=y_0 ，这就矛盾了（因为无理数上是一一映射）。

既然这个集合不稠密，那么自然存在 $x_0 \in [a,b] \setminus \bar E$ 与 $\delta_0 >0$ ，使得 $(x_0-\delta_0,x_0+\delta_0) \cap \bar E =\emptyset$ 。因为 $\delta_0$ 是可以任意小的，所以不妨设 $(x_0-\delta_0,x_0+\delta_0) \subset [a_0,b_0]$ 。

现在我们有了一个集合，它内的所有的元素的函数值都不是 y_0 ，那么考虑左右的函数值是 y_0 的相关点，看看是否有更好的结论。设 $a_1=\sup\{x \in [a_0,x_0-\delta_0],f(x)=y_0\}$ , $b_1=\inf\{x \in [x_0+\delta_0,b_0],f(x)=y_0\}$ 。这就说明 f(a_1)=f(b_1)=y_0 ，且对任意的 $x \in (a_1,b_1),f(x) \ne y_0$ 。又因为函数连续，所以要不函数值一直都大于 y_0 ，要不反过来。不妨设是前一种情况，那么存在 $\xi \in [a_1,b_1]$ ，这个点为函数的最大值点。又 $f([a,\xi] \setminus \mathbb{Q}) \subset f([\xi,b_1] \cap \mathbb{Q})$ ，而左边是一个不可数集，右边却可数，这就矛盾了。

重新理一下思路就是，你需要找到一个函数来说明反例，这需要利用区间的不可数性。为了让这样的区间存在，我们必须要说明它不稠密。下面这张图可以说明最后的解释的本质。

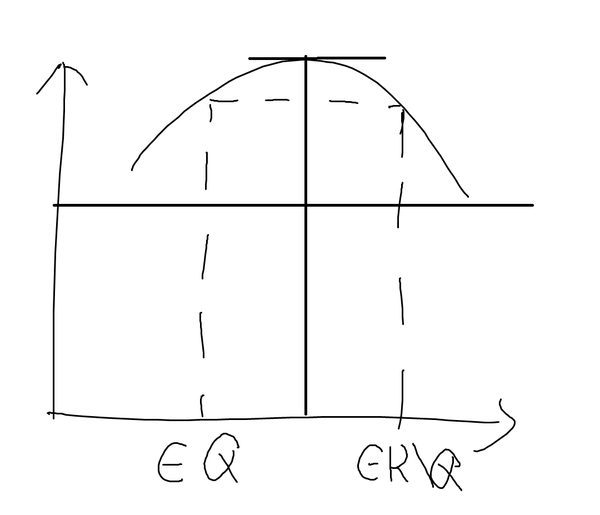
对于每一个具体的区间左边的元素，如果它是有理数，那么与之对应的右边的元素必须是无理数。于是我们构造出了一个一一对应是从可数集到不可数集的，这显然是不可能的。

Problem 8:
若 $E \subset (0,+\infty)$ 中的点不能以数值大小排列，那么 $E' \ne \emptyset$ 。

还是一样，设 $E_n = \{x \in E : n-1 <x \le n\}$ ，那么 $E =\bigcup_{n=1}^{\infty}E_n$ ，那么存在 n_0 使得 $E_{n_0}$ 中的点不能以大小排列，那么就说明它是一个无限集。这样的话，因为每一个都是有限集，所以它必然存在一个极限点（B-W定理），那么自然 $E' \ne \emptyset$ 。

Problem 9:
若 $E \subset \mathbb{R}^2$ 中任意两点间的距离均大于1，那么是可数集。

这种点的距离的题目，我们要证明点可数，自然要把它与有理数联系起来，构造一个一一映射。而开球自然是非常好的方式。

因为有理数集的稠密性可知，对于任意的 $x \in E$ ，取 $r_x \in \mathbb{Q}^2$ ，都可以做到 $x \in B(r_x,\frac14)$ 。先证明 $B(r_x,\frac14) \cap B(r_y,\frac14)=\emptyset$ 。设 $z \in B(r_x,\frac14) \cap B(r_y,\frac14)$ ，那么 $|r_x-r_y| \le |r_x-z|+|r_y-z| <\frac12$ ，但另一方面 $|r_x-r_y| \ge |x-y| -|x-r_x|-|y-r_y| > 1-\frac14-\frac14=\frac12$ ，这就矛盾了。

所以这样的话，每一个就会对应一个独特的 $B(r_x,\frac14)$ ，但是 $\{B(r_x,\frac14)\}$ 是可数的，二者又是对等的，所以自然结论就成立了。

之后的几个题目会与开闭集，覆盖等内容有关。

Problem 10:
设 $F \subset \mathbb{R}^n$ 是闭集，，证明 $E=\{t \in \mathbb{R}^n:\exists x \in F ,s.t. ~ |t-x|=r\}$ 是闭集。

要证明一个集合是闭集，只需要说明 $E' \subset E$ 即可。

注意到，对于任意的 $t \in E'$ ，都存在 $\{t_k\} \subset E$ ，使得 $t_k \to t,k \to \infty$ 。那么由于 $t_k \in E$ ，所以存在 $x_k \in F$ ，使得 |x_k-t_k|=r 。根据 $\{t_k\}$ 可以一一对应得到一个数列 $\{x_k\}$ ，并且由 $\{t_k\}$ 有界可得 $\{x_k\}$ 也有界。那么必然存在收敛子列 $\{x_{k_j}\} \subset \{x_k\}$ ，使得 $x_{k_j} \to x,k_j \to \infty$ ，其中是这个数列的极限。且由于是闭集，可得 $x \in F$ 。那么进一步的，会有 $|x-t| = \lim _{k_j \to \infty}|x_{k_j}-t_{k_j}|=r$ ，这就证明了 $t \in E$ 。结论证完。

Problem 11:
设 $\{F_\alpha\}$ 为 $\mathbb{R}^n$ 中的一族有界闭集，若任取其中有限个 $F_{\alpha_1},F_{\alpha_2},\cdots,F_{\alpha_m}$ 都有 $\bigcap_{i=1}^{m}F_{\alpha_i}\ne \emptyset$ ，证明 $\bigcap_{\alpha}F_\alpha \ne \emptyset$

如果 $\bigcap_{\alpha}F_\alpha = \emptyset$ ，那么挑出其中任何一个 $F_{\alpha_0}$ ，都会有 $F_{\alpha_0} \cap (\bigcap_{\alpha \ne \alpha_0}F_\alpha) \ne \emptyset$ 。也就是 $F_{\alpha_0} \subset (\bigcap_{\alpha \ne \alpha_0}F_\alpha)^c=\bigcup_{\alpha \ne \alpha_0}F_\alpha^c$ 。注意到这是一个开覆盖，所以根据 $F_{\alpha_0}$ 是一个有界闭集可知存在有限的子覆盖 $\{F_{\alpha_i}^c\}_{i=1}^{m}$ ，使得 $F_{\alpha_0} \subset \bigcup_{i=1}^{m}F_{\alpha_i}^c$ 。这就说明 $F_{\alpha_0} \cap (\bigcap_{i=1}^{m}F_{\alpha_i})=\emptyset$ ，这就与题目条件矛盾了。

Problem 12:
设 $K \subset \mathbb{R}^n$ 是有界闭集， $\{B_k\}$ 是的开球覆盖，证明存在 $\epsilon>0$ 使得以中任何一个点为中心， $\epsilon$ 为半径的球一定含于 $\{B_k\}$ 中的一个。

根据覆盖的定义可知，对于任意的 $x \in K$ ，都存在使得 $x \in B_k$ ，也即存在 $\delta_x>0$ ，使得 $B(x,\delta_x) \subset B_k$ ，缩小开球的半径，可以得到 $K \subset \bigcup_{x \in K}B(x,\frac12 \delta_x)$ （事实上，缩不缩小半径，这都一定是对的）。所以存在一个有限的开覆盖，也就是 $K \subset \bigcup_{i=1}^{m}B(x_i,\frac12 \delta_i)$ ，那么再次根据覆盖的定义可得对于任意的 $x \in K$ ，存在 i_0 使得 $x \in B(x_{i_0},\frac12 \delta_{i_0})$ 。那自然存在也就有 $B(x,\frac12 \delta_{i_0}) \subset B(x_{i_0}, \delta_{i_0})=B_{i_0}$ （和第9题构造思路相同），所以这样子只需要令 $\epsilon = \frac12 \min \{\delta_1,\delta_2,\cdots,\delta_m\}$ 即可。

Problem 13:
设有 $\mathbb{R}$ 中的闭集F以及开集列 $\{G_k\}$ 。如果对于每一个都有 $\overline{G_k \cap F} = F$ ，那么有 $\overline {G_0 \cap F} =F$ 。其中 $G_0= \bigcap_{k=1}^{\infty}G_k$ 。

这个命题就相当于是说 G_0 在中稠密。那么要证明它自然只需要说明对于任意的 $x \in F$ 和 $\delta>0$ ，存在 $\xi \in G_0 \cap F$ ，使得 $|x-\xi|<\delta$ 。

从条件出发，取定 $x,\delta$ ，这样就给集合划分了一个范围，我们要去找这个 $\xi$ 。根据 $\overline {G_1 \cap F} =F$ 可知，这个范围内一定都会有 G_1 内的元素，也就是说存在 $x_1 \in G_1 \cap F$ ，使得 $x_1 \in (x-\delta,x+\delta)$ 。那么为了方便讨论，我们进一步做一个限制，取 $\delta_1 \in (0,\min \{\delta,1\})$ ，使得 $[x_1-\delta_1,x_1+\delta_1] \subset (x-\delta,x+\delta) \cap G_1$ （因为 x_1 本身也是开集 G_1 中的元素，所以根据开集的性质，取 $\delta_1$ 非常小的时候这是一定可以做到的）。按照同样的思路，根据 $\overline {G_2 \cap F} = F$ 可以推出来存在 $x_2 \in G_2 \cap F$ ， $\delta_2 \in (0, \min \{\delta_1,\frac12\})$ ，使得 $[x_2-\delta_2,x_2+\delta_2] \subset (x_1-\delta_1,x_1+\delta_1) \cap G_2$ 。

一直推下去就有对于任意的 $k \ge 2$ ，存在 $x_k \in G_k \cap F$ ，使得 $\delta_k \in (0,\min \{\delta_k,\frac1k\})$ ，使得 $[x_k-\delta_k,x_k+\delta_k] \subset (x_{k-1}-\delta_{k-1},x_{k-1}+\delta_{k-1}) \cap G_k$ 。所以说我们就构造出了一个有界递减闭集列 $\{[x_k-\delta_k,x_k+\delta_k]\}$ ，并且会存在 $\xi \in \bigcap_{k=1}^{\infty}[x_k-\delta_k,x_k+\delta_k] \subset \bigcap_{k=1}^{\infty}G_k=G_0$ 。又因为 $\{x_k\} \subset F,x_k \to \xi(k \to \infty)$ ，所以 $\xi \in F$ 。结合 $\xi \in [x_k-\delta_k,x_k+\delta_k] \subset (x-\delta,x+\delta)$ 即可得到结论。