经典网文分享: Note 0 经典场论对应的拉格朗日力学

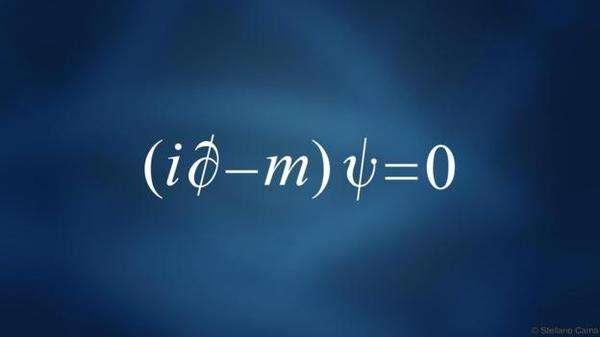
1、力学基础

在物理学中，最基本的经典力学量是作用量 S。作用量的定义是拉格朗日函数对时间的积分。

$S=\int Ldt\\$

拉格朗日函数 $L=L(q_\alpha,\dot q_\alpha,t)$ 是一个力学系统的特性函数，包含了一个力学系统的全部信息，对于连续的情况，拉格朗日函数可以写成以场为宗量的函数。这样拉格朗日可以写成拉格朗日密度函数对空间部分的积分，作用量可以写成

$S=\int Ldt=\int d^4x\mathcal L(\phi,\partial_\mu \phi) \\$

根据最小作用量原理，位形空间的路径对应于最小的作用量 S .这样有：

$\delta S=0\\$

$\delta S=\delta\int d^4x\mathcal L(\phi,\partial_\mu\phi)=\int d^4x\{\frac{\partial\mathcal L}{\partial\phi}\delta\phi+\frac{\partial\mathcal L}{\partial(\partial_\mu\phi)}\delta(\partial_\mu\phi)\}=0 \\$

对第二项应用一遍分部积分，很容易得到

$\delta S=\int d^4x\{[\frac{\partial\mathcal L}{\partial \phi}-\partial_\mu(\frac{\partial\mathcal L}{\partial(\partial_\mu\phi)})]\delta\phi+\partial_\mu(\frac{\partial\mathcal L}{\partial(\partial_\mu\phi)}\delta\phi)\}=0 \\$

第二项根据Stokes公式可以转化成表面积分，而在位形空间中 $t_1,t_2$ 点场的变分为 $0$ .

这样就得到了经典场的拉格朗日方程：

$\frac{\partial\mathcal L}{\partial \phi}-\partial_\mu(\frac{\partial\mathcal L}{\partial(\partial_\mu\phi)})=0\tag{1}$

比较于经典力学离散体系的拉格朗日方程：

$\frac{d}{dt}\frac{\partial L}{\partial \dot q_\alpha}-\frac{\partial L}{\partial q_\alpha}=0 \\$

场论里实质上是把场看成广义坐标，实际上在经典电动力学里我们就已经这样处理了（参考Jackson的电动力学狭义相对论部分）。很显然场在空间中是连续分布的，每一种场构型都对应着一个作用量，但是只有满足拉格朗日方程的场才能保证最小作用量。这也是经典力学所需要保证的。根据费曼路径积分公式:

$U(x_a,x_b;T)=\sum_{all\_paths}e^{i(phase)}=\int Dx(t)e^{i(phase)}\\$

这个phase实际上就是作用量 $S$ 。

显然如果作用量 $S$ 不是极小值，那么对于非最小作用量的路径来说，相位变化会剧烈变化以至于相互之间发生抵消。也就是说必须要有 $\frac{\delta S}{\delta x(t)}=0$ ，由此我们可以推导出拉格朗日方程，这就回到了本文刚开始。

对于给定的拉格朗日函数 $L=\int d^3x\mathcal{L}(\phi,\dot\phi)$ ,很自然我们可以定义正则动量

$p=\frac{\partial}{\partial\dot\phi}=\frac{\partial}{\partial\dot\phi}\int d^3y\mathcal{L}(\phi(y)\dot\phi(y))=\pi(x)d^3x\\$

这里 $\pi(x)=\frac{\partial \mathcal{L}}{\partial\dot\phi(x)}$ 叫做共轭正则动量密度。再根据勒让德变换带入拉格朗日方程 $(1)$ ，很快我们可得：

$H=\int d^3x\mathcal{H}=\int d^3x[\pi(x)\dot\phi(x)-\mathcal{L}]\tag{2}$

这样我们就得到了一个力学体系的另一个重要的特性函数——哈密顿函数

2、诺特原理

我们考虑一个空间连续分布的场 $\phi(x)$ ，其中它的无穷小变换形式为：

$\phi(x)\rightarrow\phi'(x)=\phi(x)+\alpha\Delta\phi(x)\\$

这里 $\alpha$ 是无穷小变换参数， $\Delta\phi$ 是场构型的"畸变"。力学里所谓的对称变换是指保持动力学方程形式不变的变换，这里我们的动力学方程是指拉格朗日方程。也就是说以上这种无穷小变换是保证了拉格朗日方程始终不变。

对于拉格朗日密度，我们考虑对应于场的无穷小畸变的导致的拉格朗日变化，近似到一阶。因为拉格朗日密度函数是洛伦兹不变的，也就是 $\mathcal{L}(x)\rightarrow\mathcal{L}'(x)=\mathcal{L}(\Lambda^{-1}x)$ 。这就要求拉格朗日密度的一阶项必须是一个四散度。

$\mathcal{L}(x)\rightarrow\mathcal{L}(x)+\alpha\partial_\mu\mathcal{J}^\mu(x)\\$

对 $\Delta\mathcal{L}$ 全微分展开，可以得到：

$\Delta\mathcal{L}=\frac{\partial\mathcal{L}}{\partial{\phi}}\Delta\phi+\frac{\partial\mathcal{L}}{\partial(\partial_\mu\phi)}\partial_\mu(\Delta\phi)\\ =\partial_\mu(\frac{\partial\mathcal{L}}{\partial(\partial_\mu\phi)}\Delta\phi)+[\frac{\partial\mathcal{L}}{\partial\phi}-\partial_\mu(\frac{\mathcal{L}}{\partial(\partial_\mu\phi)})]\Delta\phi\\$