经典网文分享: 声子偏振子 (phonon polariton)

这学期的期末大作业做的是声子偏振子，在整理做ppt之前先用母语打一遍草稿吧233333（传说中的写英文报告之前用中文写再翻译避免抄袭大法好……）

偏振子(polariton, 但愿是这个翻译，并不确定……)是由电磁波和材料中的某种"激发"强耦合产生的一种粒子，例如声子与光子强耦合产生的声子偏振子(phonon polariton)、激子与光子强耦合产生的激子偏振子(exciton polariton)等等。这里要注意区分偏振子和极化子(polaron)，前者是玻色子，而后者是费米子(例如电子和光子的强耦合)，描述存在很大的区别。学识有限，以下我们只考虑声子偏振子。

本文将从经典的电磁学推导出发，得出由于声子偏振子而带来的反常色散曲线。接着，本文使用Hamiltonian将光学模和声学模本征值分解（类似于二次量子化），得出完全一致的结论，并将声子偏振子与腔光力学(cavity optomechanics)系统中的强耦合建立联系(exactly the same)。接着本文将讨论由声子偏振子产生的一些有意思的现象和可能的应用，例如LO-TO模式分离、偏振子-光子晶体、表面声子偏振子以及声子偏振子的声子对应。

这么长大概没人看吧……希望我的这么少工作量的作业期末能混过去啊Orz……弱鸡到期末觉得心力交瘁四处漏风要猝死了……

1. 传统的电极化推导方法

我们首先从最传统的固体物理课本[1]出发。让我们假设有一个离子晶体，晶体中的离子永远处于无休止的振动状态……由于我们希望离子的振动与光子能够达到强耦合，因此振动的能量和动量最好和光子相似。为了达到与光子相似的能量，我们不得不考虑频率更高的声子——光学声子(THz数量级，与红外光的频率相当)，材料中声学声子的振动频率太过缓慢，一般无法直接与光子发生耦合。对于THz的光子，可以计算出来它的波矢( $k=\omega / c$ )十分小，因此我们可以放心大胆的使用长波近似进行以下讨论啦～

首先从最简单的双离子晶体——NaCl出发。在外加电场 $E=E_0 e^{jωt}$ 的作用下，晶体中的一个离子的运动方程可以写为：

$M\ddot{u}+Mω_T^2 u=qE$

因此我们可以算出由这个过程所导致的电极化强度 $P=Nqu=\frac{Nq^2}{M} \frac{1}{(ω_T^2−ω^2 )} E$ 。由最终的电场 $D = \epsilon(\omega) E = \epsilon(0) E + P$ ，可以得到：

$\epsilon(\omega)=ϵ(∞)\frac{ω^2−ω_L^2}{ω^2 - ω_T^2}$

以及大名鼎鼎的LST关系：

$\frac{ω_L^2}{ω_T^2}= \frac{ϵ(0)}{ϵ(∞) }$

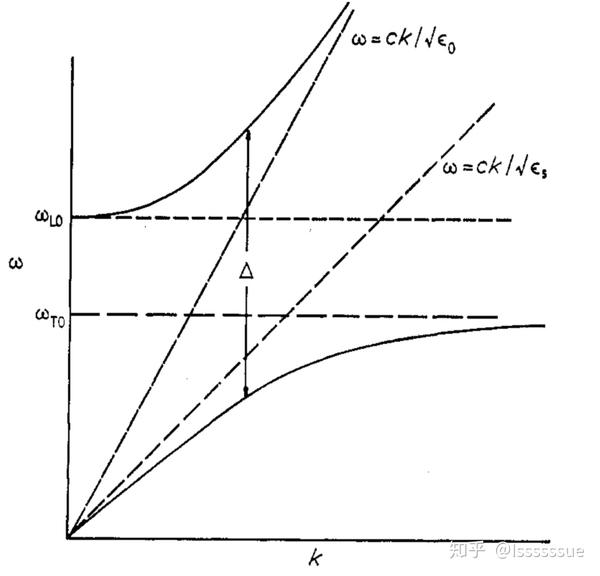
由这个可能为负数的介电常数 $\epsilon(\omega)$ ，可得到这个漂亮的色散曲线，曲线之中 $\omega_T - \omega_L$ 的区域将会产生纯虚数的折射率，成为一个"偏振子禁带"(Reststrahlen band)，带来很多有意思的现象：

2. 汉密尔顿量推导

上面的推导实在太经(wu)典(liao)了……作为一个会特征值分解的少年，自然应尝试一下使用类似于"量子化"的方式推导出同样的结论。本文谨参考Hopfield model[3]进行一系列计算，此外还参考了[4]。

根据Hopfield model(没错就是那个递归神经网络的Hopfield，他老人家是物理教授出身 )，我们可以将这个系统看作一群(N个)谐振子们和光场的相互作用，由此可以列出它的总能量应该是

$H=\sum_{l=1}^N \left[ \frac{p_l^2}{2m}+\frac{m \omega_T^2}{2} x_l^2 −e x_l 𝐸(r_l) \right] + \frac{1}{2\mu_0} \int dr^3 B(r) \cdot B(r)+\frac{1}{2\epsilon_0 }\int dr^3 D(r) \frac{ 1}{\epsilon(r)} D(r)$

使用特征模分解的方法，我们可以把这个很麻烦的汉密尔顿量写作（这个部分可以参考我之前的一个知乎回答或者直接看论文吧hhhh）：

$H=\sum_{l=1}^N \omega b_l^* b_l −\frac{e}{\sqrt{2} \beta } (b_l + b_l^* )E(r_l )+\sum_\lambda \sum_k ck a_{\lambda k}^* a_{\lambda k}$

$\lambda$ 代表偏振方向。通过一系列神乎其技的化简以后，我们可以得到如下式子：

$H=\sum_\lambda \sum_k \omega b_{\lambda k}^* b_{\lambda k } + ck a_{\lambda k}^* a_{\lambda k} + const \times (b_{\lambda k} a_{\lambda -k}+b_{\lambda k}^* a_{\lambda k} - b_{\lambda k}^*a_{\lambda -k} ^*- b_{\lambda k} a_{\lambda -k}^* )$

这个式子格外的眼熟，让人一秒就想到腔光力学的那个经典方程[5]：

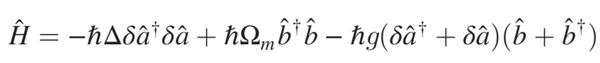
但这里有一点点小区别：由于腔光力学中的声子振动频率较小，事实上在腔光力学系统之中，与声子产生强耦合的是泵浦光和信号光的拍频！如果把这个拍频换成在我们体系之中的电磁波，把那个能量弱爆了的声子换成我们体系之中的棒棒哒光学声子，其实我们的系统和腔光力学系统并没有什么区别，强耦合的腔光力学系统其实也就只是一个声子偏振子罢了。

由于我们处于强耦合状态，不能直接认为相互作用前后的光子模和声子模不变: 过强的耦合将使得两个模式融合在一起，它们各自携带对方的信息，此时rotating wave approximation将完全不再适用。为了算出我们未来系统的本征值，我们可以将此时的汉密尔顿量对角化，成为如下形式：

$H=\sum_\lambda \sum_k [ \Omega_+ (k) c_{\lambda k}^\dagger c_{\lambda k} + \Omega_- (k) c_{\lambda -k}^\dagger c_{\lambda -k} ]$

$\Omega_\pm$ 可以直接通过原来的哈密尔顿量算本征值直接求出，经过比对可以发现和经典方法所得到的完全一样。这个时候的新模 $c_{\lambda k}$ 相当于是光子模和声子模的融合，当 $\omega$ 远离 $\omega_T$ 和 $\omega_L$ 这两个特殊量时，可以认为新模约等于纯粹的光子模（或声子模），即此时的耦合量过小，对于系统的影响可以忽略不计。

事实上，这个问题可以用量子力学之中的"反交叉"原则(avoided crossing / anticrossing)来解释：对于一个双能级的系统，如果我们给汉密尔顿量加两个非对角项的微扰，那么新的汉密尔顿量本征值(即新的能量)将可以计算如下：

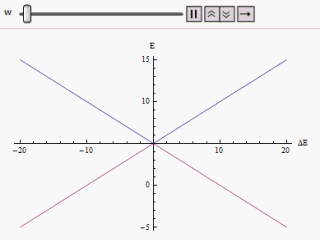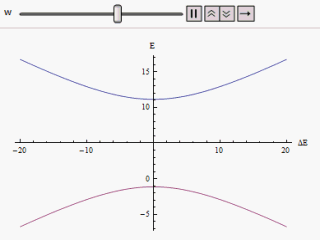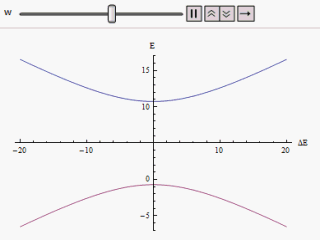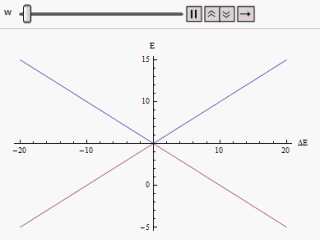
由图中我们可以看出，随着微扰w的升高，双能级的交叉会得到避免，且越走越远；当微扰为0时，两个能能级将会相互交叉。这个原理会带来一个特别有意思的现象，我们在下一节会进行仔细分析。

3. LO-TO分离

考虑两个结构相似的晶体：金刚石和BN。两者的能带结构却十分不相同（红色圆圈处）：

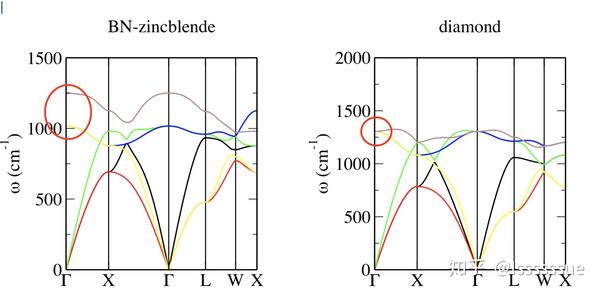
这个问题并不trivial。根据理论计算，金刚石型的立方晶体结构要求LO模和TO模在 $\Gamma$ 点处简并，即BN之中的LO模和TO分离本应不可能发生。该如何解释这个现象呢？若在"放缩"到其他参数一致的金刚石和BN之中考虑长波纵模，因为BN是极性材料，在纵模的振动过程之中，将会有电偶极子被不断产生和消灭，电偶极子和电偶极子的相互作用会带来额外的能量，然而横模就不存在这个问题，于是BN的横纵模就会分离了……

然而金刚石不是极性材料，它并不存在这个问题。

我们也可以从"反交叉"原则来理解这个问题：在非极性物质之中，对于汉密尔顿量的非对角微扰将会消失，此时的能级必然相交如上上图……

如果想更定量的去算的话，这个问题是density functional perturbation theory之中的一个经典问题，可以去看看……由于我弱智，没看懂= =

4. 偏振子-光子晶体

嗯，这个部分是让我最感兴趣的一块了！光子晶体本身就会产生禁带，而偏振子又会给它带来额外的禁带，两种禁带加在一起，事情就会变的interesting起来～

下图是经计算得到的一维CsI偏振子-光子晶体的能带：

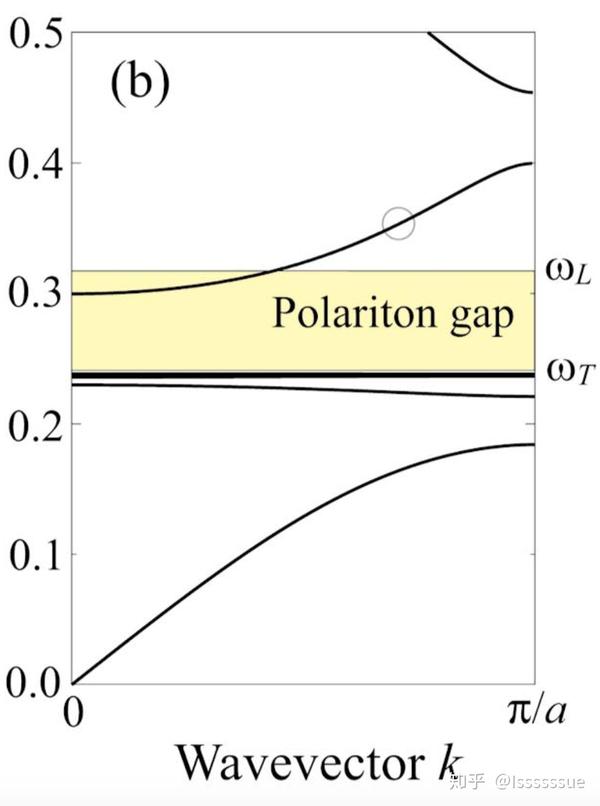
这个图中有三个很有意思的地方：

1) 在 $\omega_T$ 下方的平带

我们可以由LST关系得知，当频率趋近于 $\omega_T$ 时，介电常数趋向于正无穷，即折射率n也会趋向于正无穷。由此，在CsI与空气的交界处，反射率 $R= \left| \frac{n-1}{n+1} \right|^2$ 趋向于1，即所有的波都会被反射回来集中在介质之中(对于 $n<\infty$ ，会有少量光场泄漏到空气之中，从而使得相邻的介质块得以互相耦合)。此时介质之中只能存在驻波， $\omega_m = \frac{m \pi c}{nd} = \frac{m \pi c}{\sqrt{\epsilon(\omega)} d}$ ，形成在偏振子禁带下方的一系列平带。

2) 在 $\omega_L$ 附近出现的禁带中的模

可以将这个模理解为因为空气造成的缺陷而在偏振子材料之中形成的新模。该模会在介质之中衰减。

3) 在 $\omega_L$ 附近出现的"透明点"

这个点对应于介电常数为1的点，可以通过人为调控晶体的结构、晶体的材料等改变位置，从而改变这个点的折射率改变速度。

当把以上的一维晶体变成二维晶体，可以调控的量就会更多，可以产生一些有趣的现象。

5. 表面声子偏振子 (surface phonon polariton, SPhP)

由于SPhP的存在，使得介电常数可以为负，这不禁让人想起了"表面等离激元"(surface plasmon, SPP)的产生。表面声子偏振子的色散关系如图：

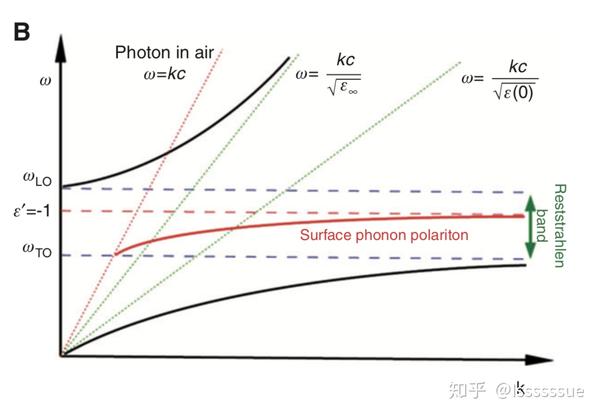
当一束频率处于偏振子禁带之中的电磁波打到材料上时，能够激发材料表面的离子与电磁波共振，但由于此时的介电常数为负，该声子偏振子将无法向材料深处传播，形成SPhP，色散关系如图。与SPP相比较，由于SPhP的损失主要来自于光学声子的散射，而SPP的损失主要取决于自由载流子的寿命，因此SPhP的损失更小，寿命更长(ps量级)。此外，SPhP的波长更长，与主要在可见光和近红外的SPS不同，它的波段集中在中红外。

6. 偏振子间的相互作用

事实上，一些常见的非线性现象，例如二次谐波产生、和频产生等等，其实如果发生在THz波段，都需要考虑偏振子对于结果的影响。由于色散曲线存在两支，相位匹配将不会是普通的近乎线性的关系，而可能是不同支的点的相互叠加。这些情况都要具体计算具体分析。

一个尤其有趣的点是双光子吸收。在吸收两个光子以后，被激发到导带的电子和禁带中生成的空穴形成激子，而这个激子又可以和光子耦合形成激子偏振子(exciton polariton)，最终这个过程可以看作三个偏振子之间的相互作用！对这样的情况，光的色散曲线需要重新讨论。

7. 碎碎念

看文献[2]看到一个很有意思的想法。声波的方程和光波其实是几乎完全一致的，二者二次量子化后的结果分别是声子和光子，也都是玻色子。因此上面的所有讨论都可以直接类比到材料之中的声学声子上去……当材料之中有某种"激发"的频率和波矢达到和声学声子相似的量级，以至于形成强耦合时，也将形成属于声子的偏振子。

一个比较典型的例子，大概就是磁振子和声子的相互耦合了……二者都是玻色子，强耦合时的方程和前面的推导一模一样，不过如果这样说的话那所有的强耦合其实都是一样的= =这个topic太大了估计得再做好几个project才能看懂呢……

Reference:

Kittel, Solid State Physics.
D L Mills, Polaritons: the electromagnetic modes of media, 1974, Rep. Prog. Phys 37 817
J J Hopfield, 1958, Phys. Rev. 112, 1555
A R Navin, 2006, PHYSICAL REVIEW A, 73, 063808
Markus Aspelmeyer, 2014, Rev. Mod. Phys. 86, 1391
K C Huang, 2003, PHYSICAL REVIEW B, 68, 075209
J D Caldwell, Low-loss, infrared and terahertz nanophotonics using surface phonon polaritons, 2014, Nanophotonics

***** 最后的最后……借知乎吐一下槽，都不敢发微信了……真的有人读博读的我这么烂吗？觉得周围的人都发paper开会的就差上天了，而我连英语和期末考试这两项最basic的东西都搞不定，每天都活在极度的自我厌恶之中，简直怀疑自己的智商在决定读博的那一刻和自信一起私奔了……

事情不会靠无数的鸡汤好起来……每天睁开眼想到没做完的一系列事情都希望永远睡死过去……

来源：知乎 www.zhihu.com
作者：知乎用户（登录查看详情）

【知乎日报】千万用户的选择，做朋友圈里的新鲜事分享大牛。点击下载

经典网文分享

声子偏振子 (phonon polariton)