经典网文分享

本文主旨在于分析NB对VP的第三场比赛

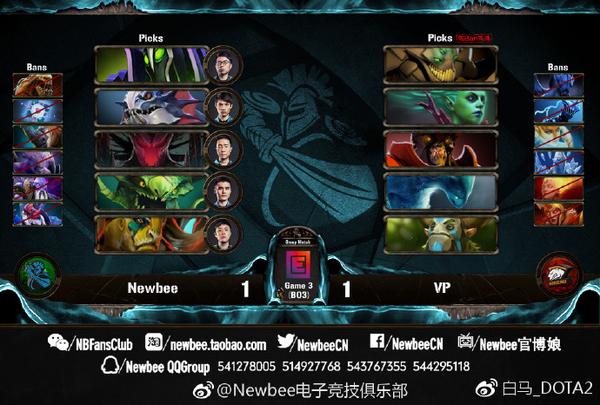
说实话，看到NB选择在第五手Ban位禁掉黑贤，然后在三手点出TB的时候，我是非常震惊的

我相信一个对于DOTA2有深刻理解的BP手，是不可能在己方要选择TB作为核心，同时对手已经选出来沙王这样的一个先手点时，放出末日这个极强的单体控制英雄。

沙王+末日+水人，这三个英雄的组合是完全将TB吃死了。

在中后期的任何一场团战里，只要沙王先手晕到TB，帮助末日定位，末日跟上一个大招，水人开着BKB就可以肆意的冲进战场把TB按死在地上，而NB的阵容里，没有任何一个人能够拯救这种局势

相较于TB在团战中只要被沙王先手，没开出BKB就GG，哪怕开出BKB也有被末日大到然后被水人+死亡先知大招 A死的恶劣环境，水人这把有着无限的发挥空间。除非被拉比克偷到末日大，还要配合大鱼的先手点灯破林肯。只要开着BKB，没有任何人可以在团战中阻当这个水人。

水人可以非常从容的选择切入后排用虚灵刀秒掉对面辅助，或者是等待沙王先手、末日大到TB\骗出TB的BKB，等待BKB结束，再波上去输出。他可以在团战中静心等待无数的可能发生，再选择其中的最优解。

因为有DP在前面给他撑住局势，创造空间。

而毒龙能够在团战中帮TB撑住吗，能够帮TB吃掉沙王的先手、逼出末日的大招，顶住死亡先知大招的伤害，给TB创造出空间吗？

——他本应可以的，只要他的发挥足够出色。

我非常费解，为什么在看到沙王+末日的先手组合，并且对面中单已经暴露的情况下，要选择毒龙这样一个英雄，而不是另一个更好的选择

黑鸟？不仅可以救TB，逼出末日的大招，还能在对线DP的时候不落下风，VP也不敢选择水人这样的一个血少爆发高核心

火枪？对线大优，第二输出点，哪怕TB的发挥空间被无限压缩，团战还存在另一个输出核心，还有赢下团战的可能。

老鹿？对线至少小优，多一个前期的节奏点和推进点，给TB拉扯出足够的空间，打团也能帮TB吃技能。
(......)

NEWBEE在中单的选择上明明有着更广袤的空间，更多更好的选择，却最后做出了毒龙这样一个让人难以理解的选择。

对于一个备受期待的顶尖强队来说，科学、系统的BP策略是必须要具备的。

我不知道NB是否还停留在五个人聚在一起，队员互相讨论一下，然后说"给我选毒龙、TB，我这个英雄绝活"，队长稍微思考一下，看着眼前的选人觉得队员说自己绝活，选出来好像也还不错，然后就点出来的原始BP阶段。

但从结果上来说，这局的BP，Newbee不合格。

BP出来的结果是死的，但分路、打法是活的，是还可以从中创造出空间的。

从这个阵容来说，如果水人经济落下，输出不足，TB无解肥，装备成型。哪怕TB吃了末日大，水人波上去打不死TB，反而可能被TB配合大牛光环直接打死。DP也没法那么从容的在前线顶着TB的输出拉扯空间。

那么按照这个思路来想，TB带大牛拉比克刚三，大鱼打三单末日会是一个更好的选择，至少要比TB拉比克在下路打沙王末日的双劣，结果TB对线期连死三次要好的多。

然后NB选择大牛大鱼双劣打水人，下路TB拉比克打末日大鱼，中路毒龙SOLO死亡先知。接着VP按照这个分路，对应的是水人抗压，先知解放成自由人。

于是这个被解放的先知，3分42秒在下路杀了TB，4分33秒在中路杀了毒龙，6分21秒又在下路把TB再杀一次。

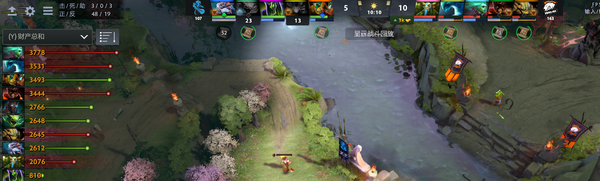
10分钟的时候，抗压的水人经济第二，五号位先知领先对面五号位1200经济，两个中单有1100的经济差。

这很大程度上，是因为被解放的先知游走带来的效果，但NB也不是没有过通过游走打开局势的机会。

6分钟的时候，4级的大鱼隐身在死亡先知身边，死亡先知身上的TP还放在背包里面，如果配合毒龙是完全有机会击杀的，但卡卡却没有选择动手。

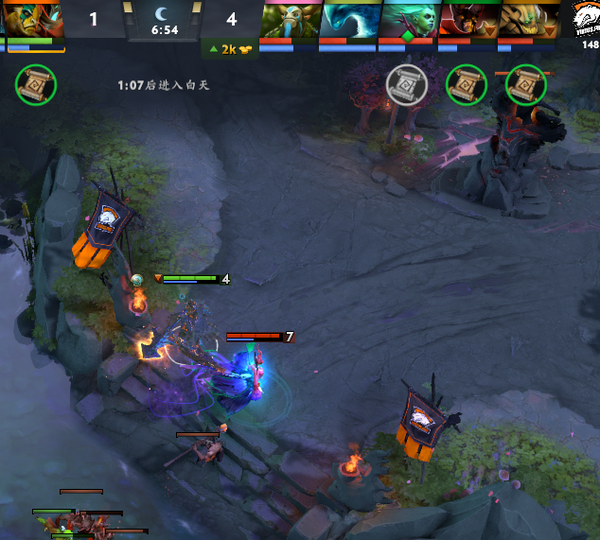
因为毒龙这个时候只有5级

为什么毒龙这个时候只有5级？

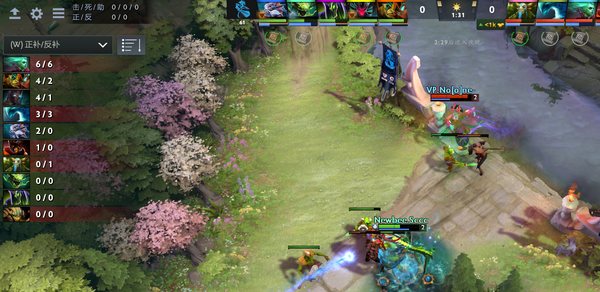
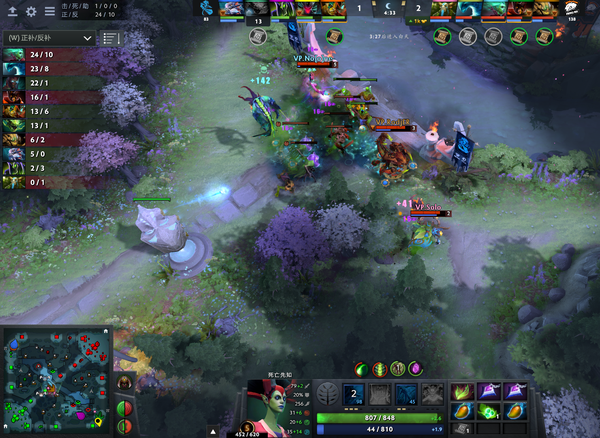
这是开局1分30秒和4分33秒毒龙第一次被游走时的补刀对比。

这是我看过所有比赛当中，优势英雄对线时，最夸张的补刀对比。

我相信不需要我再说明为什么NB在十分钟的时候，会跟VP有3000的经济差了。

最后再谈一点

这是二十分钟的时候。双方的眼位对比图。希望NB下次能够意识到，在对面有先知的时候，看看自己的高地上是不是已经有对面的假眼了。

不然在这样的顶尖强队对抗中，BP被爆、对线被爆、视野还被爆，凭什么赢？

肉山团？

希望Newbee能够在以后的比赛中，将自己的不足之处，像已经越打越好的肉山团一样弥补过来，让观众一起看到NB的成长。

感谢您的阅读，愿NB在震中杯之后的比赛中能够越打越好。

来源：知乎 www.zhihu.com
作者：白马

【知乎日报】千万用户的选择，做朋友圈里的新鲜事分享大牛。点击下载

玩计算器的发现

大家都玩过计算器吧, 不知注意到没有.

输入任意数, 然后不断按 $\mathtt{cos\ ANS}$ 最后总会输出 $0.739085$ .

什么, 你说明明记得是: $0.999847$ ? 哦, 因为你用了角度制.

这一系列操作等价于求解方程 $x=\cos x$ , 角度制下就是 $x=\cos x°=\cos\dfrac{\pi x}{180}$ .

当然对于现在的你来说求数值解没啥意思了, 要求就求解析解是吧.

不过这两个方程其实是一样的, 我们先变个形:

$\begin{aligned} x=\cos x\;\Longrightarrow& x-\frac{\pi}{2}=\cos \left(x-\frac{\pi}{2}\right)&=\sin x\\ x=\cos x°\Longrightarrow& \frac{180 x}{\pi }-90=\cos \left(\frac{ \pi}{180} \left(\frac{180 x}{\pi }-90\right)\right)&=\sin x \end{aligned}$

也就是说:

于是我们现在只要解决 $Ax-B=\sin(x)$ 这一个方程了.

最早研究这个问题的是天文学家, 毕竟那时候也没什么计算器给你玩, 一切要从实际出发...

开普勒方程

你可能听说过, 三体问题很困难, 直到一百多年前的庞加莱时代才被搞定.

而二体问题则简单的多, 400年前开普勒时代就研究的差不多了.

你至少知道这个成果, 两个天体以一个为交点, 另一个必定在圆锥曲线上运动.

一般天体遵循椭圆轨道, 如图椭圆是实际运行的轨道, 与椭圆相切的是一个以半长轴为半径的辅助圆.

在一定的时间 $t$ 内, 椭圆轨道上的质点运行到了 $p$ 点, 而辅助圆上的假想质点运行到了 $y$ 点.

椭圆轨道上所转过的角度 $\angle T$ 被称为真近点角(True Anomaly)
辅助圆轨道上假想质点所转过的角度 $\angle M$ 被称为平近点角(Mean Anomaly)
将椭圆上的质点向上作延长线,交辅助圆于 $x$ 点所形成的角 $\angle E$ 被称为偏近点角(Eccentric Anomaly)

天文学家发现, 它们满足如下关系式:

Kepler Equation: $M= E-\epsilon \sin(E)$

抛物线就是 $\epsilon=1$ 的特殊情况, 双曲线有所不同.

Hyperbolic Kepler Equation: $M = \epsilon \sinh H - H \quad\mathrm{where}\quad H=iE$

但从数学上讲, 这个式子其实就是:

$M = i \left( E - \epsilon \sin E \right)$

也就是说不考虑物理意义其实是一样的.

开普勒方程的解析解

有了方程当然接下来就是求解了咯, 古代计算力比较值钱, 毕竟没有计算机, 所以大家对解析解都有一种病态的追求.

怎么着推一天公式要比算一整天的牛顿迭代有趣吧?

$\left\{\begin{aligned} \frac{\pi}{2}&=x-\sin x\\ \frac{\pi}{2}&=x-\frac{\pi}{180}\sin x \end{aligned}\right.$

作一下等价性检验:

In [] = FindRoot[x==Cos@x,{x,0}]          x-Pi/2/.FindRoot[Pi/2==x-Sin@x,{x,1}]          FindRoot[x==Cos[Pi x/180],{x,0}]          180x/Pi-90/.FindRoot[Pi/2==x-Pi Sin@x/180,{x,1}]    Out[] = 0.7390851332151605`           {x -> 0.7390851332151607`}           0.9998477415310987`           {x -> 0.9998477415310881`}

拉格朗日反演

$E$ 不能分离但 $M$ , 展开 $M(E)$ ,然后直接用级数反演即可.

$M(E) = (1-\epsilon)E+\epsilon\sum _{n=1}^{\infty } \frac{(-1)^n}{(2 n+1)!}E^{2 n+1}$

$\bigstar E(M)= \begin{cases} \displaystyle \sum _{n=1}^{\infty }\bigg(\lim_{\theta \to 0^{+}}\!{\frac {\mathrm {d} ^{\,n-1}}{\mathrm {d} \theta ^{\,n-1}}}{\bigg (}{\frac {\theta }{\sqrt[{3}]{\theta -\sin(\theta )}}}{\bigg )}^{\!\!\!n}{\bigg )}{\frac {M^{\frac{n}{3}}}{n!}}&\epsilon=1\\ \displaystyle \sum_{n=1}^{\infty }\bigg(\lim_{\theta \to 0^{+}}{\frac {\mathrm {d} ^{\,n-1}}{\mathrm {d} \theta ^{\,n-1}}}{\Big (}{\frac {\theta }{\theta -\epsilon\sin(\theta )}}{\Big )}^{\!n}{\bigg )}{\frac {M^{n}}{n!}}&\epsilon\neq 1 \end{cases}$

Mathematica 可以很方便的执行级数反演.

Series[M-  Sin[M], {M, 0, 10}]//InverseSeries  Series[M-e Sin[M], {M, 0, 10}]//InverseSeries

早期解这个方程使用了关于离心率 $\epsilon$ 的麦克劳林展开.

$E(M)=M+\sum_{n=1}^\infty a_n \epsilon^n;\ \epsilon\leq\mathrm{L}$

这不是个整函数, 所以引入了所谓的拉普拉斯极限.

$L=\max_{x\in\mathbb{R}}\frac{x}{\cosh (x)}\approx0.662743$

超出收敛域的部分级数失效, 级数反演则很好的解决了这个问题.

贝塞尔函数解

当然无穷级数不利于计算, 能否使用微积分表达是我们接下来的探索重点.

我们来考虑函数方程: $g (M) = E (M) - M$

我们假设它可以展开为傅里叶级数, 分析原函数方程性态可以期望这是个正弦级数.

$g (M) = \sum_{n = 1}^{\infty}a_n\sin (n M)$

那么系数可以表达为:

$a_n = \frac {2}{\pi}\int_0^\pi g(M) \sin(nM)\,\mathrm{d}M$

我们来尝试计算, 嗯? 没思路怎么办...

无脑分部积分展开到能搞定为止呗.

$\begin{aligned} a_n&=\frac{2}{\pi n}\int_0^\pi \cos(nM)\,\mathrm{d}g(M) -\frac{2}{\pi}\left[g(M)\frac{\cos(nM)}{n}\right]_0^\pi\\ &=\frac{2}{\pi n}\int_0^\pi \cos(nM)\,\mathrm{d}(E-M)\\ &=\frac{2}{\pi n}\int_0^\pi \cos[n(E-\epsilon\sin E)]\,\mathrm{d}E -\frac{2}{\pi n}\int_0^\pi \cos(nM)\,\mathrm{d}M\\ &=\frac{2}{\pi n}\int_0^\pi \cos(nE-n\epsilon\sin E)\,\mathrm{d}E \end{aligned}$

而这正好是贝塞尔函数的定义式之一:

Bessel Function of the First Kind: $J_n(z)=\frac{1}{\pi}\int_0^\pi \cos(n θ-z \sin θ)\,\mathrm{d}θ\ ;n\in \mathbb{Z}$

于是原式可以写成

$\bigstar E(M)=M+\sum _{n=1}^{\infty } \frac{2}{n}J_n(n \epsilon )\sin(nM)$

赫维茨-勒奇超越函数解

Stack Exchange上有个用反三角函数和三角函数表示的解析解, 这个解比较有难度.

$\mathcal{D}=\frac1\pi \int_0^{\pi } \arctan\left(\tan \left(\frac{t-\sin t+\frac{\pi }{2}}2\right)\right) \,\mathrm{d}t+\frac{1}{\pi }$

特殊函数论中将以下级数称为赫维茨-勒奇超越函数(Lerch Transcendent Function)

$\Phi (z,t,h):=\sum _{n=0}^{\infty } \frac{z^n}{(h+n)^t}$

我们从上面的贝塞尔函数解开始, 还原掉贝塞尔函数:

$E=M+\sum _{n=1}^{\infty } \frac{2}{n}\left[\frac{1}{\pi}\int_0^\pi \cos(n θ-n\epsilon \sin θ)\,\mathrm{d}θ\right]\sin(nM)$

然后交换积分求和顺序.

$E=M+\frac{2}{\pi}\int_0^\pi\left[\sum _{n=1}^{\infty } \frac{\sin(nM)}{n} \cos(n θ-n\epsilon \sin θ)\right]\,\mathrm{d}θ$

里面的部分圈起来叫 $F(M)$ , 用欧拉公式展开. $\begin{aligned} F(M)=&\frac{\sin(nM)}{n} \cos(n θ-n\epsilon \sin θ)\\ =&\frac{i}{4 n}\left(e^{-i M n}-e^{i M n}\right) \left(e^{-i (\theta n-n \epsilon \sin (\theta ))}+e^{i (\theta n-n \epsilon \sin (\theta ))}\right)\\ =&\frac{i}{4 n}\left(e_1+e_2+e_3+e_4\right) \end{aligned}$

其中:

$\begin{cases} e_1=+\exp(-i M n+i \theta n-i n \epsilon \sin (\theta ))\\ e_2=-\exp(i M n+i \theta n-i n \epsilon \sin (\theta ))\\ e_3=+\exp(-i M n-i \theta n+i n \epsilon \sin (\theta ))\\ e_4=-\exp(i M n-i \theta n+i n \epsilon \sin (\theta ))\\ \end{cases}$

可以发现其实都是 $e^{n\alpha}$ 的结构.

我们引入多对数函数:

$\mathrm{Li}_s(z) := z\Phi (z,s,1)=\sum _{n=1}^{\infty } \frac{z^n}{n^s}$

也就是说:

$\sum _{n=1}^{\infty } \frac{e^{a n}}{n}=\text{Li}_1\left(e^a\right)=i\arg (1-e^a)-\ln |1-e^a|$

用这个函数化简等式:

$\begin{aligned} E=&M+\frac{2}{\pi}\int_0^\pi\left[\sum _{n=1}^{\infty } \frac{i}{4 n}\left(e_1+e_2+e_3+e_4\right)\right]\,\mathrm{d}θ\\ =&M+\frac{i}{2\pi}\int_0^\pi\left[\text{Li}_1(e^{a_1})+\text{Li}_1(e^{a_2})+\text{Li}_1(e^{a_3})+\text{Li}_1(e^{a_4})\right]\,\mathrm{d}θ \end{aligned}$

同样的整理一下:

$\begin{cases} a_1=+i (\theta -M-\epsilon \sin (\theta ))\\ a_2=+i (\theta +M-\epsilon \sin (\theta ))\\ a_3=-i (\theta +M-\epsilon \sin (\theta ))\\ a_4=-i (\theta -M-\epsilon \sin (\theta ))\\ \end{cases}$

可以合并成两组, 然后再次展开, 运算量有点大.

化简的时候注意恒等式: $\arg(e^{ix})=\arctan(\tan (x))$ .

$\begin{aligned} \sum \text{Li}_1(e^{a}) =&\frac{2}{i}\arctan\tan \left(\frac{\theta -M-\epsilon \sin (\theta )+\pi}{2} \right)\\ +&\frac{2}{i}\arctan\tan \left(\frac{-\theta -M+\epsilon \sin (\theta )+\pi}{2}\right) \end{aligned}$

注意到第二部分:

$\int_0^{\pi } \arctan\cot \left(\frac{1}{2} (\theta +M-\epsilon \sin (\theta ))\right) \, \mathrm{d}\theta =\epsilon+\frac{1}{4} \left( +\pi ^2-2 \pi M\right)$

最后代回去大功告成!

$\begin{aligned} \bigstar E=&M+\frac{i}{2\pi}\int_0^\pi\sum \text{Li}_1(e^{a})\,\mathrm{d}θ\\ =&\frac{1}{4} (2 M+\pi )+\frac{\epsilon }{\pi }+\frac{1}{\pi }\int_0^\pi\arctan\tan \left(\frac{\theta -M-\epsilon \sin (\theta )+\pi}{2} \right)\mathrm{d}\theta \end{aligned}$

代入数据就得到了 Stack Exchange 一样的结果.

我对 $\arctan(\tan (x))$ 这种写法感到很不爽.

这个当然不能直接抵消, 由于 $\arctan(\tan (x)) \neq x$ , 我们作复展开.

$\begin{aligned} \arctan(\tan (x)) &=\frac{1}{2} i \log \left(1+\frac{e^{-i x}-e^{i x}}{e^{-i x}+e^{i x}}\right)-\frac{1}{2} i \log \left(1-\frac{e^{-i x}-e^{i x}}{e^{-i x}+e^{i x}}\right)\\ &=\frac{i}{2}\log \left(\frac{2}{1+e^{2 i x}}\biggl/\frac{2 e^{2 i x}}{1+e^{2 i x}}\right)\\ &=\frac{i}{2}\log (e^{-2 i x}) \end{aligned}$

严格来说这两者不是完全相等的, 因为这样一来消掉了奇点.

不过积分的时候完全可以划等号, 因为区间开闭完全不影响积分值.

$\bigstar E=\frac{1}{4} (2 M+\pi )+\frac{\epsilon }{\pi }+\frac{i}{2\pi }\int_0^\pi \log \left(-e^{i (M+\epsilon \sin\theta-\theta)}\right)\mathrm{d}\theta$

综上所述, 最后代入值, 我们得到了:

$\begin{aligned} \mathcal{D}_{\;}=&\frac{1}{\pi }\left[1+\frac{i}{2}\int_0^{\pi}\log \left(-i e^{i (\sin t-t)}\right)\;\mathrm{d}t\right]\\ \mathcal{D}_°=&\frac{1}{\pi }\left[1+\frac{90i}{\pi}\int_0^{\pi}\log \left(-i e^{i (\pi\sin t/180-t)}\right)\;\mathrm{d}t\right] \end{aligned}$

(*真男人从不回头看数值验证*)  (2 + I Integrate[Log[-I/E^(I*(t - Sin[t]))], {t, 0, Pi}])/(2*Pi)//N  (Pi + 90I Integrate[Log[(-I)*E^((-I)*t + (1/180)*I*Pi*Sin[t])], {t, 0, Pi}])/Pi^2//N    > 0.7390851332151609`   > 0.9998477415310951`

只有娘们才喜欢用特殊函数

最后一个是百度贴吧上的, 这个答案就非常魔幻了,它和上面两个方法不是一个系列的, 和第一个方法有关.

暴力求解拉格朗日反演的解析形式, 场面非常的少儿不宜...

我一时半会儿也没看懂,详情看参考书目(3).

$\begin{aligned} \mathcal{D}=&\frac{1}{2} \pi \exp \left(\int_0^1 {\frac{1}{\pi x}\arctan\left(\frac{x \log \left(\frac{\sqrt{1-x^2}+1}{x}\right)(\pi x+2) }{x^2 \log ^2\left(\frac{\sqrt{1-x^2}+1}{x}\right)-\pi x-1}\right) \, \mathrm{d}x}\right)\\ =&\mathrm{arccot}\left(1+\frac{1}{2 \pi }\int_0^1{ \log \left(\frac{\pi ^2 \left(1-x^2\right)+4 \left(\sqrt{1-x^2} \mathrm{arctanh}(x)+x\right)^2}{\pi ^2 \left(1-x^2\right)+4 \left(\sqrt{1-x^2} \mathrm{arctanh}(x)-x\right)^2}\right) \, \mathrm{d}x}\right) \end{aligned}$

从这个结果上也能看出这个方法有多残暴...

(*怎么可以这么暴力的说*)  \[Pi]/2 Exp[NIntegrate[1/(\[Pi] x) ArcTan[((\[Pi] x+2)Log[(Sqrt[1-x^2]+1)/x]x)/(x^2Log[(Sqrt[1-x^2]+1)/x]^2-\[Pi] x-1)],{x,0,1},WorkingPrecision->50]]  ArcCot[1+1/(2\[Pi] ) NIntegrate[Log[((1-x^2)Pi^2+4(Sqrt[1-x^2]ArcTanh[x]+x)^2)/((1-x^2)Pi^2+4(Sqrt[1-x^2]ArcTanh[x]-x)^2)],{x,0,1},WorkingPrecision->50]]    > 0.73908513321516064165531208767387340401341175890075746496567242428255184768807`50.12267193056545  > 0.73908513321516064165531208767387340401341175890075746496567993239614795659229`51.22422170141253

参考书目

On Taylor series and Kapteyn series of the first and second type
Kepler's equation, radiation problems and Meissel's expansion
An exact analytical solution of Kepler's Equation

题图: https://www.pixiv.net/member_illust.php?mode=medium&illust_id=65616708

来源：知乎 www.zhihu.com
作者：酱紫君

【知乎日报】千万用户的选择，做朋友圈里的新鲜事分享大牛。点击下载

邓永泉-仲裁每日一问No.36 | 法理对于仲裁胜诉有帮助吗？

邓永泉

裁判判-仲裁之友创始人

北京仲裁委员会/北京国际仲裁中心仲裁员

dengyongquan@caipanpan.com

微信号：DENNISDYQ

问：法理对于仲裁胜诉有帮助吗？

答：非常有帮助。

首先，法理是一个完整的体系，它可以帮助当事人在不同层面、从不同角度完整、系统地阅读案件。

例如，买卖双方约定了具体的交货时间，但卖方为了节省运费，搭运货物提前向买方交货。卖方事先通知买方要提前交货，但买方收到通知后没有回复，待货物运到时买方拒绝收货，给卖方造成损失，卖方提起仲裁要求买方赔偿损失。

买方认为，双方约定了具体的交货时间，卖方提前交货，买方就有权拒绝收货。卖方认为，它此前多次提前交货，都是事先通知买方，买方不回复，但都收货了；这说明双方已经形成交易习惯，此次买方拒绝收货，应承担赔偿责任。

在该案中，买方只看到了双方的约定，但却忽略了诚实信用原则。诚实信用原则是法定原则，无需双方约定，对双方就有约束力，双方在订立合同阶段、履行合同以及合同履行完毕的各个阶段都应遵守。如果买方人员完整掌握了法理体系并且养成运用法理体系考察案件的习惯，就不会忽略诚实信用原则对双方履约过程中权利义务的影响。

其次，法理可以引导当事人制订仲裁策略。

例如，法理中有系统的抗辩事由，包括权利障碍抗辩、权利消灭抗辩、抗辩权抗辩，被申请人可以循着这些现成的抗辩事由考察自己的案件，制订恰当的仲裁策略。

第三，法理可以帮助当事人全面、准确地表达自己的观点，避免歧义或遗漏。

例如，申请人请求解除合同，循着法理体系就可以全面说明其解除合同请求的各个要素，即解除的空间范围（解除那份合同或哪几份合同，是全部解除还是部分解除）、解除的时间范围（解除是否有溯及力及其溯及范围）、解除的生效时间等。

第四，法理可以帮助当事人定位争议焦点问题。

例如，当事人就合同条款含义发生争议，循着法理体系就可以很快给双方争议定位，即没有约定或约定不明、理解争议。

第五，相当比例的仲裁员是法律学者，他们都习惯于从法理角度考察案件，当事人循着法理体系可以更有效地与他们交流。

邓永泉：邓永泉-仲裁每日一问No.35 | 合同内容和合同名称不完全对应的情况下，仲裁庭如何认定当事人的权利义务？

来源：知乎 www.zhihu.com
作者：邓永泉

【知乎日报】千万用户的选择，做朋友圈里的新鲜事分享大牛。点击下载

《法学方法论》读书笔记4.1作为案件及作为陈述的案件事实-1

刚刚准备把这篇读书笔记发上来的时候，发现上一篇已经是半年前的事情了。这半年，工作之外的时间基本上都在翻译书（18万字，已经交稿给出版社了），我也入了欧陆风云的坑，在知乎就是潜潜水。此后一段时间会多些一些读书笔记，当然，也会看心情多回答一些问题。
在第三章中，关于小前提部分的体量限于过于单薄，因为这部分的内容，在该书中单独作为一章来阐述，即作为案件及作为陈述的案件事实。
法律要适用于案件事实，才能发挥其作用。案件在事实上发生的情况，被称作"作为事件的案件事实（有观点将之称为"客观事实"）"，比如，原告为了要回为被告所伤而支出的医药费，其在诉状上将其和被告之间纠纷发生所有阶段的所有细节均描述的十分详细。但是，原告所陈述的这些案件事实，并非都会出现在判决书中，尤其是在判决书中"经审理查明"之后的部分，我们把判决书中"经审理查明"部分的事实，称作"作为陈述的案件事实（有观点将之称为"法律事实"）"。
我们在前面说过，就如同我们在后面依然会提到的那样，法官总是在做一种判断的工作，但这种判断并非仅仅在面对"作为陈述的案件事实"之时方才开始。在法官接触到一个新的案件的时候，呈现给他的往往是"作为事件的案件事实"的陈述，甚至只有前种事实的支离破碎的片段，而这种情形在原告没有律师作为代理人的情况下，会显得尤其糟糕。首先，需要考量已知的事实，这离不开原被告的陈述及其提交的证据，但这更多的是民事诉讼法中证据法的问题，如证明力、证明标准以及举证责任的分配等，在此，我们不多阐述，仅仅是将已经经过质证之后法官能够认定的事实作为考量的对象。其次，还要持续地对所有事实在法律上的重要性进行判断。在劳动争议案件中，劳动者可能会将入职到辞职之间的所有时间都陈述一遍，比如和同事关系如何、感谢某些师傅的带教等，但对于要求用人单位支付违法解除劳动合同赔偿金的案件而言，重要的法律事实主要在于入职和离职的时间（计算赔偿金的数额）以及用人单位解除劳动合同的理由和程序是否合法（是否应当支付经济赔偿金）。如此，才能形成"作为陈述的案件事实"。所以法官的法律判断在形成案件事实的阶段，即已经开始。所以，法官在撰写判决书的时候，眼光总是在"经审理查明"和"本院认为"部分之间来回往返。
恩吉施将确定小前提的划分为三个阶段：
第一，具体的生活事实，即对于实际上已经发生的案件事实的想象，也就是我们所说的"作为事件的案件事实"。
第二，确认前述事实，即前面所言的证据法的过程。
第三，判断案件事实是否具备法条的构成要件所要求的要素。
但是由于法官在形成案件事实的过程中就得考量特定的事实在法律评价上的重要性，所以，判断案件事实是否符合法律规定的构成要件，并不是在形成案件事实之后，一般都是同时进行的。但这两个阶段的区分并非是没有意义的，虽然这两个过程有所交织，但具体的工作依然是可以分离的，形成案件事实最终反映在判决书"经审理查明"部分，判断案件事实是否符合法律构成要件最终反映在判决书"本院认为"部分，前者所用到的是证据法的规则，通常用到的主观和客观的举证责任分配，而后者则是涵摄的过程，即考察在前述部分查明的事实是否和法律规定的构成要件相契合。
法律判断多以"未经加工的案件事实"作为起点，其大多以当事人的讲述为基本形式。这些讲述中会包含一些对于最终的法律判断没有意义的部分，法官在作出最终判断之前就会将这些无关紧要的部分剔除出去。比如，在劳动者以用人单位解除劳动合同未通知工会为由主张经济赔偿金的案件中，劳动者可能会讲到其在工作期间是多么的努力，其和公司管理层的交情是多么的号，但其陈述的这些事实和用人单位有无通知工会的最终判断毫无关系，不是作为陈述的案件事实。甚至，当事人在开庭之时陈述讲述这些事情的时候，法官也会提醒不要继续陈述以把控庭审节奏。就算是同样的事实，在不同的案件中的法律上的重要性也不甚相同。比如，同样是讲述劳动者什么时候开始跟着带教师傅的、其关系如何，在要求用人单位支付违法解除劳动合同经济赔偿金的案件中就不那么重要，但如果该案件是要求确认劳动者和用人单位之间存在劳动关系，劳动者所讲述的前述事实以及该带教师傅是否和用人单位之间存在劳动关系就十分重要。
法官应当追问所有的和作出最终判断相关的事实，即便当事人没有主动提及，以此来补充完整未经加工的案件事实，让最终"最为陈述的案件事实"包含在法律适用的判断上有意义的全部案件事实。比如，《劳动合同法》《工会法》中关于用人单位单方解除劳动合同应当通知工会的规定属于强制性规定，即便当事人没有以之作为诉请的事实，法官在庭审之中依然应当询问用人单位是否通知了工会以及通知的时间是否在一审起诉之前。而法官主动查明的这些事实无疑会出现在"经审理查明"的部分，所以，"作为陈述的案件事实"是思想加工处理后的结果，其中已经包含了法律的判断。在这个过程中，个别的事实已经运用特定的词汇来表达，这些词汇（比如陈某是2012年进入甲公司的）已经可以轻而易举的涵摄到法律概念（用工之日）之下。同时，陈述案件事实的语句也会描述一些模糊的、暗示性的东西。比如，甲驾驶乙的车辆撞伤了丙，并要求甲和乙共同赔偿其损失，原因在于甲是驾驶人，而其开的是乙的车。这里丙所谓的"乙的车"，并据此要求乙承担赔偿责任，很容易让我们联想到《侵权责任法》第49条和《道路交通事故案件解释》第1条规定的"有过错的机动车所有人"的概念，但该案中的乙究竟是否确系如此，就是一个法律判断问题，但是作出该法律的判断，尚得依赖补充查明其他的事实，比如，乙是否明知车辆存在缺陷、驾驶人无驾驶资格或者处于饮酒、吸毒的状态等。所有经过法律判断的事实都有类似的结构，都不仅仅是单纯事实的陈述，而是基于对其法律上重要性的考量，对事实所作的选择、解释和连接的结果。
但是，应当依据什么观点来选择"作为陈述的案件事实"应当包含的事实呢？

来源：知乎 www.zhihu.com
作者：棠邑小廌

【知乎日报】千万用户的选择，做朋友圈里的新鲜事分享大牛。点击下载

“贩卖焦虑”的时代，如何过好不用追赶别人的一生 | 心理咨询视角看“毒鸡汤”

这是最坏的时代，也是最好的时代。
我们这代人，被焦虑追逐，
又在焦虑中清醒。

随着最近韩寒发文怼《摩拜创始人套现15亿：你的同龄人正在抛弃你》及原作者回应，"焦虑"这个词又一次被推到大众的视野当中。

韩寒用"贩卖焦虑"、"制造恐慌"这样的字眼来批判原作者，同时提出自己的观点：

成功的定义是多样的，时代里不同人有不同的分工和命运，也有各自不同的幸福。安于现状或不甘如此都是每个人自己的内心意愿，他人不可强求。

喝不下原文作者"再不努力，你的同龄人，正在无声无息的抛弃你"的毒鸡汤的人为韩寒拍手叫好，可不要忘记，作为有10W+阅读量的这篇文章，"贩卖焦虑"是大有人买单的。

今天这篇文章，带你从心理学和心理咨询的角度来谈谈为什么总有人为"贩卖焦虑"买单以及如何在"贩卖焦虑"时代，过好不用追赶别人的一生。

以下内容整理自「心理咨询基础课程」阶课程中《人本主义相关学派理论和技术》、《认知行为理论和技术》和高阶课程中《焦虑议题的主要干预技术》的课程内容。

焦虑击中了我们内心共同的一根弦

为什么大家会为"贩卖焦虑"买单？

焦虑是共同的体验，
但并非所有的焦虑都是真实的

我们为焦虑买单，是因为焦虑引发了共同的体验。心理咨询认为：焦虑是一种正常的人类反应。（ps：此处所指的焦虑区别于临床上的焦虑障碍，指普遍的焦虑情绪）

人类普遍存在以下几种与焦虑有关的体验：

分离/失去：

无论是人际上的分离还是物质上的失去都会给人带来焦虑。

经典精神分析和客体关系理论均把与重要他人（比如母亲）之间的分离看作是重大的焦虑来源。

而现代心理学家丹尼尔卡尼曼也发现，人们对损失存在着天生的恐惧，为了避免损失或挽回损失，人们甘冒风险。

孤独：

人本主义心理学家罗洛梅指出，人类通过与他人建立联系获得成为自己的最初体验的，当无人陪伴时，会因为害怕失去这种成为自身的体验而焦虑，被社会接受、被他人喜欢之所以有这么大的力量，是因为可以阻止孤独的靠近。

死亡：

人类是所有动物中能够清楚意识到自己会死亡的生物，存在主义认为对于死亡的焦虑是人的普遍焦虑。

不确定性：

不确定性会让我们有一种不安全感。存在主义认为，对当前、对未来的不确定性是引发焦虑、阻碍幸福的原因之一。

"贩卖焦虑"的陷阱，并非所有的焦虑都是真实的。真实的焦虑是面对真实压力或危险时，产生的一些诸如担心、害怕、坐立不安的体验。但是，但我们每天面对的则更多是人为的"虚幻"的焦虑。

1.本我与自我的冲突："别人眼中的成功"还是"自己心中的舒坦"

精神分析-动力学认为：自我没法调节本我和超我之间的关系时，这种矛盾感引发焦虑体验。超我的标准主要来自父母和社会标准，比如高考选专业时"好找工作"vs"感兴趣"，毕业后找工作"名企高薪"vs" 真的喜欢"……

2.被强化的焦虑：年薪30W以下的人在北上广活得下去么？

社会学习理论认为，指个体在环境的影响下，即使在没有威胁的情况下，也呈现一定程度的焦虑。比如：社交媒体通过反复渲染"90后CEO一年收入100万"、"年薪30W以下在北京活不下去"等极端案例让打算一步一个脚印做下去的年轻人胆战心惊。

3.非理性认知：30岁没结婚会孤独终老么？

认知行为理论（CBT）认为，认知扭曲、非理性思考也可能产生焦虑。比如周围人、社交媒体传达的"30岁的女人没人要、比如你的身材体现你的阶层……更是让许多女性陷入自我怀疑的怪圈。

焦虑，能让人成功么？

看清焦虑的正反面

焦虑可以是动力，也可能压得你无力喘息。

心理动力学派和存在主义的部分理论将焦虑视为一种成长的动力。中年危机、社会孤立、死亡焦虑都有它有价值的部分。

比如荣格认为中年危机能让一个人有机会去整合内外资源，成为一个真正像自己的人。人到中年很多责任完成到一定程度，可以把注意力回到自己身上，当个体意识到自己好像从没有为自己而活的时候，焦虑的感觉浮现，这种危机感也就油然而生。

（点击阅读：有些人中年危机，有些人开始做自己）

阿德勒认为社会孤立的焦虑感能让个体发挥更多的社会兴趣，投入到更多的社会关系当中，成为一个对关系投入的人。比如很多体验或学习心理咨询的同学都是因为自己的重要社会关系上遇到一些问题，促使他们学习和发生改变。从这种意义上讲，焦虑可以成为转变的契机。

存在主义视焦虑为一种生存的状态使人为生活负责等。因为死亡是必然的，因为死亡的不可避免引发的存在焦虑，能够让个体意识到需要把握好自己有限地实践去做对个体而言真正有意义的事情，比如有些人在生病或者从意外中获救之后放弃追逐事业去陪伴家人或者是帮助别人，通过这种方式创造存在的意义和价值。

然而，并不是所有的焦虑都会转化为动力，持续地暴露在压力或者焦虑的环境中不仅无助于成功，更会损害个体身心健康。

Hans Selye 是一位医生，发现虽然他的门诊病人都处于长时间压力之下，但是一部分人能够在压力当中如鱼得水、自得其乐，展现相当多的才能；而另一部分人则在压力之下出现一种无力感，疲惫不堪的反应。

如果长期暴露在持续焦虑或者越来越重的焦虑中，人会有耗竭感，也就是我们常说的"身体被掏空"的感觉。这可能使人放弃努力，也有可能使人出现临床上的焦虑症，产生失眠、头疼、胃痛等身心症状。

"贩卖焦虑"的时代

如何过好不用追赶别人的一生

在这个不断制造、贩卖焦虑的环境中，别人家的孩子、创业成功、年薪30w以上……都只是少数，而且光环背后，无论是普通人还是所谓的成功人士，都有自己的焦虑，追赶别人是一条没有尽头也没有出口的路。

对每个人来说，如何过好不用追赶别人的一生呢？简老师从课程中为大家总结出以下几条建议：

1.探索焦虑的背后的冲突，去做真实的自己。

弗洛伊德创始的精神分析治疗鼓励个体有能力去体验焦虑，使焦虑作为一种讯号去探讨产生焦虑的内在冲突，一旦内在冲突得到解决，个体的焦虑感便会消失。

是"大城市的一张床还是小城市的一套房"，本身都没有对错，与其日日焦虑，不同弄清背后的原因，做真实的自己。

存在主义认为，自我觉察（self awareness）是生命的基石，我们要寻找的是自己定义的自己，而不是总是看别人会怎么允许自己、评判自己。相信自主自尊是来自我们自己的，而不是别人对我们的期待。

自我觉察的过程可以借助心理咨询或者咨询的学习在专业人士的指导下进行。

2.尊重个体差异、建立健康的人际关系

后精神分析学派代表霍妮认为焦虑是一种"在充满敌意的世界，一种慢慢增加、广泛渗透的寂寞与无助"。哈佛大学持续75年的追踪研究发现，决定我们幸福的是健康的人际关系而非名誉、金钱、社会地位这些所谓的成功标准。

还记得高考时千军万马过独木桥么？成绩好的学生暗中较劲，如果成功的标准和考试一样单一，那么人和人之前的交往也会带有敌意，紧张的人际关系会加重孤独所带来的焦虑和无助。

这个世界并不是非黑即白的，人也远不只能用成功或者失败来划分，每个人来到这个世界上，都带有自己独特的天赋和能力。当我们以开放的心态来看待人与人之间的差异时，成功的内涵就会变的丰富，当我们能够接受自己的真实存在时，人际关系也能变的真实。

3.开放视野、积极打破不合理信念

认知行为疗法（CBT）认为我们之所以焦虑、痛苦是因为存在引发这些情绪的非理性、不合理的信念。比如说很多姑娘明明不胖却因为体重焦虑是因为她们认为"好女不过百"，而很多人也会因为"30岁还没有做到管理层就没前途了"的观念而忧心忡忡。

如果我们仔细观察、深入了解，不难发现过了100斤的好姑娘大有人在，没做到管理层的人可以很成功，谎言说了一百遍就会成真，生活中我们仍然不免受到这些不合理信念的影响。

对于这些不合理信念，认知行为疗法会通过认知重建的方式，通过识别这些影响我们的潜藏信念、发现它们的不合理之处、修正它们来缓解、治疗焦虑。

其实对于我们每个人来说，当外界传达给我们这些观念时，问一下"这个观点是真的么？"、"这个观点合理么？""这个观点能代表所有人么？"当你把视野打开，不再受限于那一两个极端，你就会发现很多让你焦虑的观点是那么可笑。

4.活在当下，只有当下才是最真实的

人本主义认为，焦虑是对当前发生的事情和今后要发生的事情的一种不确定性的恐惧。通过自我觉察来关注当下能帮助我们摆脱焦虑。

5.承担自由和选择的责任，勇敢地选择自己的生活，也是一种成功。

存在主义认为自由和选择的冲突也是焦虑的来源，我们之所以会被外界的观念影响那么多，是因为我们害怕做出选择和承担选择的后果。

正如存在主义所说的，对于每个人来说生命都只有一次，能够承担和设计当下的生活的只有你自己。

原文发表于："贩卖焦虑"的时代，如何过好不用追赶别人的一生 | 心理咨询视角看"毒鸡汤"

学心理咨询，到简单心理Uni： 简单心理Uni - 最有态度的心理咨询学习社群

我们还有公众号哟~ 关注简单心理Uni (微信号：jdxl-uni) ，行业大咖的免费课程、专业咨询文章、读书会、专题课程，与10万+成长中的咨询师一起学习一起飞！

「简单心理Uni金牌基础训练课程·2018年秋季班」正在招募中～2年，理论、实习、督导缺一不可的系统培训，和你一起成为可靠的咨询师！

来源：知乎 www.zhihu.com
作者：简单心理Uni

【知乎日报】千万用户的选择，做朋友圈里的新鲜事分享大牛。点击下载

订阅：博文 (Atom)