经典网文分享

统计力学Ⅱ——1.集体行为，从粒子到场

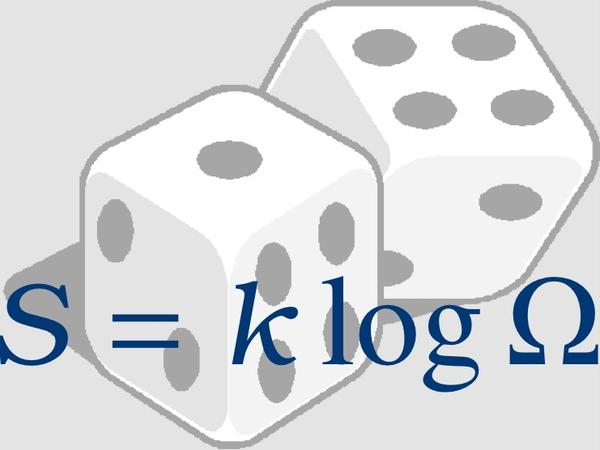
I. A 引言

这一部分的目的是介绍统计力学原理，它为微观物理学的基本定律和宏观尺度下的观测现象提供了桥梁。

微观物理学的特征是含有大量的自由度：例如，一团气体中粒子的位置和动量 $(q_i,p_i)$ ，磁体的自旋构型{ $\sigma _i$ }，或正则系综的占有数{ni}。这些自由度的演化是由基本的哈密顿量 H 所控制。

宏观物理学通常由一些平衡态变量来描述，例如压强P，体积V，温度T，热能E，熵S，等等，它们服从热力学定律。

统计力学提供了两个领域之间的概率连接。例如，在一个温度T的正则系综中，系统的每一个微观状态都对应概率 $p(i) =e^{ -\beta H(i) }/Z$ ，其中 $\beta= 1/(k_BT)$ 。总概率是归一化的，配分函数Z(T)必须等于 $Z=\sum _i e^{ -\beta H(i) }$ 。然后从自由能 $F = k_BT lnZ$ 中提取出系统的宏观状态的热力学信息。

上述程序实际上只适用于有限数量的简单系统，大部分描述的是粒子的非相互作用集合，其中的配分函数可以精确计算。一些相互作用效应可以使用精确求解的微扰法处理。然而，即使对于非理想气体的相对简单的情况，微扰法也会在凝结点附近失效。另一方面，正是由于相互作用而产生的大量的新相和特性使宏观物理学变得有趣。特别是，我们希望解决以下问题:

在热力学极限(N→∞)下，强的相互作用导致新相。我们研究了一些细节上最简单的液体-气体转变的例子，但实际上还有许多其他有趣的相，如固体，液晶，磁体，超导体等。从粒子的相互作用到体系的宏观行为，将如何描述？描述这些相的宏观热力学量是什么?
系统特有的低能量激发是什么?在固体或超流体氦的声子情况下，低能激发是典型的集体模式，包括许多微观自由度(粒子)的协调运动。这些模式很容易受到热扰动的影响，并通过散射实验来探测。

粒子间相互作用的微观哈密顿量通常是相当复杂的，这使得对问题的初始粒子处理方法变得棘手。然而，在许多这样的系统中，它们的宏观行为有许多共同特征，这些特征仍然可以通过统计力学的方法得到有效研究。尽管在微观尺度上，粒子之间的相互作用是非常不同的，人们可能希望，对足够多的粒子进行平均，会得到更简洁的描述。(在同样的意义上，中心极限定理保证了许多随机变量的和是简单的高斯分布。)在许多情况下，这种期望确实是合理的，因为在长波长和长时间内，相互作用系统的集体行为变得更加简单。(这有时被称为流体动力学极限，通过类比于流体的粒子 Navier-Stokes 方程。)与这些长度和时间尺度相适应的平均变量不再是粒子自由度的离散集合，而是缓慢变化的连续场。例如，在Navier-Stokes方程中出现的速度场与流体中单个粒子的速度是完全不同的。因此，在交互系统中研究集体行为的有效方法是场的统计力学。

我们的目的是

•目标：学习描述和分类物质的状态，它们的集体属性，以及从一个相到另一个相的转换机制。

•工具：经典场论的方法;使用对称，微扰理论，以及重正化群(RG)方法处理非线性问题。

I. B 声子和弹性

弹性理论是场论中最简单的例子之一。我们将证明弹性介质的某些性质是如何得到的，无论是从第一原理开始的复杂方法，还是用更简单的对称性方法来研究问题。因此，它代表了从现象学方法中可以学到多少东西的一个原型。计算固体低温热容的问题可以用从头算和现象学方法来研究。

(i)从头算(粒子)方法:从第一原理计算固体材料的热容是相当复杂的。我们简要介绍一些步骤：

•从头算的起点是关于电子和离子的薛定谔方程，只能用密度泛函形式来表示。相反，我们从一个多体势开始，为离子坐标 $V(\vec q_1， \vec q_2，,,, ， \vec q_N)$ ，这本身就是量子力学处理的结果。

•在零温的理想晶格位置是通过最小化V来实现的，通常形成一个晶格 $\vec q(ℓ,m,n)=(ℓa+ mb + nc]≡\vec q^∗_r$ ，其中 r = {ℓ,m,n }是一个三元组整数,,a,b,c是单位向量。

•设定 $\vec q_\vec r = \vec q^*_\vec r + \vec u(\vec r)$ 时，理想位置的小波动(由于温度或量子效应)。引起势能
的变化量为

$V= V^*+ 1/2\sum _{r,r',\alpha,\beta } \frac {\partial^2V}{\partial q_{r,\alpha }\partial q_{r',\beta }} u_\alpha (r) u_\beta(r') + O(u 3 V) \\$ 1.1

(V的一阶导数在平衡位置为0)微小位移下完整哈密顿量，只需将动能项 $\sum _{r,\alpha} p_\alpha (r)^2/2m$ 加到eq.(I.1)。

•下一步是通过对角化导数矩阵找到振动(声子)的简正模式。由于基态构型是规则格子，所以这些矩阵元必须满足平移和旋转对称性。例如，它们只能依赖于离子的位置向量 r 和 r' 的位置向量差，即

$\frac {\partial^2V}{\partial q_{r,\alpha }\partial q_{r',\beta }} =K_{\alpha ,\beta}(\vec r -\vec r') \\$ 1.2

平移对称使得我们至少可以用傅里叶变换对汉密尔顿函数进行部分对角化，

$u_\alpha (r)=\sum _\vec k ^l\frac{e^{ikr}}{\sqrt{N}} u_\alpha (\vec k)\\$ 1.3

(只有第一个布里渊区内的波矢量k对求和有贡献。)哈密顿量为

$H=V^*+ 1/2\sum _{k,\alpha \beta }[ |p (~ k)| ^2 /m+K_{\alpha ,\beta} (\vec k) u_\alpha (\vec k)u_\beta (\vec k)^*]\\$ 1.4

而傅里叶变换矩阵的精确形式 $K_{αβ}(\vec k)$ 是由微观相互作用决定的，它必须遵从底层晶体点群的对称性。我们假设，对角化3*3矩阵特征值 ${\kappa _\alpha (k)}$ ，哈密顿量的二次部分现在分解为一组独立的(非相互作用的)谐振子。

•最后一步对每一个谐振子量子化,得到

$H = V^∗+\sum _{k,\alpha}hω_{α}(\vec k) (n_α(~ k)+ 1/2 )\\$ 1.5

其中 $ω_{α}(\vec k)=\sqrt{κ_α(\vec k)/ m}$ 、{ ${ n_α(\vec k)}$ }是占有数集合。

温度T下的平均能量为

$E(T)= V^∗+ \sum _{k,\alpha} hω_α(\vec k)(<n_α(\vec k)>+ 1/2),\\$ I.6

我们从统计力学基础知道平均占有数是由 $n_α(\vec k)= 1 /[ exp(\hbar \omega /k_BT)−1]$ 给出。显然，E(T)和其他宏观函数有复杂的行为，依赖于 ${\kappa _\alpha (k)}$ 的微观细节。这些函数有什么特征(例如，T 趋于0的函数依赖)，独立于微观特征吗?

以一维线性链来说明

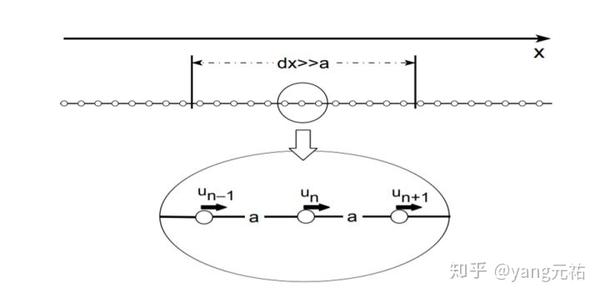
I.1一维链的位移和粗粒化

考虑一维粒子链，被限制在一维运动。粒子链的势能可表示为

$V = V^* + K_1 /2 \sum_n (u_{n+1}-u_n)^ 2 + K_2 /2 \sum_n (u_{n+2}-u_n)^ 2 +··.\\$ I.7

分解简正模式得到

$u_n=\int_{-\pi/a}^{-\pi/a} dk/2\pi *e^{−ikna} u(k),其中u(k)=a\sum_n e^{ ikna }u_n$ I.8

(注意eq. (I.3)的归一化的差异。)由此得到势能为

$∗V = V^* + K_1 /2 \sum_n \int_{-\pi/a}^{-\pi/a}dk/2\pi dk'/2\pi (e^{ika}-1)(e^{ik'a}-1) e^{-i(k+k')na} u(k)(k′) .\\$ I.9

使用 $\sum _n e^{-i(k + k′)na} =δ(k + k′)2π/ a$ ,并且 $u(−k)= u^∗(k)$ ,我们得到

$V = V^* + K_1 /2a \int_{-\pi/a}^{-\pi/a}dk/2\pi [K_1(2-2cos2ka) K_2(2-2cos2ka)+...] |u(k)|^2 .\\$ 1.10

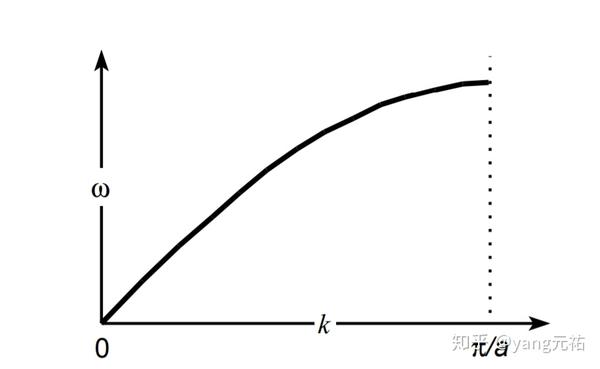
简正模式的振动频率由 $\omega(k) =\sqrt{[2K_1(1-cos2ka) +...]/m}$ 给出

如下图所示。在k趋于0的极限下， $\omega(k)趋于|k|*v$ "声速"v等于 $\sqrt{\bar K /m}$ 。

对于一维N粒子链，这些激发态的内能为

$V = V^* + Na \int_{-\pi/a}^{-\pi/a}dk/2\pi \frac{\hbar \omega(k)}{e^{\hbar \omega(k)/k_BT}-1} .\\$ I.11

当T趋于0时，只有h (k) < kBT的模式是激发态。因此，只有激发谱 k→0 部分是重要的，E(T)化简为

$V = V^* + Na \int_{-\pi/a}^{-\pi/a}dk/2\pi \frac{\hbar v|k|}{e^{\hbar v|k|/k_BT}-1} = V^* + Na \frac{\pi ^2}{6\hbar v}(k_BT)^2.\\$ I.12

注:

(1)激发能的全谱为

$K(k)/2= K1(1−cos ka)+K2(1−cos2 ka)+ ···⇒Kk^2/2... k→0\\$ I.13

进一步近邻相互作用将改变声速，而不再是 k→0 时的色散关系。

(2)热容C(T) = dE/dT与T成正比，这具有普适性，即非物质特性，且与原子间相互作用的选择无关。

(3)能量的T^2依赖性源于k→ 0(或波长区域无穷大)的激发，即包含大量粒子的集体模式。这正是统计考虑有意义的模式。

(ii)唯像法：我们现在概述了同一问题的介观方法，很容易推广到高维。在低温条件下，典型激发态的波长为 $\lambda>\lambda (T)\approx (hv/kT) \gg a$ ，其中a为晶格间距。我们可以通过称为粗粒化的平均过程来消除不重要的短波模式。这个想法是考虑在一个点，一个间隔 a≪dx≪λ(T) 周围内(图I.1)。在 dx 中所有的位移 u 都近似相等，我们可以定义一个平均形变场 u(x) 。动能与密度有关 $ρ = m/a ....由... ρ \int dx \dot u^2(x)/2.$ ，u(x)被视为一个连续函数，但它不会比晶格间距 a 更小。

对于一维链来说，最一般的势能函数V[u]是什么?我们不太了解的形式V(u),但我们可以使用一般原则来构建：

位置：在大多数情况下,粒子之间的相互作用是短程的，我们定义在点 x 的势能密度Φ， $V[u]=\int dxΦ( u(x),du/dx,...)$ 。当然，通过包括所有的导数，我们也可以描述长时间的相互作用。在这种情况下，"局域性"一词意味着较高的导数项不那么显著。

平移对称：链的均匀平移不改变其内能，因此能量密度必须满足约束条件 $Φ[u(x)+c]= Φu(x)$ 。这意味着 Φ 不直接依赖于u(x)，而只依赖于其导数 $du/dx, d^2u/dx^2$

稳定性：由于波动是围绕平衡解的，所以在u或它的导数中没有线性项。(稳定性进一步要求V[u]的二次项必须是正的。)

与这些约束相一致的最普遍的可能性是。

$V[u]=\int dx[K/2 \frac {∂u}{∂x}+ L/2(\frac {∂u}{∂x})^2 + ...+M (\frac {∂u}{∂x})^3+...]\\$ I.14

经过傅里叶变换

$V[u]=\int dk/2\pi [\frac {K}{2} k^2+ \frac {L}{2} k^4 + ...+...]u^2(k) \\-iM\int \frac { dk1}{2\pi} \frac {dk2}{2\pi} k1k2(k1 +k2)u(k1)u(k2)u(−k1 −k2)+.\\$ I.15

k→ 0时，高阶梯度项(如L)变得不重要。此外，对于小变形，我们可忽略 u(如M) 的二阶项，加上动能，我们得到了一个简单的一维场理论，哈密顿量为

$H=\frac{\rho}{2}\int [(\frac{\partial u}{\partial t})^2+v^2(\frac{\partial u}{\partial x})^2]dx \\$ 1.16

这是一维弹性(弦)理论，与物质相关的常数 $\rho$ ，和 $v = \sqrt {K/\rho}$ 。虽然唯像方法不能告诉我们这些参数的值，但它确表明，低能激发能满足 $\omega =v|k|$ 的色散关系。

我们现在可以将弦的弹性理论推广到任意维d：离散粒子变形 $\vec u_n$ 粗粒化到一个连续变形场 $\vec u(\vec x)$ 。对于各向同性材料，势能V[~u]，在转动和平移下都必须是不变的，而 $u_α(\vec x) → R_{αβ}u_β(~x)+ c_α,$ R是一个旋转矩阵。局部量对称应变场为

$u_{α\beta}(\vec x)=\frac{1}{2}[\frac{\partial u_α}{\partial x_\beta}+\frac{\partial u_\beta}{\partial x_α}]dx \\$ 1.17

对重复的指标求和可以保证结果是旋转不变的。

$H=\sum _{\alpha,\beta}\int [\frac{\rho}{2}\frac{\partial u_\alpha}{\partial t}+\frac {2\mu}{2}u_{\alpha,\beta u_{\alpha,\beta}}+\frac {2\lambda}{2}u_{\alpha,\alpha u_{\beta,\beta}}] d^d\vec x\\$ 1.18

这个旋转不变性在傅里叶基底中是更清晰的，

$u(\vec k)=\int e^{i\vec k.\vec x}\vec u(\vec x)d^d \vec x$

$H=\sum _{\alpha,\beta}\int [\frac{\rho}{2}|\dot u(\vec k)|^2+\frac {\mu}{2}k^2|u(\vec k)|^2+\frac {\mu +\lambda}{2}(\vec k,u(\vec k))^2] \frac{d^dk}{(2\pi)^d}\\$ 1.19

显然只包含旋转不变量 $\vec k ·\vec k， \vec u ·\vec u，和\vec k · \vec u$ 。

进一步将哈密顿分解为两种类型的声学模式:

纵向模式 $v_ℓ=\sqrt{(2µ+λ)/ρ}$ ,和横向模式 $v_ℓ=\sqrt{µ/ρ}$

可以得到内能为

$E(t)=L^d\int \frac{d^dk}{(2\pi)^d} [\frac{\hbar v_l k}{exp(\hbar v_lk / k_BT)-1}+\frac{(d-1)\hbar v_t k}{exp(\hbar v_t k / k_BT)-1}]≈A(vℓ,vt)L^d(kBT)^{d+1}\\$ 1.20

热容 $T →0， C ∝T^d$ 趋于0.

注:

(1)所有与物质相关的参数均包含在A中。
(2)普适指数源于(流体动力学) k→0 的模式。高频(短波波长)模式只在高温下出现。
(3)比例指数取决于维度和相互作用范围。(长程库仑相互作用将导致不同的结果。)

还有许多著名的例子证实了能量法则的普适性和重要性。例如，考虑一团示踪剂在某种未指明的介质中移动。随着时间t演化，某些特征标度x使我们能够了解粒子运动的动力学

(1)扩散，在这种情况下， $x∝\sqrt{Dt}$ 。

(2)耗散输运, $x∝vt$ 。

(3)均匀力场运动，如引力场 $x∝gt^2/2$ 。流体动力学 Navier-Stokes 方程是另一个例子。我们可以用这些例子来构建和分析唯像理论。

一般步骤:

(1)粗粒化哈密顿量，输入来自对称性、相互作用域和维数等参数。
(2)与上述例子不同的是，在有效场论中，一般非线性不能被忽略。我们将学习如何用微扰理论和重整化群的方法来处理非线性问题。
(3)分析输出用通用指数表示，其他函数依赖可以直接与实验进行比较。

来源：知乎 www.zhihu.com
作者：yang元祐

【知乎日报】千万用户的选择，做朋友圈里的新鲜事分享大牛。点击下载

空姐打滴滴遇害案的七个法律问题

本文作者：中闻律师事务所合伙人赵虎律师

空姐打滴滴遇害案发生之后，很多人关注其中涉及到的法律问题，比如滴滴应付负责，顺风车与网约车有区别吗？我们总结了这些大家关心的问题，从法律进行解答。

1、犯罪嫌疑人已经死亡，是否意味着这个案件已经结束了？

这个案件是一个刑事案件，公安机关已经立案侦查。作为刑事案件来讲，如果犯罪嫌疑人已经死亡的情况下，案件就终结了。

另外，虽然犯罪嫌疑人死亡，但是这个案件又是一个侵权案件，侵犯了他人的生命健康权，可以另外起诉对方或相关责任人侵权，这就是一个民事案件了。

2、如果主张赔偿，那么起诉的主体是谁呢？

原告对于起诉的主体有选择权，因此主体有这么几种可能性：

第一，犯罪嫌疑人没有去世的前提下，他肯定是第一被告；

第二，犯罪嫌疑人死亡的情况下，这里面可能涉及到——滴滴公司。滴滴公司要不要承担侵权责任。在这个案件过程中，滴滴公司是不是起到一个帮助侵权的一种作用。如果起到了帮助侵权的作用，就要承担侵权责任。关于这一点，滴滴公司本身也声明了其要承担相应的责任。

第三，车辆在犯罪嫌疑人父亲的名下，他的父亲也可能需要承担法律责任。

3. 网约车有很多种：正规的出租车、快车、专车等，顺风车与其他的网约车有什么区别吗？

在国务院出台了《国务院办公厅关于深化改革推进出租汽车行业健康发展的指导意见》中，特意单独规定了顺风车，把顺风车与其他类型的网约车进行了分开说明，即"规范发展网约车和私人小客车合乘"。

根据《国务院办公厅关于深化改革推进出租汽车行业健康发展的指导意见》的规定：私人小客车合乘，也称为拼车、顺风车，是由合乘服务提供者事先发布出行信息，出行线路相同的人选择乘坐合乘服务提供者的小客车、分摊部分出行成本或免费互助的共享出行方式。私人小客车合乘有利于缓解交通拥堵和减少空气污染，城市人民政府应鼓励并规范其发展，制定相应规定，明确合乘服务提供者、合乘者及合乘信息服务平台等三方的权利和义务。

从这个指导意见的规定来看，首先拼车或者顺风车和其他的网约车的性质是不同的。它属于一种合乘的性质，并不是说以此来运营。我们知道，专车、快车等其实是网约车平台运营的车辆，属于运营性质。

另外，这个指导意见也提出了要求各城市人民政府应当出台相应的意见、规定，来规范顺风车的发展。

所以从这个情况下来看，顺风车在法律上与快车、专车等网约车还是有不同之处的。

4. 滴滴平台是否要负具体的责任？

滴滴平台是否要负责任，就要看它是否尽到法定的义务。有关法定的义务，各地的规定不一样。

先说下北京市的规定，北京市出台的《北京市私人小客车合乘出行指导意见》中，对于驾驶员应当具备什么资质进行了相关的规定。"驾驶员应有1年以上驾龄，身体健康；在合乘中应当依法自律、安全驾驶；所选择的线路应当符合顺路便行的原则。提供合乘的车辆须是驾驶员本人所有的、具有本市号牌且经检验合格的7座以下小客车。"

《指导意见》要求：车主注册要实行实名制，驾驶员身份证、驾驶证；车辆行驶证及保险状况等信息；合乘者身份证；驾驶员、合乘者的手机号码；不得为驾驶员和车辆条件不符合要求、登记事项不完备的合乘行为提供注册和合乘信息服务。驾驶员和车辆如发生违法行为或不符合相关条件的，合乘信息服务平台应当及时注销其注册信息、停止提供合乘信息服务。

《指导意见》已经出台，那么像滴滴这类的平台就有义务要履行。另外还规定了 "驾驶员提供合乘服务每车每日不超过2次。"，是有次数的限制，这点目前各个车辆合乘平台做的还不够好。

以上是北京市的规定，本案发生在郑州，郑州本地的意见并没有正式出台，仅有一个《征求意见稿》，但是还没有生效，仅供我们参考。其中也有一些与北京市相类似的规定。比如说关于司机的规定，要求必须在通勤时间，每日次数少于4次等。如果这个规定已经生效了，这个案件发生的时间就有问题，是在非通勤时间发生的。

从以上情况来看，滴滴公司还是要承担责任的，大概有以下几点：

第一，人车不合一。犯罪嫌疑人是使用其父亲的身份进行顺风车，滴滴也表示其人脸识别失效了，是有问题的。说明滴滴没有做到法律规定的要求。

第二，驾驶员曾经被投诉多次，平台并没有进行任何的处理，还让其继续进行顺风车。另外，这个人是专门进行顺风车的，成为一种运营手段，已经不是顺风车的概念了。滴滴让顺风车变成了可以营运的方式，是有问题的。

第三，是否为犯罪提供了帮助，比如说对信息的审核是否严格；对于乘客信息以及评价是不是必要的内容；是不是客观上为犯罪分子挑选犯罪对象时提供了相应的帮助等。

5. 很多人已经证实了在司机端可以看到乘车人的各种标签、描述等，是非常详尽的，暴露了个人信息。为什么要让司机端或者整个平台上看到个人信息，这样做会有哪些隐患问题？这一点会不会成为本案中所谓的"助推作用"呢？

首先，我们来看滴滴为什么设置这些信息，我们可以认为滴滴这样做是为了提供更好的服务，这些信息可以供双方进行了解，可能平台会有这方面的考虑。

其次，滴滴这种平台是不是应当对于评价的内容进行限制，哪些信息对于合乘来讲是有用的；哪些信息对于合乘来讲是没用的。

再次，这个平台要做的是信息平台还是社交平台？这些必须考虑清楚。如果要做社交平台就要根据社交平台的方式进行约束，提供的信息、要求都是不一样的。作为平台来讲，法律对于平台的要求也是不同的。如果提供的只是一个车辆服务的平台，而去做社交，那么造成他人的侵权行为需要承担法律责任。

社交平台可以任由用户全方面的评价一个人，只是作为一个信息平台，双方目的明确，只是合乘一辆车而已，这些信息有用吗？还要考虑到这些信息有害吗？

最后，从犯罪嫌疑人这边来讲，他想进行一个犯罪需要好几步。先有了犯罪的动机，动机之后要找合适的机会、合适的对象，当你提供这些信息的时候，是否给了犯罪分子提供了一个合适的对象？如果他是借助这样一个平台找到了合适的犯罪对象，这样情况下滴滴就为这些犯罪提供了帮助。所以本文认为从这一方面看，平台的后台信息没有进行筛选、限制，是存在问题的。

6.滴滴在案发后曾经发布过悬赏公告，顺风车司机的各种信息都在上面，非常清晰。这样一个悬赏行为有没有问题呢？

这也是有问题的。有的人戏称这为"发通缉令"，这个悬赏令已经具备了很多通缉令应有的因素。关于通缉令，法律有明确的规定：谁能发布；按照什么程序发布。

刚开始报案的时候我们只知道一个犯罪行为，慢慢的将几个人纳入怀疑的对象，最后确定一个对象，通过其他的证据掌握、确定犯罪嫌疑人。有了一定的证据之后，才可以申请发通缉令。

从法律上来看，只要一个人没有最终被定罪，我们都应当认为其只是有嫌疑，不能想当然的认为这个人是罪犯了。

现在，一个企业发布了类似于通缉令性质的悬赏公告。之前几乎没有发生过这种情况，或许之前也很少有企业有能力实现这一一个效果。我们也应当思考一下之前为什么很少出现这种情况，之后怎么办。相关的侦查机关也应当进行反思：对于这样的大型互联网平台，它们的能力越来越大，有没有权利和资格发布这类东西？它们发布这类东西应当经过什么程序？是否需要经过公安机关的批准？

7.网约车企业应当是否承担社会责任呢？

企业应该承担社会责任的，企业的社会责任这一点不仅是一句空话，在公司法中有规定。

企业越大，社会责任也就越大。

企业的作用狭义来看是自负盈亏的，为股东牟利。但是从广义上来看很多企业所提供的服务是我们必要的服务。比如说吃穿住行。在这个服务过程中需要很多其他匹配的条件，比如政府的规划帮助、用户的信息等。这一部分长期以来是由政府部门或者国有企业提供的，在市场慢慢放开以后，才有私营企业去做这种服务。一方面企业需要赚钱，另一方面企业也需要将相应的服务提供好，把用户信息保护好。

从这方面来看，这些企业如果不考虑自身的社会责任，不但在商业道德上存在问题，在法律上也是有问题的。

综上，空姐打滴滴遇害这一的事件其实是一个小概率事件，因此用户在用网约车平台打车方面不用太过于担心。

来源：知乎 www.zhihu.com
作者：中闻律师事务所

【知乎日报】千万用户的选择，做朋友圈里的新鲜事分享大牛。点击下载

《腐烂国度2》临时评测7.5分作为半价游戏，它挺靠谱

　　注：由于在正式发售前很难匹配到其他玩家，游戏的多人游玩部分我们尚未进行充分体验，因此本文只是针对《腐烂国度2》单人游玩部分的临时评价。考虑到线上功能是这部新作最重要的特性之一，我们会在游戏正式发售后进行全面体验，并尽快推出完整版评测。到时候我们对这款游戏的评价和评分可能会发生变动。

　　五年前的初代《腐烂国度》并没有革命性的创新，各方面机制也远远没有打磨得足够完善，但是依然通过一系列微创新精确地触到了一部分核心生存游戏爱好者的痛点。2013年的丧尸题材游戏市场已经是一片红海，但是一款将生存、城建、社区运营等元素有机融合起来，并且还提供了开放世界的游戏，在当时依然足以让人眼前一亮——更何况，这款游戏的售价还不到一款正常3A大作的一半。

　　如果继续以2013年的标准来衡量，最近发售的《腐烂国度2》恐怕就是这款游戏最理想的形态。它比初代作品更充实、更细致、加入了万众期待的多人联机系统，并且依然保持着极为诱人的低价。不过时过境迁，不论是游戏界的设计标准，还是玩家的需求，都跟五年前相比发生了微妙的变化。《腐烂国度2》的这些进化要想跑在时代和玩家审美前面，恐怕反而没有当年那么容易了。

末日求生

　　《腐烂国度2》的核心理念与基本玩法和前作一脉相承。本质上来说，它并不是一款以特定主角及其配套成长体系为聚焦点的游戏——你真正培养的（或者说运营的）是一个幸存者社区。在游戏过程中，你可以选择扮演任何一个角色，他们有着不同的专长、不同的背景故事、以及不同的性格。每个角色都有一套独立的成长体系，不过与此同时死亡也是不可逆转的。永远不要期待游戏中会有检查点帮你复活喜欢的角色。

　　这种设计最大的优势在于能够让你放眼宏观和大局，从社区或团队整体的角度去考虑生存这件事，并且在具体执行计划的时候，又能把任务具体落实到最合适的角色身上。比如你会为补充社区稀缺资源而有计划地探索各种各样潜在的资源点，主动清理威胁社区的丧尸群，或者与周边其他幸存者聚落展开贸易。你可以扮演擅长奔跑、射击、格斗的角色外出杀敌，通过有着贸易天赋的商人做生意，利用有着建造特长的工程师提高各种设施的建造效率……

　　当然，这种聚焦于整体社区的处理方式也有着非常明显的短板。整个游戏流程中基本上找不到稳定的叙事主体，游戏也因此很难打磨出精巧的故事。在不断切换角色的过程中，游戏很难让玩家在特定角色身上投入足够丰富的情感，更妄谈输出有深度的价值观。游戏中的任务数量虽然足够丰富，但是却基本上是零零散散的一盘散沙；其设计水准也基本上停留在"到某地、拿某物、杀某人"这种公式化的网游水平。随着游戏流程的逐步推进，游戏中后期的任务体验也变得越来越重复枯燥。

　　《腐烂国度2》中的人口既是最稀缺的资源，也是最沉重负担。一方面，社区的生存和发展离不开具备战斗、医学、种植、化学、电脑等知识的人才；但是另一方面，要在同一时间养活这么多人，又会大量消耗食物、药品、弹药、建筑材料等资源。而这其实也是驱动你不断拓展社区规模、改进资源获取效率的原动力。在生存状况极为凶险的时候，你可能不得不放逐多余的人口、威胁劫掠原本和善的邻居、甚至是处决在医疗站休养的感染病人来节省资源。

　　这款游戏在具体探索和战斗的部分则处理得相对传统和保守。丧尸对你造成的压力基本上是与对方的数量成正比的。单独的或者少数几个僵尸，不论其本身多么厉害，总是有比较广阔的回旋空间让你从容应对，而这也就让潜行和暗杀在很大程度上成为了探索过程中的最优解。在避免被僵尸群发现这个关键点上，游戏也引申出了许多既刺激又讨巧的小点子。行走、翻窗、破门、翻箱倒柜、汽车引擎、丧尸吼叫、燃放爆竹都可能会发出足以招来大批僵尸的噪音——这些声音除了能得体地营造紧张气氛之外，还给游戏的过程赋予了非常广阔的策略施展空间。如果能巧妙地利用声音操控僵尸的动向，游玩的过程将会如鱼得水。

　　除了成群结队的丧尸群之外，探索过程中压力的另一大来源则是极为严格的资源管理和状态数值控制。每个角色的血量和体力上限会随着疲劳、饥饿、受伤等异常状态的到来而逐步降低，当上限降到只有正常状态的三分之一、甚至是四分之一的时候，你的每一个动作都将性命攸关。个人消耗用的武器、弹药、药品倒是很容易在探索过程中获得，但是受制于极为有限的背包容量，你很可能经常不得不在各个稀缺的资源当中做痛苦的取舍。在这种情况下，汽车也就成为了伴你探索的最佳伙伴——它除了能让你更快、更安全地进行探索之外，后备箱还能给你提供额外的资源存储空间。不过话又说回来，汽车本身又需要消耗珍贵的汽油，遭受撞击或者大批丧尸攻击后又存在损毁的风险。假如开着汽车在远离据点的荒郊野外出了事故，接下来的路恐怕反而会更加凶险……

打磨仍需努力

　　如今想要做好一款体量完善的写实风格开放世界游戏已经非常昂贵。《腐烂国度2》肯定价值不菲，但是这个项目所能支配的资源肯定和《光环》、《使命召唤》、《战神》这种级别的游戏存在着巨大差距。而这也就意味着它不可能像这些一线3A游戏一样磨平几乎所有影响游戏流畅体验的瑕疵和毛刺，其受众也因此会相对受限。

　　陡峭的学习曲线是《腐烂国度2》最容易让部分玩家感到不适的地方。游戏有一个完整的教程关卡，但是这个教学关基本上只是聚焦于介绍基本操作。这款游戏真正麻烦的地方在于其繁琐的社区建设、运营、扩张体系，但是其后续的引导远远不足以让普通玩家对其进行足够充分的了解。当然，这种类型的生存游戏本来就应该很复杂，而玩家也理所应当通过亲自摸索来不断拓宽自己的认知水平——但是我在把社区发展引上正轨之前，连续两次都因为缺乏对一些基础信息的了解让整个社区都陷入绝境，以至于最后不得不删档重来。对于耐心不是那么充足的玩家来说，这样的体验非常糟心。

　　游戏在许多最基本的细节层面上也存在着海量问题。以2018年的标准来看，场景和人物的建模已经有些落后于时代，人物和载具移动时的动作也稍显僵硬。PC版上层出不穷的Bug和不怎么走心的优化，则立竿见影地让游戏体验直接降低了一个档次。漂浮在半空中的僵尸层出不穷，有时候NPC会因为莫名其妙刷新在房顶上而无法互动，还有一次我着重培养的一个重要角色因为卡在建模边缘无法动弹最终被丧尸群吞噬……

　　《腐烂国度2》将会登陆Xbox One和Win 10商店，支持Play Anywhere，并加入了Xbox Game Pass。从服务和运营的层面上来说，这款游戏其实诚意十足。不过很可惜，这款游戏和不久前的《盗贼之海》一样，短期内不会支持中文。英文苦手的玩家在购买前还请慎重。

结语

　　以上就是我们对《腐烂国度2》单人游玩部分的看法。和初代作品相比，《腐烂国度2》在各方面都变得更充实、更细致，但是由于缺乏玩法层面上的突破和创新，它在本质上更像是一部"守成之作"。再加上它在细节上仍然存在海量欠打磨的瑕疵，《腐烂国度2》在2018年这个时间点上恐怕反而没有初代作品刚发售时那么惊艳。

　　当然，线上功能是这部新作最重要的特性之一，而且许多任务、关卡在多人合作游玩的状态下，很可能会发生戏剧性的体验变化。在游戏正式发售后，我们会对游戏的多人线上功能进行深入体验，到时候我们对《腐烂国度2》的最终评价和评分有可能也会发生变化，还请继续关注。

作者：不倒翁蜀黍

传送门：《腐烂国度2》临时评测7.5分作为半价游戏，它挺靠谱 _ 游民星空 GamerSky.com

来源：知乎 www.zhihu.com
作者：战术大米

【知乎日报】千万用户的选择，做朋友圈里的新鲜事分享大牛。点击下载

订阅：博文 (Atom)