1,2,4,8,16……数列的下一项是什么？

【引子】


小时候，有一类数学题总是让我们抓狂，这类题目叫做「找规律填数」。这类题之所以让人觉得困难，是因为题目常常稀奇古怪，让我们猜不到出题者的意图。


比如，随便给你出两道题：

  • 9，61，__，63，94，46
  • 26，16，__，68，88

你会做吗？[注1]


好了，先把这种奇奇怪怪的题目搁一边，我来给你出一道看起来「正常」一点的题目：

  • 1，2，4，8，16，__

相信看了这道题，你会会心一笑：这题简单，2 的幂我都背过很多遍了，下一项显然是 32。


可是，谁告诉你这就一定是一个等比数列呢？为什么不能是由 多项式 组成的数列？


【1】用多项式方程解数列通项


如果你学过初中数学，你一定知道，两个点可以确定一条直线，三个不共线的点可以确定一条抛物线；如果你又在大学里学过一点线性代数，你也一定知道，在大多数情况下，平面上的 n 个点可以用一个 n-1 次函数准确地拟合出来。[注2]


那么，针对 1，2，4，8，16…… 这个数列，我们已经有了 5 项，于是我们可以用一个 4 次函数来拟合，即：

y=f(x)=a_{4}x^{4}+a_{3}x^{3}+a_{2}x^{2}+a_{1}x+a_{0}

带入 x = 1，2，3，4，5 的情形，我们有：

  • a_{4}+a_{3}+a_{2}+a_{1}+a_{0}=1
  • 16a_{4}+8a_{3}+4a_{2}+2a_{1}+a_{0}=2
  • 81a_{4}+27a_{3}+9a_{2}+3a_{1}+a_{0}=4
  • 256a_{4}+64a_{3}+16a_{2}+4a_{1}+a_{0}=8
  • 625a_{4}+125a_{3}+25a_{2}+5a_{1}+a_{0}=16

这是一个四元一次方程，用传统的消元法不太好解，用 克莱姆法则 解方程组运算会更通用一点，最后得到的解是： a_{4}=\frac{1}{24}，a_{3}=-\frac{1}{4}，a_{2}=\frac{23}{24}，a_{1}=-\frac{3}{4}，a_{0}=1 。

于是数列的通项公式是： f(n)=\frac{1}{24}(n^{4}-6n^{3}+23n^{2}-18n+24)

在这个通项公式下，数列的第 6 项当然就不是 32 了，它是 —— 31。


这不禁让人觉得有些诡异，主要有两点：① 在系数都不是整数的情况下，第 6 项竟然还是一个整数；② 这个整数距离 2 的 5 次幂竟然只差了 1。


【2】拉格朗日插值法


上面我们用解方程的方法推出了数列的第 6 项，但要涉及高阶的行列式运算，不免有些麻烦，其实，还有一种更为直观的方法，叫做 拉格朗日插值法。


拉格朗日插值法的表达式是：

  • 定义： l_{i}(x)={\prod_{j=1,j\ne i}^{n}}\frac{x-x_{j}}{x_{i}-x_{j}} ①
  • y=f(x)=\sum_{i=1}^{n}{f(x_{i})}l_{i}(x)=\sum_{i=1}^{n}f(x_{i}){\prod_{j=1,j\ne i}^{n}}\frac{x-x_{j}}{x_{i}-x_{j}} ②

这么看公式可能不太直观。稍微解释一下：从式 ① 中我们可以发现，对于我们已经有对应值的 x_{j} ，当 j = i 时， l_{i}(x)=1；当 j ≠ i 时， l_{i}(x)=0 。这个性质使得当 i = 1，2，……，n 时， y=f(x_{i}) 都能成立，故式 ② 也成立。

现在我们已经知道了 f(1)=1;f(2)=2;f(3)=4;f(4)=8;f(5)=16 ，带入式 ①

  • l_{1}(x)=\frac{(x-2)(x-3)(x-4)(x-5)}{(1-2)(1-3)(1-4)(1-5)}=\frac{1}{24}(x-2)(x-3)(x-4)(x-5)
  • l_{2}(x)=\frac{(x-1)(x-3)(x-4)(x-5)}{(2-1)(2-3)(2-4)(2-5)}=-\frac{1}{6}(x-1)(x-3)(x-4)(x-5)
  • l_{3}(x)=\frac{(x-1)(x-2)(x-4)(x-5)}{(3-1)(3-2)(3-4)(3-5)}=\frac{1}{4}(x-1)(x-2)(x-4)(x-5)
  • l_{4}(x)=\frac{(x-1)(x-2)(x-3)(x-5)}{(4-1)(4-2)(4-3)(4-5)}=-\frac{1}{6}(x-1)(x-2)(x-3)(x-5)
  • l_{5}(x)=\frac{(x-1)(x-2)(x-3)(x-4)}{(5-1)(5-2)(5-3)(5-4)}=\frac{1}{24}(x-1)(x-2)(x-3)(x-4)

再带入式 ②， y=f(x)=\sum_{i=1}^{5}{f(x_{i})}l_{i}(x)=\frac{1}{24}(n^{4}-6n^{3}+23n^{2}-18n+24)

这样我们同样得到了数列的通项公式，而且实际上我们可以不用合并同类项，从而规避复杂的行列式计算，使结果更加直观。


拉格朗日插值法告诉我们一个道理：如果我们设定 n=6，无论 f(6) 等于多少，我们都可以迅速得到通项公式（最高为 5 次），所以，理论上来说，如果不限定多项式的最高次幂，数列的第 6 项可以是任何数！不过，如果限定多项式的最高为 4 次，那么数列的第 6 项则是确定的，那就是 31。


【3】数列在几何中的现实意义


看到这里，你也许会有疑问：文章极力说明数列 1,2,4,8,16,…… 的第 6 项其实可以是 31， 但文章也提到，如果不限定多项式的幂，数列的第 6 项可以是任何数，那么，第 6 项是 31 的现实意义是什么呢？


有意义的。因为昨天我收到了这样一封私信：

问题很简单：圆上的 n 个点两两相连，最多可以把圆分成几个部分？


显然 n 为 1~5 的时候，答案分别是 1，2，4，8，16：

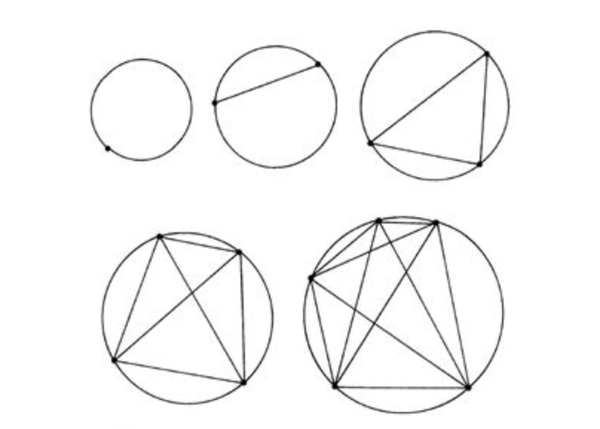
看起来，n=6 的时候，应该是 32 个部分才对，但实际上并不是。


该怎么解这个问题呢？我的解法是这样的：

  • 第一步：把圆上的相邻两个点都连上，成为一个凸 n 边形，于是圆被分成了 n+1 部分；
  • 第二步：连接圆内的点，每个点都可以连出 n-3 条线，于是共连上了 \frac{1}{2}n(n-3) 条线，每条线都至少可以让圆多 1 部分，于是多出了 \frac{1}{2}n(n-3) 部分；
  • 第三步：每次有连线和另一条线相交，圆会多出 1 个部分，因为两条线相交需要有 4 个点，所以理论上最多有 C_{n}^{4}=\frac{1}{24}n(n-1)(n-2)(n-3) 个交点。

综上，对于 n 个圆上的点，圆最多可以被分成的部分数为：

f(n)=n+1+\frac{1}{2}n(n-3)+\frac{1}{24}n(n-1)(n-2)(n-3)=\frac{1}{24}(n^{4}-6n^{3}+23n^{2}-18n+24)


这个答案和之前那个数列的通项公式一模一样！ 所以，n=6 时，答案显然就是 31 了。


这是巧合吗？不，当多项式的前 5 项是 1，2，4，8，16 并且最高次数为 4 时，这个结果已经被注定啦！ [注3]


————————————


注释：

[1] 这两道数列题的答案分别是 52 和 06；第一道：将数列每一项的数字逆序写，是完全平方数；第二道：倒过来看这些数字，分别是 88~92。

[2] 平面上的 n 个点可以用一个 n-1 次函数准确地拟合出来的充要条件是：它的系数矩阵是满秩的。

[3] 这个数列被 OEIS 收录，参见：A000127 - OEIS。



来源：知乎 www.zhihu.com
作者：曾加

【知乎日报】千万用户的选择，做朋友圈里的新鲜事分享大牛。 点击下载
时间：

没有评论:

发表评论

订阅： 博文评论 (Atom)