注:本文首发于公众号「|折枝|」,关注complex-zyb,为**折枝
一
「吃鸡太难了」
前几天,同学找我吃鸡。不出所料,很快就成盒了。这个游戏对于我来说,就是一个「到底死在哪」的游戏。
所以啊,吃鸡是不可能吃鸡的了,这辈子都吃不到鸡,枪又打不准,连队友都打不到,只有靠良好的心态,才能维持下去。
更重要的是,天天吃鸡,荒废学术,让我不胜惶恐。我就开始想,能不能研究一下,如何科学吃鸡?
所以,我就拿出了我的老本行,用Mathematica来研究一下,有什么可以科学吃鸡的方法。吃一次鸡可能是运气,吃两次、三次,可能就是科学了。
幸运的是,Kaggle上已经有了PUBG的数据集,一共有72万次的击杀数据,解压之后,大约有20多G的数据。

里面的信息还是非常丰富的,包括击杀/被杀玩家的位置、原因(武器、车辆)、时间、排名等信息,用工具分析分析,说不定还有可能吃到鸡呢。
前面说了,数据集非常大,单个的CSV文件就已经有几个G的大小了,所以直接用Mathematica的Import函数肯定是作死了,系统直接崩掉。所以这里我用底层的文件流来一行行的输入数据,读取之后立即处理,释放内存,这样才可以读取数据。
下面的代码提供了ImportFirst函数,可以读取CSV文件的前N行,输入是一个文件流对象:
ImportFirst[stream_,type_,n_]:=ImportString[StringRiffle[Table[ReadLine[stream],{n}],"\n"],type] 二
拿到数据,就可以做一些分析了。我一共找到了吃鸡中的三个「秘密」,在这里与大家分享一下。
1、 「死角」的作用有多大?

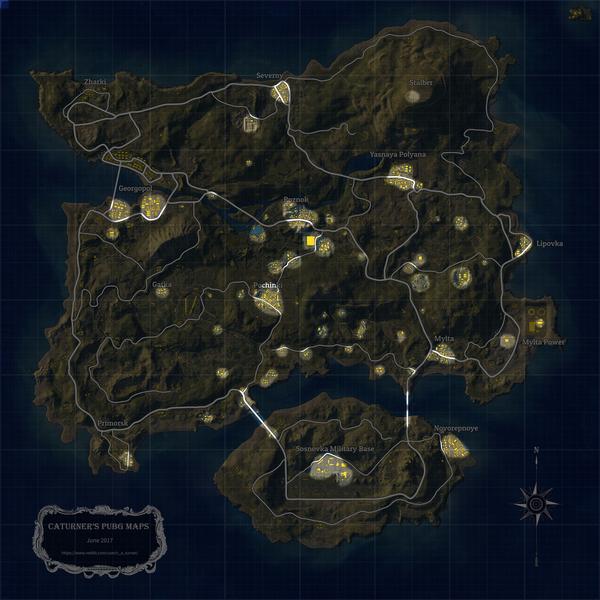
我们都知道,在游戏中要不被人看到,就要利用地形。比如上图中,若要悄悄摸到房子下,可能橙色的路线就比较好,因为相对于窗户来说,其角度非常刁钻,是一个死角。但是,
死角的作用有多大呢?
口说无凭,我们要科学吃鸡,就得做实验。
数据集中,有两个数据可以拿出来研究:击杀者的位置,以及被击杀者的位置。
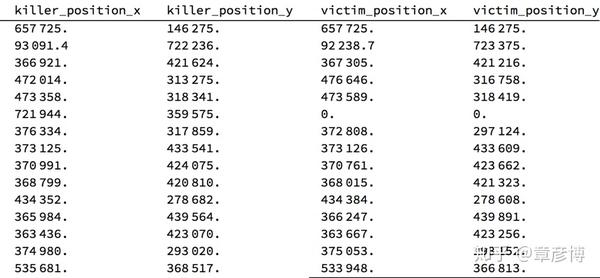
使用这些数据,就可以很容易的计算出角度,如果角度在某些方位上,出现概率有峰值的话,就可以印证我的猜想:死角的确有用。
角度的计算非常容易, 。
我将数据都代入了上面的公式,得到了一个惊人的结果(图中离原点越远,表示这个角度击杀的概率越高):
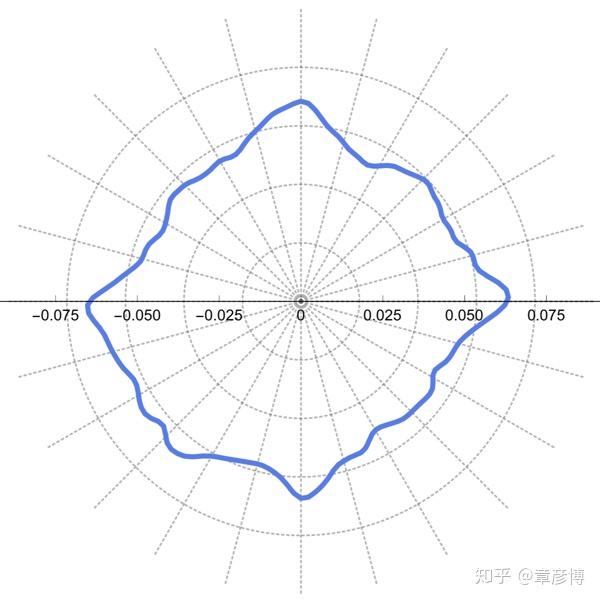
一个近似的正方形!旋转了45度角。这太令人惊讶了,不只在于有四个「死亡角度」,还在于其结构居然如此规整!
这张图意味着什么呢?它意味着:
东南西北四角的击杀概率很高,而四角之间的几个方向,也就是房间里的死角方向,击杀概率很低。

我们反过来,也可以说,在靠近房屋的时候,建议从这四个死角去接近。从统计结果上来看,这几个角度的安全性,比其他方向要高30%!不要小看这30%,如果一局游戏中要三次接近房屋,这就会提高65%的生存率!
2、 地图上的十个「死亡孤岛」
在吃鸡常见的两个地图中,其实还分别暗藏着十个左右的「死亡孤岛」。在这些区域,玩家的死亡数量要明显高于其他位置。如果是吃鸡新手的话,知道这些信息,就可以选择避开这些「是非之地」。
前面提到,我们已经有了击杀、被击杀的位置数据,所以可以很容易的得到击杀位置的分布情况。

首先,可以看看具体的分布情况,这里我使用了Mathematica中的DensityHistogram函数,分别绘制了两个地图的死亡地点分布情况,大图可以在公众号回复「地图」获取下载地址。


图中颜色越红的地方,表示击杀数越多。那有红色标记的地方都不能去了吗?当然不是,我们毕竟要承受一定的风险。所以,可以设定一个阈值:死亡数量高于这个值,就认为是「高危区域」;低于这个值,则认为是安全区域。
所以,我们就得到了第二版的地图——死亡孤岛:
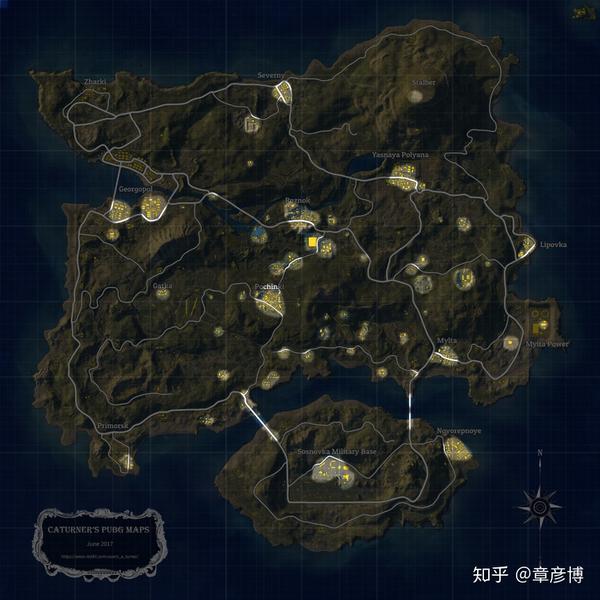

这样,虽然总的信息量减少了,但我们能获得的信息却增加了。这是因为,虽然图像做了简化,但正是这简化的工作,让核心的信息突出了出来。
这里我们可以注意到很多有意思的事情,首先,在海岛地图中,左下角虽然也散落着不少房屋,但却没有出现集中的「死亡岛」。虽然这可能是因为这里的资源比较少,但同样可以作为新手的庇护池。更重要的是,这两张地图,可以作为「玩家密度图」来使用,想苟着,就可以走「暗区」(图中暗色区域);想刚枪,则可以去「明区」。
正因为这些死亡集中的区域,互不相连,就像岛屿一样,所以我称之为「死亡孤岛。」
3、「击杀」是随机的吗?
最后,我们来讨论一个更学术一点的问题:击杀事件是随机的吗?
所谓说「击杀」事件随机,意思就是认为相邻的几次击杀之间没有关联。比如说,可能存在一种机制,使得击杀事件更容易集中起来。举个例子,我在某处淘汰了一个玩家,枪声是否会引来其他玩家,从而提高我被淘汰的几率呢?
数据集中还包含了击杀时间的数据,我们可以以此为切入点,去研究这个问题。
我们首先可以看看击杀时间间隔的分布情况。也就是前后两次击杀的间隔时间,其不同长度的时间,出现概率不同。比如说,可能两次击杀时间间隔为1秒的概率为10%,10秒的概率则可能是1%。
我在对数坐标上绘制了时间间隔的分布图:
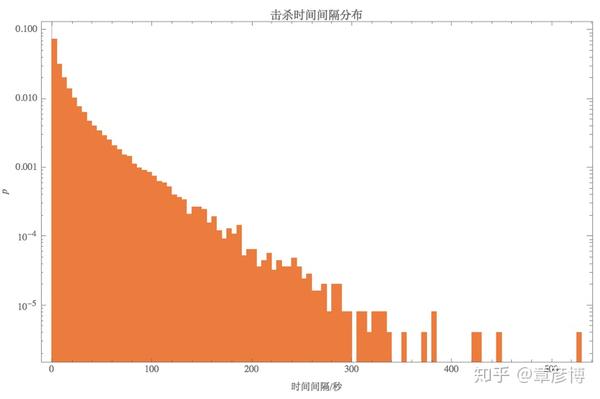
这里,注意到一个非常有意思的现象:在对数坐标下,分布图呈现了近似直线的结构。那么,这意味着什么呢?这意味着击杀事件可能是随机的!
这是因为,如果你使用一个随机生成的序列,每一个事件的发生时间都是随机数,其得到的间隔,其分布就是指数分布!
我们对所有的间隔数据,进行了独立检验:

这里使用Mathematica中的「IndependenceTest」,对间隔数据进行了检验,其结果如下:
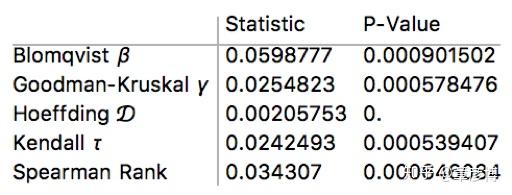
请你关注P-Value这一列,这表示数据前后可能相关的概率。第一列则是各种类型的相关性检验方法,这里不用太过关心。这里的P-Value的值都非常小,意味着在各个假设检验的条件之下,都一致认为,击杀事件都不是随机的!
那么,真的如此吗?我们再看看这张图:

在数值很小的地方,分布其实偏离了指数分布。如果我们提取这一部分的数据,是否会得到不同的结果呢?
检验结果似乎有了很大的变化:
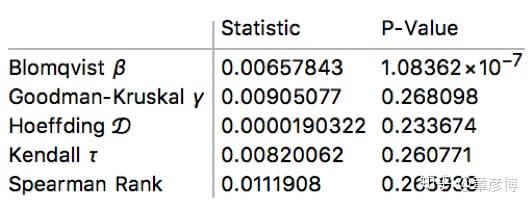
P-Value有了显著的提升(参与检验的序列长度一致),最高达到了26%!这是为什么呢?我们来看看分布,特别是间隔小于20个时间单位的分布情况:
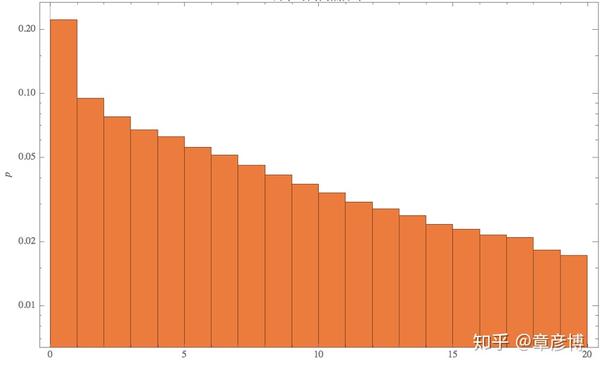
0~1这一段有一个峰值,但在其他位置,仍然保持幂律分布的结构。我们去掉了等于0的数值,结果这里的峰值就没有了。我们再做一下相关性检验:
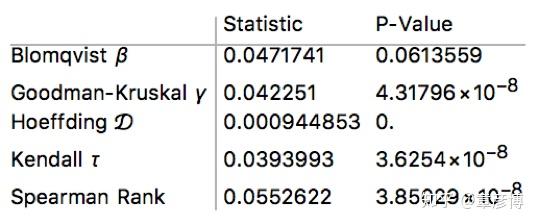
很明显,P-Value大部分都非常小,只不过Blomqvist beta测试超过了0.05的阈值,说明在线性相关方面,独立性还不够显著。所以,我们可以认为
击杀事件不是随机的,虽然间隔分布符合指数分布,但仍然是有很弱的关联的
三
最后,我吃到鸡了吗?
没有。吃鸡是不可能吃鸡的,
数据科学这么好玩,进了里面去,个个都是人才,说话又好听,超喜欢在里面。

最后来打个硬广:
我在集智AI学园开设了系统的Mathematica教程,喜欢数据科学/Mathematica的朋友千万不要错过!
Mathematica基础入门教程往期教程:
章彦博:从1+1到混沌 | Mathematica系列教程·第一集章彦博:一行代码能做什么?|Mathematica十分钟教程章彦博:Mathematica系统教程之·函数可视化·绘图函数通览来源:知乎 www.zhihu.com
作者:知乎用户(登录查看详情)
【知乎日报】千万用户的选择,做朋友圈里的新鲜事分享大牛。 点击下载
没有评论:
发表评论