经典网文分享

实分析Ⅱ|笔记整理（3）——第一章部分习题及解答

大家好！

这一部分选自讲师花了两节课（实际上可能还拖了两节课的堂）讲的第一章的相关习题。它们多半都有一定的难度，很多的步骤都不是"顺其自然"可以想到的，因此可把这一节笔记内的证明思想一样作为积累为以后运用。

注意：这一节的习题主要会使用分析法来叙述，因此不能直接使用在试题或者教科书中。

提供之前的笔记：

我们开始本节的内容。本节是复习章节。

首先是一些集合语言的翻译题。

Problem 1:
试用 $\{x: f_j(x) \ge \frac1k\}$ 表示 $\{x: \overline{\lim_{j \to \infty} }f_j(x) >0 \}$

常规题，从左到右剖析每一个运算的集合意义。

首先我们在第一节介绍了 $\{x: \overline{\lim_{j \to \infty} }f_j(x) >0 \} = \bigcup_{k=1}^{\infty}\{x: \overline{\lim_{j \to \infty}} f_j(x) \ge \frac1k\}$ ，之后要注意函数上极限的定义（数分一中有），就是对一个函数列的上确界取极限，具体一些就是 $\bigcup_{k=1}^{\infty}\{x: \lim _{N \to \infty} \sup _{j \ge N} f_j(x) \ge \frac1k\}$ 。进一步想，如果 $N \to \infty$ 时，它的上确界列依然是 $\ge \frac1k$ 的，那么我在比较小的时候，这个上确界列也依然是满足这个条件的（在小的时候，要取上确界的函数值对象其实变多了，那么上确界的值自然不会减），而另一方面，如果对于每一个都满足这个不等式，那取极限自然也满足条件。根据这个思路我们可以得到它为 $\bigcup_{k=1}^{\infty}\bigcap_{n=1}^{\infty} \{x: \sup _ {j \ge N} f_j(x) \ge \frac1k\}$ 。接下来，如果存在 $j_0 \ge N$ ，使得这个函数的值是 $\ge \frac1k$ 的，那么自然对这个函数列取上确界也是满足条件的。所以进一步可以得到它为 $\bigcup_{k=1}^{\infty} \bigcap_{N=1}^{\infty} \bigcup_{j=N}^{\infty}\{x: f_j(x) \ge \frac1k\}$ 。这就已经完成了我们的构造。

Problem 2:
设 $\lim_{n \to \infty} f_n(x) = \chi _{[a,b] \setminus E}(x),x \in [a,b]$ ，令 $E_n = \{x \in [a,b] \mid f_n(x) \ge \frac12\}$ ，求 $\lim _{n \to \infty}E_n$

这个题的思路也是非同寻常的。首先我们不难猜得答案是 $[a,b] \setminus E$ ，所以要证明集合列的极限是这个答案，就需要考虑一个下极限和一个上极限。我们在第一节说过，一个集合列的上极限是比一个集合列的下极限要"不小"的。所以如果我们说明了这个集合它包含于一个集合列的下极限，却又包含了同样这个集合列的上极限，那么就足够证明结论了。

我们先证明 $[a,b] \setminus E \subset \underline{\lim}\limits_{n \to \infty} E_n$ 。取任意的 $x \in [a,b] \setminus E$ ，那么 $\lim _{n \to \infty} f_n(x)=1$ ，那么根据极限的定义，自然就说明，对于任意的 $\epsilon \in (0,\frac12)$ ，存在一个 $N \in \mathbb{N}^*$ ，使得 $f_n(x) > 1-\epsilon > \frac12 , n \ge N$ 。这就说明了 $x \in E_n,n \ge N$ ，也就是说，我们论证了存在一个满足对于任意的 $n \ge N$ 成立上面的条件，根据集合语言即可知 $x \in \bigcup_{N=1}^{\infty} \bigcap_{n =N}^{\infty}E_n$ 。这就是集合列下极限的定义。

下面，我们再证明 $\overline{\lim _{n \to \infty}}E_n \subset [a,b] \setminus E$ 即可。这里我们考虑对集合取一个补集考虑，意思就是说，只要证明不在右边的集合的元素一定也不在左边集合即可。那么如果 $x \not \in [a,b] \setminus E$ 。这就说明 $x \in E$ ，并且 $\lim_{n \to \infty}f_n(x) =0$ ，那么对于任意的 $\epsilon \in (0,\frac12)$ ，存在，使得 $n \ge N$ 时有 $f(x) < \epsilon <\frac12$ ，这就说明了 $x \not \in E_n$ 。那么自然不可能有 $x \not \in \bigcap_{N=1}^{\infty}\bigcup_{n=N}^{\infty}E_n$ （因为 $x \not \in \bigcup_{n=N}^{\infty}E_n$ ）。也就是它不在集合的上极限中，这就证明了结论。

Problem 3:
$\overline{\lim_{k \to \infty}}\chi_{E_k}(x) = \chi_{\overline{\lim\limits_{k \to \infty}E_k}}(x)$

这个命题是想说两个函数值是恒等的。注意到特征函数只有可能取到0或1，所以分别讨论两种情况自然就可以了。

假设 $\chi_{\overline{\lim\limits_{k \to \infty}E_k}}(x)=1$ ，这就说明 $x \in \bigcap_{N=1}^{\infty}\bigcup_{k=N}^{\infty}E_k$ ，翻译一下就是说，对于任意的 $N \in \mathbb{N^*},\exists k \ge N, s.t. ~x \in E_k$ 。现在我们再看看另一边，注意到函数值的上极限就是 $\lim \sup$ 的意思。那么把我们得到的解释语言翻译为特征函数，就是说，对于任意的 $N \in \mathbb{N^*}$ ， $\sup_{k \ge N}\chi_{E_k}(x)=1$ 。那么由于 $\overline{\lim _{k \to \infty}}\chi_{E_k}(x)=\lim_{N \to \infty}\sup _{k \ge N}\chi_{E_k}(x) =1$ ，所以自然就说明了结论。

假设 $\chi_{\overline{\lim\limits_{k \to \infty}E_k}}(x)=0$ ，那就是 $x \not \in \bigcap_{N=1}^{\infty}\bigcup_{k=N}^{\infty}E_k$ 。把上面的解释语言取反，就是说 $\exists N \in \mathbb{N^*} ~ s.t. ~ x \not \in \bigcup_{k=N}^{\infty}E_k$ 。那么自然对于任意的 $k \ge N, \sup_{k \ge N} \chi_{E_k}(x)=0$ ，这就说明了 $\overline{\lim _{k \to \infty}}\chi_{E_k}(x)=\lim_{N \to \infty}\sup _{k \ge N}\chi_{E_k}(x) =0$ ，也就得到了结论成立。

下面是关于集合是否可数的一些题目。

Problem 4:
设 $E \subset (0,1)$ 是无限集。若从中任意选取不同的数所组成的无穷正项级数总收敛，试证明可数。

首先因为 $E \subset (0,1)$ ，所以如果我们设 $E_n=\{x \in E : \frac1{n+1} \le x < \frac1n\}$ ，那么 $E = \bigcup_{n=1}^{\infty}E_n$ 。然后注意到每一个 E_n 内的元素都是有限个的即可（这是因为如果有一个集合 $E_{n_0}$ 它是无限集，那么取里面的元素就有 $\sum_{n=1}^{\infty}x_n \ge \sum_{n=1}^{\infty}\frac1{n_0}$ 发散），有限个是可数个，可数个可数集合并一下自然还是可数的，这就证明了结论。

对一个集合做"可数的拆分"是一个很重要的证明集合可数的方式。

Problem 5:
设是定义在上的实值函数，且存在常数使得对中任意有限个数 $x_1,x_2,\cdots,x_n$ 有 $|f(x_1)+f(x_2)+\cdots+f(x_n)| \le M$ 。试证明 $E=\{x \in [0,1] : f(x) \ne 0\}$ 是可数集。

事实上，设 $E_n=\{x \in [0,1]: n < |f(x)| \le n+1\}$ , $F_n=\{x \in [0,1] : \frac1{n+1} < |f(x)| \le \frac1n\}$ ，那么 $E=\bigcup_{n=1}^{\infty}(E_n \cup F_n)$ 。同样的思路，现在只需要说明，对于每一个固定的， $E_n \cup F_n$ 都是有限集即可。不妨假设存在 $F_{n_0}$ 是一个无限集，那么根据 $\sum_{k=1}^{M(n_0+1)}f(x_k) > M$ 即可推出矛盾，所以它每一个都是有限集，同理对 E_n 。所以 $E_n \cup F_n$ 每一个都是有限集。可数个并自然是可数集，结论证完。

Problem 6:
设是定义在 $\mathbb{R}$ 上的实值函数。若对于任意的 $x_0 \in \mathbb{R}$ ，都存在 $\delta>0$ ，使得 $|x-x_0| <\delta$ 时， $f(x) \ge f(x_0)$ ，证明 $E=\{y:y=f(x)\}$ 是可数集。

简单分析一下题目，意思就是说，对于任意的 $y \in E$ ，都 $\exists x \in \mathbb{R},~ s.t. ~ f(x)=y$ 。也就是说存在 $\delta_x>0$ ，使得 $\forall x' \in (x-\delta_x,x+\delta_x),f(x') \ge f(x)$ 。那么如何证明可数呢？这里的思路是，构造一个函数定义域内点到函数值的一一映射。

那么因为定义域需要构造成可数的。所以需要用有理数集做一些处理。取 $r_x \in (x-\delta_x,x) \cap \mathbb{Q},R_x \in (x,x+\delta_x) \cap \mathbb{Q}$ 。这样就有 $x \in I_y =(r_x,R_x) \subset (x-\delta_x,x+\delta_x)$ 。

考虑构造映射 $f:E \to \{I_y\}_{y \in E}$ ，那么根据映射的定义，满射是显然的。下面考虑证明它是一个单射。若对于两个元素 $y,y' \in E$ ，有 $I_y \in (r_x,R_x) =(r_{x'},R_{x'})=I_{y'}$ ，那么就有 $x \in (r_x,R_x) \subset (x'-\delta_{x'},x'+\delta_{x'})$ 。这样的话， $y=f(x) \ge f(x') =y'$ （注意一下我们证明开始部分的中间结论）。而证明 $y' \ge y$ 是同理的。也就是说是一个单射。

现在构造出了一一映射，又因为 $\{I_y\}_{y \in E}$ 是有理数的子集，那自然是可数集。结论证完。

Problem 7:
不存在 $\mathbb{R}$ 上的连续函数，其在无理数集 $\mathbb{R} \setminus \mathbb{Q}$ 上是一一映射，而在 $\mathbb{Q}$ 上不是一一映射。

我们假设存在这样的函数，那么自然存在 $a_0,b_0 \in \mathbb{Q}$ ，使得 f(a_0)=f(b_0)=y_0 。令 $E=\{x \in [a_0,b_0]:f(x)=y_0\}$ ，下面的证明重点自然围绕展开。

首先先证明 $\bar E \subsetneq[a_0,b_0]$ 。否则的话，就说明它在内是稠密的，也就是说任意的一个区间都会存在一个点它的函数值是 y_0 。这样的话，利用极限语言可知，对于任意的 $x_1,x_2 \in [a_0,b_0] \setminus \mathbb{Q}$ （既然你要推矛盾，自然要考虑无理数的方向），使得 $x_{k_1} \to x_1,x_{k_2} \to x_2,k \to \infty$ ，其中 $\{x_{k_1}\} \subset E,\{x_{k_2}\} \subset E$ 。由于函数是连续函数，所以可以考虑极限，因此这样的话可以得到 f(x_1)=f(x_2)=y_0 ，这就矛盾了（因为无理数上是一一映射）。

既然这个集合不稠密，那么自然存在 $x_0 \in [a,b] \setminus \bar E$ 与 $\delta_0 >0$ ，使得 $(x_0-\delta_0,x_0+\delta_0) \cap \bar E =\emptyset$ 。因为 $\delta_0$ 是可以任意小的，所以不妨设 $(x_0-\delta_0,x_0+\delta_0) \subset [a_0,b_0]$ 。

现在我们有了一个集合，它内的所有的元素的函数值都不是 y_0 ，那么考虑左右的函数值是 y_0 的相关点，看看是否有更好的结论。设 $a_1=\sup\{x \in [a_0,x_0-\delta_0],f(x)=y_0\}$ , $b_1=\inf\{x \in [x_0+\delta_0,b_0],f(x)=y_0\}$ 。这就说明 f(a_1)=f(b_1)=y_0 ，且对任意的 $x \in (a_1,b_1),f(x) \ne y_0$ 。又因为函数连续，所以要不函数值一直都大于 y_0 ，要不反过来。不妨设是前一种情况，那么存在 $\xi \in [a_1,b_1]$ ，这个点为函数的最大值点。又 $f([a,\xi] \setminus \mathbb{Q}) \subset f([\xi,b_1] \cap \mathbb{Q})$ ，而左边是一个不可数集，右边却可数，这就矛盾了。

重新理一下思路就是，你需要找到一个函数来说明反例，这需要利用区间的不可数性。为了让这样的区间存在，我们必须要说明它不稠密。下面这张图可以说明最后的解释的本质。

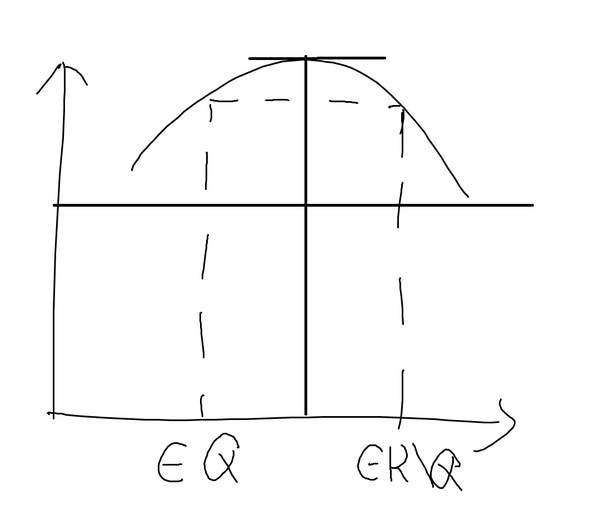
对于每一个具体的区间左边的元素，如果它是有理数，那么与之对应的右边的元素必须是无理数。于是我们构造出了一个一一对应是从可数集到不可数集的，这显然是不可能的。

Problem 8:
若 $E \subset (0,+\infty)$ 中的点不能以数值大小排列，那么 $E' \ne \emptyset$ 。

还是一样，设 $E_n = \{x \in E : n-1 <x \le n\}$ ，那么 $E =\bigcup_{n=1}^{\infty}E_n$ ，那么存在 n_0 使得 $E_{n_0}$ 中的点不能以大小排列，那么就说明它是一个无限集。这样的话，因为每一个都是有限集，所以它必然存在一个极限点（B-W定理），那么自然 $E' \ne \emptyset$ 。

Problem 9:
若 $E \subset \mathbb{R}^2$ 中任意两点间的距离均大于1，那么是可数集。

这种点的距离的题目，我们要证明点可数，自然要把它与有理数联系起来，构造一个一一映射。而开球自然是非常好的方式。

因为有理数集的稠密性可知，对于任意的 $x \in E$ ，取 $r_x \in \mathbb{Q}^2$ ，都可以做到 $x \in B(r_x,\frac14)$ 。先证明 $B(r_x,\frac14) \cap B(r_y,\frac14)=\emptyset$ 。设 $z \in B(r_x,\frac14) \cap B(r_y,\frac14)$ ，那么 $|r_x-r_y| \le |r_x-z|+|r_y-z| <\frac12$ ，但另一方面 $|r_x-r_y| \ge |x-y| -|x-r_x|-|y-r_y| > 1-\frac14-\frac14=\frac12$ ，这就矛盾了。

所以这样的话，每一个就会对应一个独特的 $B(r_x,\frac14)$ ，但是 $\{B(r_x,\frac14)\}$ 是可数的，二者又是对等的，所以自然结论就成立了。

之后的几个题目会与开闭集，覆盖等内容有关。

Problem 10:
设 $F \subset \mathbb{R}^n$ 是闭集，，证明 $E=\{t \in \mathbb{R}^n:\exists x \in F ,s.t. ~ |t-x|=r\}$ 是闭集。

要证明一个集合是闭集，只需要说明 $E' \subset E$ 即可。

注意到，对于任意的 $t \in E'$ ，都存在 $\{t_k\} \subset E$ ，使得 $t_k \to t,k \to \infty$ 。那么由于 $t_k \in E$ ，所以存在 $x_k \in F$ ，使得 |x_k-t_k|=r 。根据 $\{t_k\}$ 可以一一对应得到一个数列 $\{x_k\}$ ，并且由 $\{t_k\}$ 有界可得 $\{x_k\}$ 也有界。那么必然存在收敛子列 $\{x_{k_j}\} \subset \{x_k\}$ ，使得 $x_{k_j} \to x,k_j \to \infty$ ，其中是这个数列的极限。且由于是闭集，可得 $x \in F$ 。那么进一步的，会有 $|x-t| = \lim _{k_j \to \infty}|x_{k_j}-t_{k_j}|=r$ ，这就证明了 $t \in E$ 。结论证完。

Problem 11:
设 $\{F_\alpha\}$ 为 $\mathbb{R}^n$ 中的一族有界闭集，若任取其中有限个 $F_{\alpha_1},F_{\alpha_2},\cdots,F_{\alpha_m}$ 都有 $\bigcap_{i=1}^{m}F_{\alpha_i}\ne \emptyset$ ，证明 $\bigcap_{\alpha}F_\alpha \ne \emptyset$

如果 $\bigcap_{\alpha}F_\alpha = \emptyset$ ，那么挑出其中任何一个 $F_{\alpha_0}$ ，都会有 $F_{\alpha_0} \cap (\bigcap_{\alpha \ne \alpha_0}F_\alpha) \ne \emptyset$ 。也就是 $F_{\alpha_0} \subset (\bigcap_{\alpha \ne \alpha_0}F_\alpha)^c=\bigcup_{\alpha \ne \alpha_0}F_\alpha^c$ 。注意到这是一个开覆盖，所以根据 $F_{\alpha_0}$ 是一个有界闭集可知存在有限的子覆盖 $\{F_{\alpha_i}^c\}_{i=1}^{m}$ ，使得 $F_{\alpha_0} \subset \bigcup_{i=1}^{m}F_{\alpha_i}^c$ 。这就说明 $F_{\alpha_0} \cap (\bigcap_{i=1}^{m}F_{\alpha_i})=\emptyset$ ，这就与题目条件矛盾了。

Problem 12:
设 $K \subset \mathbb{R}^n$ 是有界闭集， $\{B_k\}$ 是的开球覆盖，证明存在 $\epsilon>0$ 使得以中任何一个点为中心， $\epsilon$ 为半径的球一定含于 $\{B_k\}$ 中的一个。

根据覆盖的定义可知，对于任意的 $x \in K$ ，都存在使得 $x \in B_k$ ，也即存在 $\delta_x>0$ ，使得 $B(x,\delta_x) \subset B_k$ ，缩小开球的半径，可以得到 $K \subset \bigcup_{x \in K}B(x,\frac12 \delta_x)$ （事实上，缩不缩小半径，这都一定是对的）。所以存在一个有限的开覆盖，也就是 $K \subset \bigcup_{i=1}^{m}B(x_i,\frac12 \delta_i)$ ，那么再次根据覆盖的定义可得对于任意的 $x \in K$ ，存在 i_0 使得 $x \in B(x_{i_0},\frac12 \delta_{i_0})$ 。那自然存在也就有 $B(x,\frac12 \delta_{i_0}) \subset B(x_{i_0}, \delta_{i_0})=B_{i_0}$ （和第9题构造思路相同），所以这样子只需要令 $\epsilon = \frac12 \min \{\delta_1,\delta_2,\cdots,\delta_m\}$ 即可。

Problem 13:
设有 $\mathbb{R}$ 中的闭集F以及开集列 $\{G_k\}$ 。如果对于每一个都有 $\overline{G_k \cap F} = F$ ，那么有 $\overline {G_0 \cap F} =F$ 。其中 $G_0= \bigcap_{k=1}^{\infty}G_k$ 。

这个命题就相当于是说 G_0 在中稠密。那么要证明它自然只需要说明对于任意的 $x \in F$ 和 $\delta>0$ ，存在 $\xi \in G_0 \cap F$ ，使得 $|x-\xi|<\delta$ 。

从条件出发，取定 $x,\delta$ ，这样就给集合划分了一个范围，我们要去找这个 $\xi$ 。根据 $\overline {G_1 \cap F} =F$ 可知，这个范围内一定都会有 G_1 内的元素，也就是说存在 $x_1 \in G_1 \cap F$ ，使得 $x_1 \in (x-\delta,x+\delta)$ 。那么为了方便讨论，我们进一步做一个限制，取 $\delta_1 \in (0,\min \{\delta,1\})$ ，使得 $[x_1-\delta_1,x_1+\delta_1] \subset (x-\delta,x+\delta) \cap G_1$ （因为 x_1 本身也是开集 G_1 中的元素，所以根据开集的性质，取 $\delta_1$ 非常小的时候这是一定可以做到的）。按照同样的思路，根据 $\overline {G_2 \cap F} = F$ 可以推出来存在 $x_2 \in G_2 \cap F$ ， $\delta_2 \in (0, \min \{\delta_1,\frac12\})$ ，使得 $[x_2-\delta_2,x_2+\delta_2] \subset (x_1-\delta_1,x_1+\delta_1) \cap G_2$ 。

一直推下去就有对于任意的 $k \ge 2$ ，存在 $x_k \in G_k \cap F$ ，使得 $\delta_k \in (0,\min \{\delta_k,\frac1k\})$ ，使得 $[x_k-\delta_k,x_k+\delta_k] \subset (x_{k-1}-\delta_{k-1},x_{k-1}+\delta_{k-1}) \cap G_k$ 。所以说我们就构造出了一个有界递减闭集列 $\{[x_k-\delta_k,x_k+\delta_k]\}$ ，并且会存在 $\xi \in \bigcap_{k=1}^{\infty}[x_k-\delta_k,x_k+\delta_k] \subset \bigcap_{k=1}^{\infty}G_k=G_0$ 。又因为 $\{x_k\} \subset F,x_k \to \xi(k \to \infty)$ ，所以 $\xi \in F$ 。结合 $\xi \in [x_k-\delta_k,x_k+\delta_k] \subset (x-\delta,x+\delta)$ 即可得到结论。

小结

这一节的内容主要是第一节的很多习题（但是不一定覆盖完全了，之后可能会视情况再做增补）。需要提醒的是习题的解答本身也是有很多新奇的思想的，所以不必为做不出习题而感到恐慌，而更多的把它们当作是学习知识的进一步扩充（当然，自然也就是期中考试可能喜欢的内容了）

因为近期我们院就要进行实分析的期中考试了，所以进度会集中在近一周，大家不妨好好期待一下~

感谢大家一直以来的支持，为点赞收藏感谢赞赏的看客比心~~

——————————————————广告——————————————————

本专栏为我的个人专栏，也是我学习笔记的主要生产地。任何笔记都具有著作权，不可随意转载和剽窃。

想要更多方面的知识分享吗？欢迎关注专栏：一个大学生的日常笔记。我鼓励和我相似的同志们投稿于此，增加专栏的多元性，让更多相似的求知者受益~

来源：知乎 www.zhihu.com
作者：刘理

【知乎日报】千万用户的选择，做朋友圈里的新鲜事分享大牛。点击下载

营造二三事——匠与匠心。

营造。匠与匠心。

从图纸设计到最终效果呈现，营造过程格外重要。

传统意义上的营造，是一种身心一致的谋划（营）与建造（造）活动。尤其古典造园活动中，文人指导原则，工匠则负责对建造的研究。

近些年，由于专业的细分，通常讲的营造，往往偏重于造，指的是设计图纸完成后到现场施工完成这个阶段。

营造分离。从教育体系到工作模式，大多数设计师接触现场的机会甚少，与工人基本无交流。工匠的工作就是在现场按图纸浇筑混凝土，他们也几乎没有交流与了解设计理念的契机……这种现行系统导致设计意图不能完全落地，传统意义上追求"自然"的建造法日渐式微。

关于"自然"建造法。

园林景观有其本身的特殊性。

造园四要素：山水、地形、植物和建筑。除了建筑可以用图纸准确表达，其余元素均需要根据现场实际情况做调整。

设计，是空间从无到有的过程。现场营造，则是对空间的理解与深化，如何适宜地建造，是一种"见微知著"的过程。不同工人的理解，指向最终效果的无数种可能性。绿城"三分设计七分营造"的论断，正是基于此。

风华就是这样一个项目。

从立意到图纸，再到现场营造，那些景致背后的情感，以细节来一一还原。

月庭。

树，是最早确定的空间意向。空旷庭院中，有一棵姿态飘逸的树，偏冠。树冠恰恰好在硬质平台上方形成一片浓荫。

有"月庭"的命名，故而有了象征阴晴圆缺的月形蒲团。正好选棵开花的树，取"花前月下"的意境。

还原这个设计推导过程：

风华示范区两进庭院，四处焦点位置，均需特选苗木。设计在图纸阶段，选择2-3种备选品种，后期根据实际情况深化确认。

先根据空间的尺度，确定苗木形态和规格要求。

确定空间意境后，根据施工方提供的开花苗木照片，最终确定品种为八棱海棠。必须是河北怀来的海棠，因为在风口上，树形飘逸，树皮纹理苍劲，正符合项目的定位要求。

怀来海棠，不同于常规印象中椭圆树形。姿态飘逸，树干苍劲。

下图是月庭苗木的演变过程：

左一，是施工方提供的八棱海棠照片。拍摄于两年前。形态、规格与分枝点均符合设计初期设想。是整个项目最先确定的苗木意向。

左二，2016年4月初，怀来县。北方海棠林没有明显标识区分。为了这棵两年前的树，我们在田间反复转悠三个多小时。然而，再见到它，因为炎夏缺水，树枯死大半，唯余顶部数枝绿叶……却是不能再用了。

左三，最终确定的替换苗。胜在满树花芜，姿态轻盈。

左四，长途运输导致的苗木过度修剪。原本能填满整个院子的蔓长枝条，只余两个枝杈。甚为痛心。

最终景观效果。用小朴树替换修剪太过的八棱海棠。依旧月下，不见花前。是关于月庭的一个小遗憾。

营造是这样的过程：以什么姿态去做永远比用什么方法去做要重要的多。接受践行过程中的一切变数，并尽可能的去展现效果。一种"既来之则安之"的哲学态度。

山庭。

纳山势于方寸之间。是山庭的空间立意。

山。最初设想是类似盆景的方式。传统叠石，利用新材料，比如镜面不锈钢，做反差处理？形式创新，还是材料创新？

山庭，在思考和探讨过程中日渐清晰。

我们刻意避开了条石、片岩及叠石等常规做法，而是采用几块泰山石，利用原石外皮起伏的形式，切片、整形、重排。取其自然真趣。

调整是漫长而痛苦的过程。先期对于景石用量的估算不足，原石切片体量偏厚重，现场山势不明显……会让人疑惑甚至怀疑这样的尝试是否可行。我和设计团队，在现场，根据片石的落位继续调整、优化，用炭笔在片石上画出需要修整的轮廓……日复一日。修形和调整落位是一个枯燥而痛苦的过程。我们孜孜不倦。因为热爱。更因为相信。景致，会引领我们，逐渐找到，它原本应该呈现的样子。

调整好片石落位，现场依旧是一片杂乱——建筑垃圾、碎石和包装纸。随着一声"哐当"，凿子应声而断。完成它的最终使命。而片石，已然有了山的起伏……

片岩完成后，进入植物营造阶段。

一棵树，还是两棵树。

最终数量，取决于现场空间尺度，以及选定苗木的树形与规格。

主景树，结合片岩，形成相迎姿态。树冠稍稍高过屋檐，做视线的延伸与引导。而整个庭院空间，沿用国画的留白技法，将植物控制在画面一角。

空间设计确定，树形及规格要求也相应确定：廊高3.6米，故而主景树高度4.5-5米。主景树，不论一棵，还是一组，占据空间约1/3的位置，将大面留白……亦是源自幼时临摹山水画的经验。

选苗：

花木市场的造型松，多偏匠气。它们大多做成迎客松的姿态，枝叶层层分明，如云。美，却缺乏风骨。

我更偏好形态自然的，依稀可见生长于野的不羁。树皮斑驳。松针疯长。

树干宜苍劲，树冠宜飘逸。

逛遍花木市场，终于在墙角看到一棵黑松，疏影横斜，枝干微曲。独株成景。奈何被人捷足先登，早半个月下了定金。

选苗往往如是。得之，我幸。不得，我命。何尝不是中国古人"顺其自然"处世哲学的某种投射。

退求其次，最终选定一棵约5米高的黑松，枝干偏向一侧，苍劲挺拔。只是主干无分枝，冠下稍空。故而在庭院一角增加一株小松，与其呼应……

片岩。苍松。清理完现场，洒上砾石的那一瞬间……忐忑。惊喜。相互交织。呼吸停滞——眼前，景致简洁。意境深远。正是期待中的样子。

我宁愿相信，所有的景致，一直都在。设计，是景致的回归……营造的过程，与其说是设计意图的最终落地，不如说是景致的返乡之路。

作为甲方设计师，我更愿意将自己定位成一名匠人。以贯穿项目始终的探究之心，把"自我"搁置进"空间"，去停留，去感受，去质疑，去推敲。

亲手去实践。

"匠"，是一种态度。执著。一切的可能性。以及，第101种尝试。

从树的朝向，到片石的落位及起伏形态调整……细节，是对意向的还原与升华。

"匠"，亦是一种顺其自然。

营造过程中，有一个现象——越是想表现"自我"，真正的"空间"就越造不出来。我们常常说的匠气，是看似完美的形式下神的缺失。它更像一种对自我的苛刻要求。

触景生情。兴发感动之后，接受不完美的永恒，类似禅的精神。那种自然而深远的空寂。有形的美得以欠缺，却可以有深层，无形之美的追求。

正如那些景致背后……

山庭中一大一小两相宜的黑松。

月庭曾经的"花前"。

水庭，鸡爪槭的前世今生。

……

前世：初进场的鸡爪槭，曾被诟病偏冠、形态太野。

今生：经过疏枝处理，鸡爪槭形态飘逸、洒脱。

现场，有"衣带渐宽终不悔"的执著，更要有包容错误的弹性。

那些完美与不完美之间的纠结……最终落成，与其说是一种妥协，不如说是顺其自然。一种朴素的情感回归。

所有文明的伟大之处都在于其差异丰富的细节。

项目的落成，意味着一个阶段的结束，而另一种意义上的空间营造才刚刚开始。设计师提供了一种暗示多种可能性的场所，但并未决定它。后续使用者的使用和阅读将成为它带来的真正震撼的效果。

原本，风华无边……

来源：知乎 www.zhihu.com
作者：窈慕颜

【知乎日报】千万用户的选择，做朋友圈里的新鲜事分享大牛。点击下载

[读书笔记]意象与心理疗法e——《心理疗法入门》（河合隼雄）第一章

五、置身于意象イメージを生きる

对意象做出简单的解释，反而是有害的。不过，实际上给出无用解释的人并不少。将医学模型带入到心理治疗模型的人，会像"医生治愈病人"一样，认为心理治疗"应该为了治疗而工作"。就像是给病人药物一样，认为给出解释就会有疗效。但是，心理治疗的核心在于来访者潜在的自愈能力。话虽如此，自愈力和承载着无意识的工作有时对自我而言有破坏作用，这点治疗师必须注意。

在这里，倘若重视来访者的自愈力，那么不去干扰这个作业是很重要的。例如，在沙盘治疗中，在这样的工作进行中途一不留神给了个"解释"，莫名与自我产生关联的话，治疗就会停滞下来。故而当治疗的进程开始发生，在一旁不去做解释，静静的关注是很重要的。这在游戏治疗当中也很重要。笔者在欧美提出该主张曾遇到过强烈的反对，但最终也渐渐地取得理解，并得到了国际沙盘疗法学会的全体接受。那些最初反对的人在他们看到成功的临床案例以及亲身体验过之后，也达成了理解。

不过，在（游戏）治疗完成之后，对整个过程进行复盘，治疗师与来访者展开对话时，治疗师会给出自己思考后的"解释"，然后两人对此进行探讨。但不管怎么说，制作沙盘这一过程的"体验"是第一位的。

提到沙盘，那么也说说梦。梦的话，也要不去解释、把做梦的"体验"放在第一位。笔者基本上是这么想的。但是要注意，梦和沙盘还是有诸多不同。

极端点说，不仅做梦，还将梦特意拿出来进行梦的解析工作，并把语言介入其中的必要性在哪里？

本章最早有提到，作为"违背自然"的人类，把各种各样的东西强行重叠在一块。与作为全体的自然建立关系的作业，则在睡眠中进行。这个作业倘若数显意识化，其一部分将会以梦境的方式记忆。因此也可以说，倘若自然的调整作用良好，那么将没有特意做梦或者特意记住梦境的需要。但是，当有问题出现，或者当事人的精神可能存在问题时，为了促进调整作用的良好运转，就有必要分析梦。

关注梦，并且认真地展开对话，意味着多少放下自我的中心作用，活化作为全体的心的工作。在沙盘里，意识也参与其中，一定程度上完成了"作品"，故意识和无意识在其过程中有了适度的合作，在一定范围内得其结果。哪怕不怎么进行言语化工作，来访者也能在很大程度上将其体验收为己用。相对的，做梦的话，由于无意识的工作更强，哪怕将其记忆了下来，对于那一份"作业"，也不如沙盘时的体验强烈。因此，倘若无法好好感受到梦的意义，就很难像沙盘那样在没有解释的情况下继续进程。

为此，分析梦总是必要的。但是到底要进行何种程度谈话才算好，实际上非常困难。这时，最重要的不是如何解释，而是在多大程度上切身体验到梦中无意识的工作。换言之，是否能产生体验。

在日本仓镰时代，有一位名僧法号明惠，少有地将其一生的梦进行了记录。作者研究了他的生平和梦笔记后出版了《明惠夢を生きる（高山寺的夢僧）》。该书认为，明惠并非单纯对梦抱有兴趣，他的人生就是其梦境的真实体验。

再多的描述和解释都是无用的，必须要置身于意象其中（イメージを生きる）。

联系到作者提出过的"带着发现的眼光前行"，德田提出了治疗师的工作与其说是回答来访者的提问，不如说是"对提问进行转化"。

也就是说，心理治疗并非对来访者关于自身的疑问给予最终的答案，而是将看起来无法以一己之力处理的问题转变成看起来可以通过自己身解决的问题。也就是说，目标并非"答案的获得"，而是"问题的转化"。尽管有不少人是奔着消除烦恼来做心理治疗，但是比起将烦恼消除，将其转变成更容易处理的形态才是心理治疗的实际状况。治疗师的作用，或许是陪伴来访者直到其问题成功转变成自身能力可以解决的形态吧。像这样，心理治疗的"答案"其实是新的"问题"，可以说是又一次遇到了两义性了吧。

可以说，心理治疗师在对意象进行言语化的时候，并非给予静止的"答案"，而是提出能够生出新的变化的"提问"。

（第一章内容完）

--------------------------

往期链接：

来源：知乎 www.zhihu.com
作者：知乎用户（登录查看详情）

【知乎日报】千万用户的选择，做朋友圈里的新鲜事分享大牛。点击下载

订阅：博文 (Atom)

实分析Ⅱ|笔记整理（3）——第一章部分习题及解答

小结

营造二三事——匠与匠心。

[读书笔记]意象与心理疗法e——《心理疗法入门》（河合隼雄）第一章

五、置身于意象 イメージを生きる

五、置身于意象イメージを生きる